Непрерывные случайные величины. Понятие о моментах распределения

Понятие о моментах распределения.

Определение 1. Начальным моментом порядка k случайной величины X называют математическое ожидание случайной величины X ^k, где k — натуральное число:

n_k= M (X ^k)

Следовательно, если X имеет распределение

X	х 1	х 2	….	х n
р	p 1	p 2	….	p n

то М(Х) = х^k ₁ р ₁ +х^k₂р₂ +... +х^k_n р _n..

Математическое ожидание и дисперсию случайной величины X можно выразить через начальные моменты порядков 1 и 2

M (X) =n₁ (9.2)

D (X) = М(Х²)- -М ² (Х)= n₂-n₁².

Определение 2. Центральным моментом порядка k случайной величины X называется математическое ожидание величины [Х- М(Х)] ^k:

m_k= [(Х- М(Х)) ^k ].

Из определения центрального момента порядка k, теоремы 9.2 и определения дисперсии следует, что

m₁= [(Х- М(Х))]=0,

m₂= [(Х- М(Х)) ² ]=D(X). (9.3)

Сравнивая соотношения (9.2) и (9.3), получаем

m₂= n₂-n₁²

Пример 9.8. Дискретная случайная величина X задана законом распределения:

X
р	0,4	0,6

Найдем начальные моменты первого, второго порядков и центральный момент второго порядка. Решение. Имеем:

n₁ =М(Х) = 1×0,4 + 3×0,6 = 2,2;

n ₂ = M (X ²) = 1×0,4 + 9×0,6 = 5,8;

m₂=5,8-2,2² =5,8-4,84 = 0,96.

1. Интегральная функция распределения. Для непрерывной случайной величины в отличие от дискретной нельзя построить таблицу распределения. Поэтому непрерывные случайные величины изучают другим способом, который мы сейчас рассмотрим. Пусть X — непрерывная случайная величина с возможными значениями из некоторого интервала (а; b) и х — действительное число. Под выражением Х<х понимается событие «случайная величина Л' приняла значение, меньшее х». Вероятность этого события Р(Х< х) есть некоторая функция переменной х

Р(х) = Р(Х < х).

Определение. Интегральной функцией распределения (или кратко функцией распределения) непрерывной случайной величины X называется функция F(х), равная вероятности того, что X приняла значение, меньшее х:

F(х) = Р(Х < х). (9.4)

Отметим, что функция распределения совершенно также определяется для дискретных случайных величин.

Укажем свойства, которыми обладает функция F(х).

1. 0 £ F(х) £ 1.

Это свойство следует из того, что F(х) есть вероятность.

2. F(х) — неубывающая функция, т.е. если х ₁ < х₂, то F(х_}) £F(х₂).

Доказательство. Предположим, что х ₁ <х₂. Событие «X примет значение, меньшее х ₂» можно представить в виде суммы двух несовместимых событий: «X примет значение, меньшее х ₁ и «X примет значение, удовлетворяющее неравенствам х ₁ £ Х< х ₂». Обозначим вероятности последних двух событий соответственно через Р(Х< х ₁) и Р(х ₁ £Х<х₂). По теореме о вероятности суммы двух несовместимых событий

Р(Х < х₂) = Р(Х< х ₁) + Р(х ₁ £Х<х₂).

откуда с учетом (9.4)

Р(х ₁ £Х<х₂)= F(х₂)- F(х₁). (9.5)

Так как вероятность любого события есть число неотрицательное, то Р(х ₁ £Х<х₂)³ 0 и, значит, F(х₂)³F(х₁).

Формула (9.5) утверждает свойство 3.

5. Вероятность попадания случайной величины Х в полуинтервал [а; b) равна разности между значениями функции распределения в правом и левом концах интервала (а; b):

Р(а£Х<b) = F(b)-F(а). (9.6)

Пример 9.9. Случайная величина X задана функцией распределения

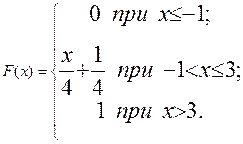
Найдем вероятности того, что в результате испытания X примет значение, принадлежащее полуинтервалу [0; 2).

х

Решение. Так как на полуинтервале [0; 2) F(х) = 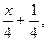то

Р( 0 £Х< 2 ) = F( 2 )-F( 0 ) =

В дальнейшем случайную величину X будем называть непрерывной, если непрерывна ее функция распределения F (х) с непрерывной или кусочно-непрерывной производной.

4. Вероятность того, что непрерывная случайная величина X примет какое-либо заранее заданное значение, равна нулю:

Р(Х = х ₁ ) = 0. (9.7)

Доказательство. Положив в (9.5) х₂ = х ₁ + D х, будем иметь

Р(х ₁ £ X < х ₁ + D х) = F (х ₁ + D х) - F(х ₁). (9.8)

Так как F(х) — непрерывная функция, то, перейдя в (9.8) к пределу при D х ®0, получим искомое равенство (9.7). Из свойства 4 следует свойство 5.

5. Вероятности попадания непрерывной случайной величины в интервал, сегмент и полуинтервал с одними и теми же концами одинаковы

Р(a<X <b) = Р(a£ X £ b) = Р(a£ X <b) = Р(a<X £ b). (9.9)

6. Если возможные значения случайной величины X принад­лежат интервалу (а; b), то 1) F(х) = 0 при х £а; 2) F(х) = 1 при х³b.

Доказательство. 1) Пусть х ₁ £а. Тогда событие Х< х ₁ невозможно, и, следовательно, вероятность его равна нулю.

2) Пусть х ₂ ³ b. Тогда событие X < х₂ достоверно, и, следовательно, вероятность его равна 1.

Следствие. Если возможные значения непрерывной случайной величины расположены на всей числовой оси, то справедливы следующие предельные соотношения:

F(- ¥) = 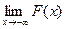=0; F( ¥) = 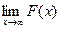= = 1.

2. Дифференциальная функция распределения. Дифференциальной функцией распределения непрерывной случайной величины ДГ(или ее плотностью вероятности) называется функция f(х) равная производной интегральной функции: f(х) = F’(х)

Так как F(х) — неубывающая функция, то f(х) ³ 0 (см. подразд. 3.7, п. 1).

Теорема 9.3. Вероятность попадания непрерывной случайной величины X в интервал (а; b) равна определенному интегралу от дифференциальной функции распределения величины X, взятому в пределах от а до b:

Р(а<Х<b)= 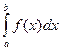. (9.10)

Доказательство. Так как F(х)является первообразной для f(х), то на основании формулы Ньютона— Лейбница (см. подразд. 4.4, п. 2)

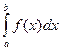=F(b)-F(а). (9.11)

Теперь с учетом соотношений (9.6), (9.9), (9.11) получим искомое равенство.

Из (9.10) следует, что геометрически (см. подразд. 4.3, п. 2) вероятность Р(а<X<b) представляет собой площадь криволинейной трапеции, ограниченной графиком плотности вероятности у = f (х) и отрезками прямых у = 0, х = а и х = b.

Следствие. В частности, если f(х) ) — четная функция и концы интервала симметричны относительно начала координат, то

Р(-а<Х<a)= Р( ½ Х ½ <a)= 2 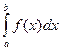(9.12)

Заменяя в формуле (9.11) а на -¥ и b на х, получаем

F(x)-F(- ¥ )= .

откуда, в силу найденного выше следствия (см. п. 1),

F(x)= . (9.13)

Формула (9.13) дает возможность отыскать интегральную функцию распределения F(x) по ее плотности вероятности.

Отметим, что из формулы (9.13) и из только что отмеченного следствия вытекает, что

=1 (9.14)

Пример 9.10. Задана плотность вероятности случайной величины X

f(x)= 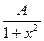(- ¥< x < +¥)

Требуется найти коэффициент А, функцию распределения F(х) и вероятность попадания случайной величины Х винтервал (0; 1).

Решение. Коэффициент А найдем, воспользовавшись соотношением (9.14). Так как

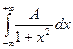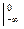= = + = A arctg x + A arctg x =

= A arctg (+¥)- A arctg (-¥)= Аp,

то Аp = 1, откуда А = 1/ p.

Применяя формулу (9.13), получаем функцию распределения F(х):

F(х) = = A arctg x = [ arctg x- arctg (-¥)]=

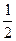== + arctg x.

Наконец, формулы (9.6) и (9.9) с учетом найденной функции F(х) дают

P (0< x < 1)= F( 1 ) - F( 0 ) = .

Дата добавления: 2014-11-29