
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Типовые задачи по вычислению пределов
|
|
|
|
.
Опр. 6 Бесконечно малое, называется низшего порядка по отношению к бесконечно малому, если
МИРОВАЯ ЭКОНОМИКА
Пособие по подготовке к тестированию (краткий курс лекций, вопросы к тестам, вопросы к зачету, планы семинарских занятий) для студентов заочного отделения всех специальностей
Авторы-составители: Ксензова Валентина Эдуардовна
Крижановская Елена Владимировна
Санчук Вячеслав Антонович
Чернявский Михаил Радиславович
Савчук Ирина Алексеевна
Новиков Николай Дмитриевич
Редактор
Корректор
Компьютерная верстка
Сдано в набор Подписано в печать
Формат 60×84 1/16. Бумага тип. №1. Гарнитура Таймс.
Усл. печ. л. Уч.-изд. л. Тираж экз.
Заказ № Цена договорная.
УО «Белорусский торгово-экономический университет
потребительской кооперации»
Лицензия ЛВ № 111 от 21. 01.02.
246029, г.Гомель, просп. Октября, 50.
Отпечатано на ризографе
УО «Белорусский торгово-экономический университет
потребительской кооперации»
Лицензия ЛВ № 112 от 10.01.02.
246029, г. Гомель, просп. Октября, 50.
[1] А. Печчеи Человеческие качества. – М.: Прогесс. 1985. с.35
Пример:
 ;
;
бесконечно малое – 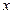 .
.
1. 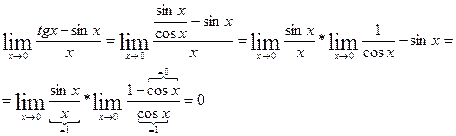
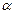 – высшего порядка, чем
– высшего порядка, чем 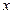 .
.
Какого же порядка???
2. 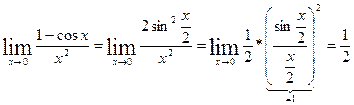 .
.
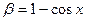 – имеет 2-й порядок по отношению к
– имеет 2-й порядок по отношению к 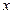 .
.
3. 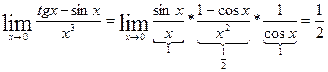 .
.
Следовательно бесконечно малое – 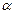 , имеет 3-й порядок малости по отношению к
, имеет 3-й порядок малости по отношению к 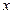 .
.
ТЕОРЕМА 1:
Для того чтобы бесконечно малые – 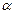 и
и  были эквивалентными, необходимо и достаточно, чтобы разность между ними была бесконечно малой высшего порядка, чем каждая из них в отдельности.
были эквивалентными, необходимо и достаточно, чтобы разность между ними была бесконечно малой высшего порядка, чем каждая из них в отдельности.
Доказательство:
Необходимость:
Дано: 
Требуется доказать: 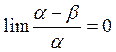
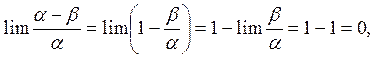 ч.т.д.
ч.т.д.
Достаточность:
Дано: 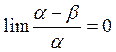
Требуется доказать: 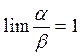
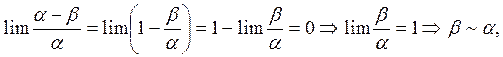 ч.т.д.
ч.т.д.
1) 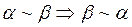
2) 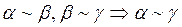
ТЕОРЕМА 2:
При вычислении предела отношений или производной 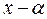 бесконечно малого, каждую из них можно заменить эквивалентной.
бесконечно малого, каждую из них можно заменить эквивалентной.
|
|
|
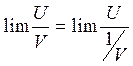
Пусть: 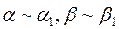 , тогда
, тогда 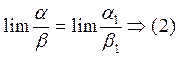 .
.
Доказательство:
Рассмотрим 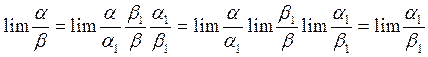 , ч.т.д.
, ч.т.д.
Пример:
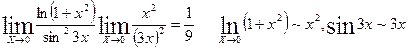
Таблица эквивалентных бесконечно малых:
1. 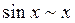
2. 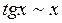
3. 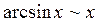
4. 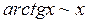
5. 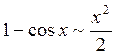
6. 
7. 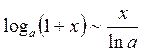
8. 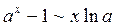
9. 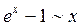
10. 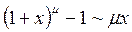
11. 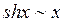
12. 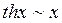
Обобщение теоремы 2
Опр. 7: Две функции 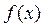 и
и 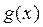 , называются эквивалентными при
, называются эквивалентными при 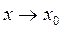 , если
, если 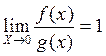
Запись та же самая: 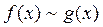
Теорема 2 о эквивалентных бесконечно малых распространяется на случай любых эквивалентных функций.
Формулировка: Если 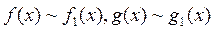 при
при 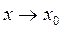 , то:
, то:
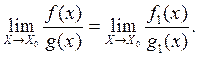
С помощью таблицы эквивалентных бесконечно малых раскрываются различные виды неопределенностей:
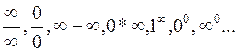
1. 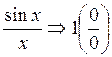
2. 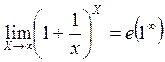
3. 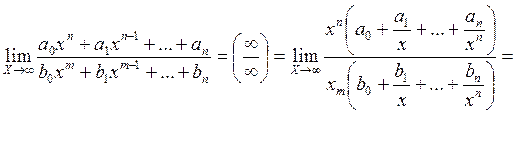
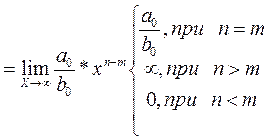
Опр. 8: Если бесконечно малая 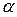 имеет более высокий порядок, чем бесконечно малая
имеет более высокий порядок, чем бесконечно малая 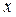 , то принимается запись:
, то принимается запись: 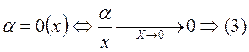 .
.
Формулы для 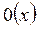 :
:
1. 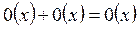
2. 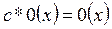
3. 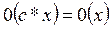
4. 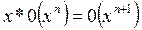
5. 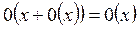
Опр. 8: Если 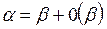 , то бесконечно малая
, то бесконечно малая 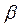 называется главной частью бесконечно малого
называется главной частью бесконечно малого 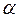 . Т. к.
. Т. к. 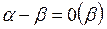 , поэтому
, поэтому 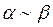 . Каждая из двух этих бесконечно малых является главной частью другой.
. Каждая из двух этих бесконечно малых является главной частью другой.
Если выполняется 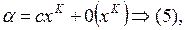 то
то 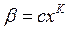 – главная часть
– главная часть 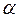 .
.
Таблица эквивалентных бесконечно малых может быть записана в другой форме с использованием символа порядка.
Формула типа 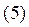 называется асимптот. формулой.
называется асимптот. формулой.
Таблица асимптот. Формул:
1. 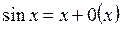
2. 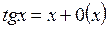
3. 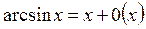
4. 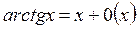
5. 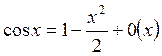
6. 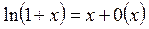
7. 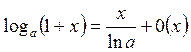
8. 
9. 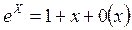
10. 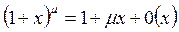
11. 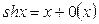
12. 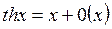
Тезисы:
1. Аналогично сравнению бесконечно малых происходит сравнение бесконечно больших.
2. Сумма бесконечно малых эквивалентна бесконечно малому наинизшего порядка.
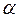 – бесконечно малая величина.
– бесконечно малая величина.
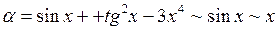
Следовательно: 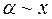 .
.
3. Сумма бесконечно больших эквивалентна бесконечно большому наивысшего порядка роста.
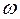 – бесконечно большая величина.
– бесконечно большая величина.
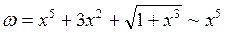
1. При вычислении предела отношения и производной бесконечно малой следует пользоваться таблицей бесконечно малых. Каждую бесконечно малую заменяем более простой эквивалентной бесконечно малой…
2. При вычислении предела с бесконечно малой, в которой встречаются сумма и разность, следует пользоваться таблицей асимптотических формул.
|
|
|
3. При раскрытии неопределённости показателя 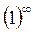 всегда следует прологарифмировать показательное выражение.
всегда следует прологарифмировать показательное выражение.
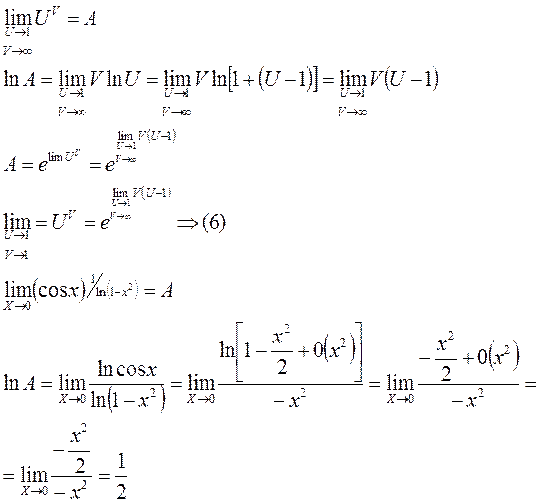
ГЛАВА 2: __________________________________________.
ПАРАГРАФ 1: НЕПРЕРЫВНОСТЬ ФУНКЦИИ.
Понятие о непрерывности функции описывает непрерывные процессы в округе… Непрерывные функции описывают непрерывные процессы.
Будем обозначать: 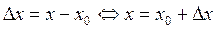 – приращение аргумента.
– приращение аргумента.
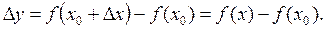 – приращение функции.
– приращение функции.
Опр. 1: Функция 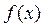 называется непрерывной в точке
называется непрерывной в точке 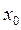 , если она определена в окрестности точки
, если она определена в окрестности точки 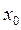 и бесконечно малое приращение аргумента соответствует бесконечно малому приращению функции
и бесконечно малое приращение аргумента соответствует бесконечно малому приращению функции
Под окрестностью точки понимают любую 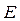 – окрестность этой точки.
– окрестность этой точки.
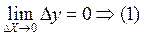
Запишем 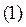 на языке
на языке 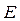 – окрестностей, используя определение предела функции.
– окрестностей, используя определение предела функции.
Опр. 2: Функция 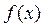 называется непрерывной в точке
называется непрерывной в точке 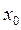 , если она определена в окрестности точки
, если она определена в окрестности точки 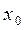 и по любому
и по любому  можно указать
можно указать 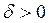 , то при выполнении:
, то при выполнении: 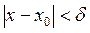 следует:
следует: 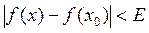
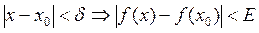
Запишем формулу  ещё в другом виде:
ещё в другом виде:
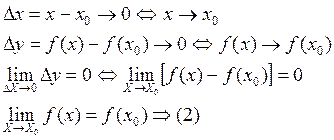
 позволяет сформулировать следующее определение, равносильное предыдущему.
позволяет сформулировать следующее определение, равносильное предыдущему.
Опр. 3: Функция 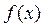 называется непрерывной в точке
называется непрерывной в точке 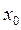 , если она определена в окрестности точки
, если она определена в окрестности точки 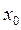 и предел функции равен функции предельного значения аргумента.
и предел функции равен функции предельного значения аргумента.
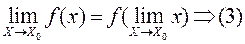
Для непрерывной функции знаки предела и функции можно поменять местами. Запишем уравнение 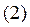 , употребляя пределы с лева и с права. Заметим, что если существует двусторонний предел, то существует оба односторонних предела и они равны между собой, поэтому
, употребляя пределы с лева и с права. Заметим, что если существует двусторонний предел, то существует оба односторонних предела и они равны между собой, поэтому 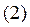 может быть записана в следующей эквивалентной форме:
может быть записана в следующей эквивалентной форме:
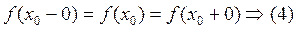
Опр. 4: Функция 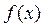 называется непрерывной в точке
называется непрерывной в точке 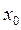 , если она определена в окрестности точки
, если она определена в окрестности точки 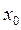 , существуют конечные пределы с лева и с права и выполняется равенство:
, существуют конечные пределы с лева и с права и выполняется равенство: 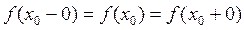 .
.
Пределы с лева и справа равны между собой и равны значению функции в точке.
Опр. 5: Функция 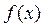 называется непрерывной на промежутке, если она непрерывна в каждой точке промежутка.
называется непрерывной на промежутке, если она непрерывна в каждой точке промежутка.
ПАРАГРАФ 2: ТОЧКИ РАЗРЫВА ФУНКЦИИ.
Опр. 1: Точка 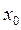 называется точкой разрыва функции
называется точкой разрыва функции 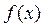 , если нарушается хотя бы одно из условий определения непрерывности функции; используем опр. 4:
, если нарушается хотя бы одно из условий определения непрерывности функции; используем опр. 4:
Нарушение: – Условие:
1. 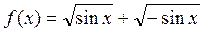
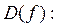 Функция определена в точках, где
Функция определена в точках, где 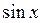 обращается в ноль.
обращается в ноль.
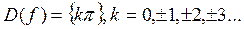
Эта функция разрывна во всех точках области определения функции, т. к. эти точки изолированы без окрестности.
2. Если пределы с лева и с права не являются конечными
|
|
|
|
|
|
|
Дата добавления: 2014-12-16; Просмотров: 388; Нарушение авторских прав?; Мы поможем в написании вашей работы!