
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Бескоалиционные игры
|
|
|
|
Игры двух лиц с произвольной суммой.
В конечной бескоалиционной игре двух игроков (КБИДИ)каждый из них делает один ход – выбирает одну стратегию из имеющегося у него конечного числа стратегий, и после этого он получает свой выигрыш согласно определённым для каждого из них матрицами выигрышей. Другими словами КБИДИ полностью определяется двумя матрицами выигрышей для двух игроков. Поэтому такие игры называются биматричными. Пусть у игрока 1 имеется m стратегий, i = 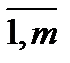 , у игрока 2 имеется n стратегий, j =
, у игрока 2 имеется n стратегий, j = 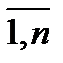 . Выигрыши игроков 1 и 2 соответственно задаются матрицами
. Выигрыши игроков 1 и 2 соответственно задаются матрицами
А = 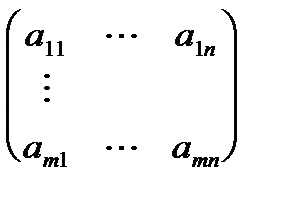 , В =
, В = 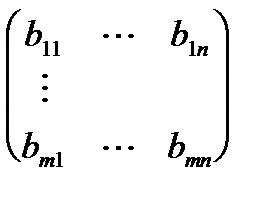
Будем по-прежнему считать полный набор вероятностей x = (x1,..., xm) применения 1 игроком своих чистых стратегий смешанной стратегией игрока 1, и у = (y1,..., yn) – смешанной стратегией игрока 2. тогда средние выигрыши игроков 1 и 2 соответственно равны
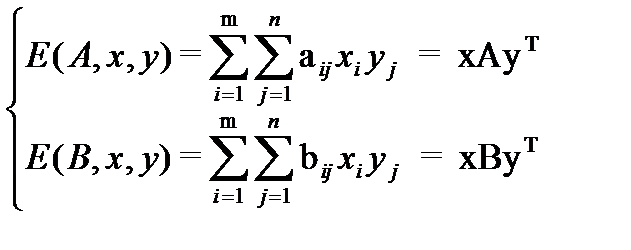
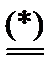
Ситуация равновесия для биматричной игры составляет пару (x,y) таких смешанных стратегий игроков 1 и 2, которые удовлетворяют неравенствам:
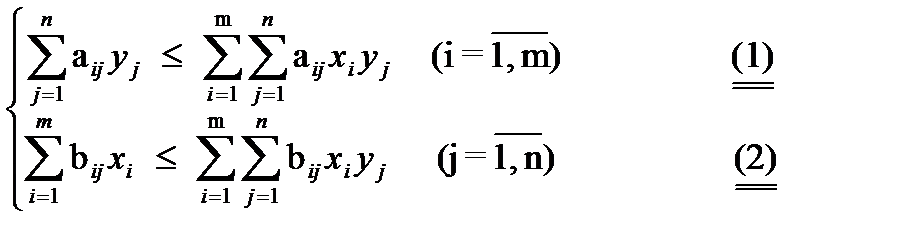
или

Для определения ситуаций равновесия необходимо решить систему неравенств (1) и (2) (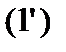 и
и 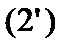 ) относительно неизвестных x = (x1,..., xm) и у = (y1,..., yn) при условиях
) относительно неизвестных x = (x1,..., xm) и у = (y1,..., yn) при условиях
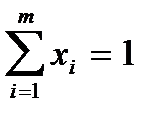 ,
, 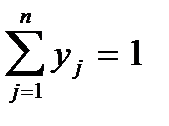 , xi ³ 0 (i =
, xi ³ 0 (i = 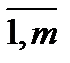 ), yj ³ 0 (j =
), yj ³ 0 (j = 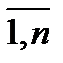 ).
).
Теорема (Нэша). Каждая биматричная игра имеет по крайней мере одну ситуацию равновесия.
В качестве примера рассмотрим случай, когда каждый игрок имеет две чистые стратегии. В этом случае матрицы A и B равны:
A = 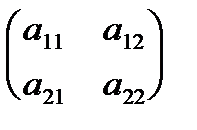 , B =
, B = 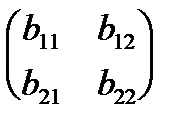 .
.
Смешанные стратегии для игроков 1 и 2 имеют вид:
(x, 1– x), (y, 1– y) 0 £ x £ 1; 0 £ y £ 1,
а средние выигрыши равны:
E1 (A,x,y) = xA 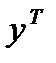 = (x; 1- x)
= (x; 1- x) 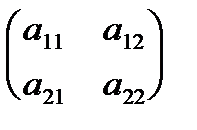
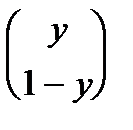 =
=
= (a11 – a12 – a21 + a22) xy + (a12 - a22) x + (a21 - a22) y + a22.
E2 (B,x,y) = xB 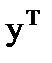 = (x; 1- x)
= (x; 1- x) 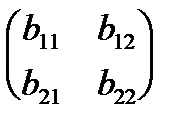
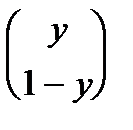 =
=
= (b11 - b12 - b21 + b22) xy + (b12 - b22) x + (b21 - b22) y + b22.
Условия 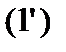 и
и 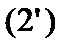 будут выглядеть
будут выглядеть
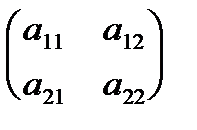
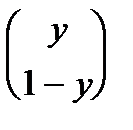 £ E1 (A,x,y),
£ E1 (A,x,y),
|
|
|
(x; 1- x) 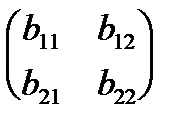 £ E2 (B,x,y),
£ E2 (B,x,y),
или
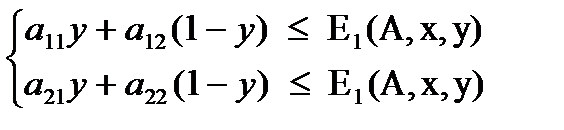
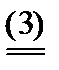
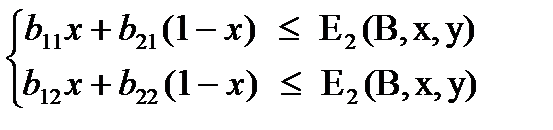
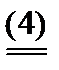
Преобразовав (3) и (4), получим
 (1- x) y +
(1- x) y + 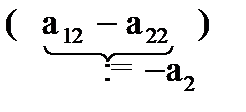 (1- x) £ 0
(1- x) £ 0
(a11 - a12 - a21 + a22) xy + (a12 - a22) x ³ 0
или
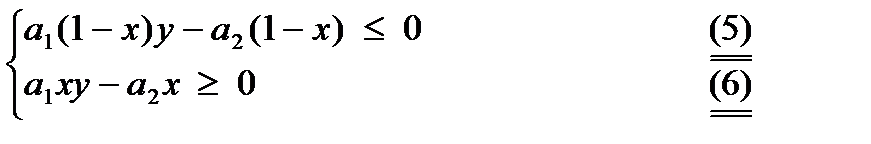
Т. о., множество всех приемлемых стратегий для игрока 1 удовлетворяет условиям (5) и (6), 0 £ x £ 1; 0 £ y £ 1. Чтобы найти x рассмотрим 3 случая:
1. Если x = 0, то (6) справедливо " y, а (5) имеет вид:
a1y - a2 £ 0. 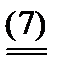
2. Если x = 1, то (5) справедливо " y, а (6) имеет вид:
a1y - a2 ³ 0. 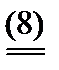
3. Если 0 < x < 1, то (5) разделим на (1 - x), а (6) – на x и получим
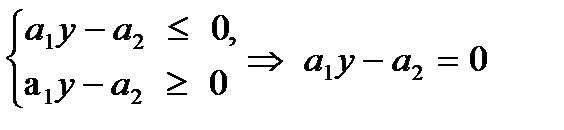
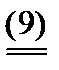
Итак, множество К решений системы (5) – (6) состоит из
1) всех ситуаций вида (0; y), если a1y - a2 £ 0; 0 £ y £ 1;
2) всех ситуаций вида (x; y), если a1y - a2 = 0; 0 < x < 1;
3) всех ситуаций вида (1; y), если a1y - a2 ³ 0; 0 £ y £ 1.
Если a1 = a2 = 0, то решением является x Î[0; 1], y Î[0; 1], т. к. все неравенства (7) – (8) выполняются при всех x и y, т. е. множество приемлемых для игрока 1 ситуаций покрывает весь единичный квадрат.
Если a1 = 0, a2 ¹ 0, то выполняется либо (7), либо (8), и поэтому решением является либо x = 0, либо x =1 при 0 £ y £ 1 (приемлемой стратегии в игре не существует).
Если a1 > 0, то из (7) получаем решение
x = 0; y £ 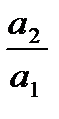 := a,
:= a,
Из (8) следует ещё решение x = 1, y ³ a, из (9) следует ещё решение
0 < x < 1, y = a.
Если a1 < 0, то решение следующее:
x = 0, y ³ a; x = 1, y £ a; 0 < x < 1, y = a.
При этом необходимо учитывать, что дополнительно должно быть
0 £ y £ 1.
Геометрически это выглядит следующим образом:
| · |
1 1 1
a1 >0 a1 >0 a1 >0
a<0 a=0 1< a<1
(x, a)
0 1 x 0 1 x 0 1 x
– ¥ – ¥ – ¥
| · |
| · |
| · |
¥ ¥
1 a1>0 1 a1>0 1 a1< 0
(x, 1) a=1 a >1 (x, a) 0< a<1
(0, b)
x x x
0 – ¥ 1 0 – ¥ 1 0 – ¥ 1
Для игрока 2 исследования аналогичны. Если ввести обозначения
b1:= b11 - b12 - b21 + b22
b2:= b22 - 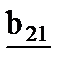
то множество L приемлемых для него ситуаций состоит из:
1) всех ситуаций вида (x, 0), если b1x - b2 < 0; 0 £ x £ 1,
2) всех ситуаций вида (x, y), если b1x - b2 = 0; 0 £ x £ 1; 0 < y < 1,
3) всех ситуаций вида (x, 1), если b1x - b2 > 0; 0 £ x £ 1.
|
|
|
Результаты следующие:
если b1 = b2 = 0, то решение 0 £ x £ 1; 0 £ y £ 1;
если b1 = 0; b2 ¹ 0, то решение либо y = 0, либо y = 1 при 0 £ x £ 1 (приемлемой стратегии в игре не существует);
если b1 > 0, то решения следующие:
y = 0, x < 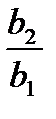 = b; y = 1, x > b; 0 < y < 1; x = b;
= b; y = 1, x > b; 0 < y < 1; x = b;
если b1 < 0, то решения следующие:
y = 0, x > b; y = 1, x < b; 0 < y < 1; x = b
При этом необходимо учитывать, что 0 £ x £ 1.
| · |
| · |
1 1
(b,y) (b,y)
x x
0 1 0 1
b1 > 0 b1 < 0
0 < b < 1 0 < b < 1
Решением игры является пересечение множеств K и L, т.е. те значения x и y, которые являются общими для множеств K и L.
y y
1 1
x x
0 1 0 1
а) б)
При этом зигзаги K и L могут быть не только одинаковой, но и противоположной направленности. В первом случае зигзаги имеют одну точку пересечения, а во-втором – три. Средние выигрыши при этом определяются по формулам (*), если в них подставить полученное решение x и y (рис.а)). Очевидно a входит в смешанную стратегию игрока 2, хотя зависит только от выигрышей 1 игрока; b входит в смешанную стратегию игрока 1, хотя зависит только от выигрышей игрока 2. Сравнение этих результатов с результатами решения матричных игр с нулевой суммой показывает, что a совпадает с оптимальной стратегией игрока 1 в матричной игре с матрицей A, а b – с оптимальной стратегией игрока 2 в матричной игре с матрицей B. Отсюда можно сделать вывод, что равновесная ситуация направляет поведение игроков не только на максимизацию своего выигрыша, сколько на минимизацию выигрыша противника.
С другой стороны, естественно также рассматривать подходящим поведение игроков в конечных бескоалиционных играх, направленное на максимизацию своего выигрыша с учётом максимального противодействия игрока, т.е. подходящей стратегией игрока 1 считать оптимальную смешанную стратегию игрока 1 в матричной игре с матрицей A, а подходящей стратегией игрока 2 считать оптимальную смешанную стратегию игрока 2 в матричной игре с матрицей B, если в ней рассматривать решение с позиций максимизации выигрыша игрока 2, т.е. решать её, как для игрока 1, с матрицей 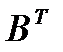 .
.
Пример1. Министерство желает построить один из двух объектов на территории города. Городские власти могут принять предложения министерства или отказать. Министерство – игрок 1 – имеет две стратегии: строить объект 1, строить объект 2. Город – игрок 2 – имеет две стратегии: принять предложение министерства или отказать. Свои действия (стратегии) они применяют независимо друг от друга, и результаты определяются прибылью (выигрышем) согласно следующим матрицам:
|
|
|
A = 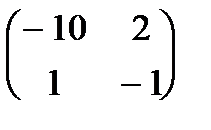 , B =
, B = 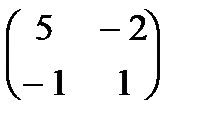
(например: если игроки применяют свои первые стратегии, министерство решает строить 1 объект, а городские власти разрешают его постройку, тогда город получает выигрыш 5 млн, а министерство теряет 10 млн, и т.д.)
Решение. Для этой игры имеем:
a1 = a11 - a12 - a21 + a22 = -10 - 2 - 1 - 1 = -14 < 0,
a2 = a22 - a12 = -1 - 2 = -3,
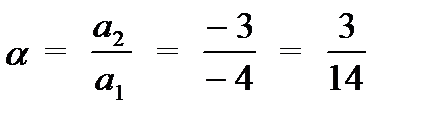 .
.
Так как a1 < 0, то множество решений K имеет следующий вид:
(0, y) при  ;
;
(x, 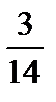 ) при 0 £ x £ 1;
) при 0 £ x £ 1;
(1, y) при 0 £ y £ 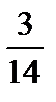 .
.
Для 2 игрока имеем:
b1 = b11 - b12 - b21 + b22 = 5 + 2 + 1 + 1 = 9 > 0,
b2 = b22 - b21 = 1 + 1 = 2,
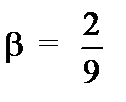 .
.
y
Так как b1 > 0, то множество решений L L
имеет следующий вид:
| C • |
(x; 0), при 0 £ x £ 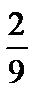 ;
; 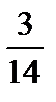
(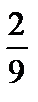 ; y), при 0 £ y £ 1; 0
; y), при 0 £ y £ 1; 0 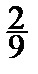 1 x
1 x
(x; 1), при 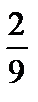 £ x £ 1.
£ x £ 1.
Точка пересечения множеств L и K есть точка C с координатами x = 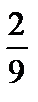 ; y =
; y = 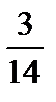 и является соответственно приемлемыми стратегиями министерства и города.
и является соответственно приемлемыми стратегиями министерства и города.
При этом выигрыш соответственно равен
E1 (A,x,y) = (x, 1- x) 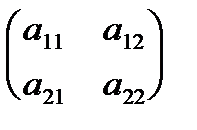
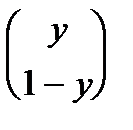 =
=
= 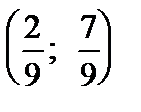
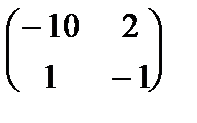
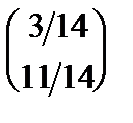 =
= 
E2 (A,x,y) = (x, 1- x) 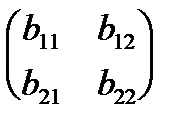
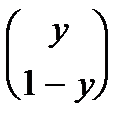 =
= 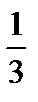
Замечание. Если решить эту игру как матричные игры двух игроков с нулевой суммой, то для игры с матрицей A оптимальные смешанные для 1 игрока и цена игры получаются из решения уравнений
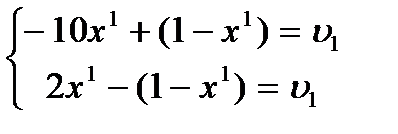
откуда вероятность применения игроком 1 первой стратегии равна 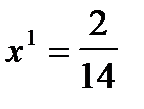 , цена игры –
, цена игры – 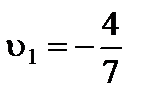 , что совпадает с E1, вероятность применения игроком 2 первой стратегии
, что совпадает с E1, вероятность применения игроком 2 первой стратегии 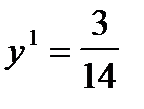 ; для игры с матрицей B оптимальные смешанные стратегии и цена игры для игрока 2 определяются из системы:
; для игры с матрицей B оптимальные смешанные стратегии и цена игры для игрока 2 определяются из системы:
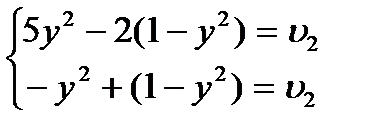
Следовательно, вероятность применения игроком 2 своей стратегии 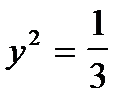 , а игроком 1
, а игроком 1 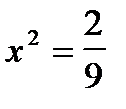 , цена игры
, цена игры 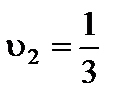 , что совпадает с E2.
, что совпадает с E2.
Таким образом, если каждый из игроков будет применять свои стратегии в этой игре, исходя только из матриц своих выигрышей, то их оптимальные средние выигрыши совпадают с их выигрышами при ситуации равновесия.
Глава 4. КООПЕРАТИВНЫЕ ИГРЫ
|
|
|
Кооперативные игры получаются в тех случаях, когда, в игре n игроков разрешается образовывать определённые коалиции. Обозначим через N множество всех игроков, N ={1, 2,..., n }, а через K – любое его подмножество. Пусть игроки из K договариваются между собой о совместных действиях и, таким образом, образуют одну коалицию. Очевидно, что число таких коалиций, состоящих из r игроков, равно числу сочетаний из n по r, то есть 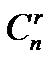 , а число всевозможных коалиций равно
, а число всевозможных коалиций равно
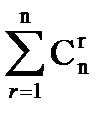 = 2 n – 1.
= 2 n – 1.
Из этой формулы видно, что число всевозможных коалиций значительно растёт в зависимости от числа всех игроков в данной игре. Для исследования этих игр необходимо учитывать все возможные коалиции, и поэтому трудности исследований возрастают с ростом n. Образовав коалицию, множество игроков K действует как один игрок против остальных игроков, и выигрыш этой коалиции зависит от применяемых стратегий каждым из n игроков.
Функция u, ставящая в соответствие каждой коалиции K наибольший, уверенно получаемый его выигрыш u(K), называется характеристической функцией игры. Так, например, для бескоалиционной игры n игроков u(K) может получиться, когда игроки из множества K оптимально действуют как один игрок против остальных N\K игроков, образующих другую коалицию (второй игрок).
Характеристическая функция u называется простой, если она принимает только два значения: 0 и 1. Если характеристическая функция u простая, то коалиции K, для которых u(K)=1, называются выигрывающими, а коалиции K, для которых u(K) = 0, – проигрывающими.
Если в простой характеристической функции u выигрывающими являются те и только те коалиции, которые содержат фиксированную непустую коалицию R, то характеристическая функция u, обозначаемая в этом случае через u R, называется простейшей.
Содержательно простые характеристические функции возникают, например, в условиях голосования, когда коалиция является выигрывающей, если она собирает более половины голосов (простое большинство) или не менее двух третей голосов (квалифицированное большинство).
Более сложным является пример оценки результатов голосования в Совете безопасности ООН, где выигрывающими коалициями являются все коалиции, состоящие из всех пяти постоянных членов Совета плюс ещё хотя бы один непостоянный член, и только они.
Простейшая характеристическая функция появляется, когда в голосующем коллективе имеется некоторое “ядро”, голосующее с соблюдением правила “вето”, а голоса остальных участников оказываются несущественными.
Обозначим через u G характеристическую функцию бескоалиционной игры. Эта функция обладает следующими свойствами:
1) персональность
u G (Æ) = 0,
т.е. коалиция, не содержащая ни одного игрока, ничего не выигрывает;
2) супераддитивность
u G (K È L) ³ u G (K) + u G (L), если K, L Ì N, K Ç L ¹ Æ,
т.е. общий выигрыш коалиции не меньше суммарного выигрыша всех участников коалиции;
3) дополнительность
u G (K) + u(N \ K) = u(N) 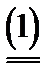
т.е. для бескоалиционной игры с постоянной суммой сумма выигрышей коалиции и остальных игроков должна равняться общей сумме выигрышей всех игроков.
Распределение выигрышей (делёж) игроков должно удовлетворять следующим естественным условиям: если обозначить через xi выигрыш i- го игрока, то, во-первых, должно удовлетворяться условие индивидуальной рациональности
xi ³ u(i), для i ÎN 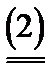
т.е. любой игрок должен получить выигрыш в коалиции не меньше, чем он получил бы, не участвуя в ней (в противном случае он не будет участвовать в коалиции); во-вторых, должно удовлетворяться условие коллективной рациональности
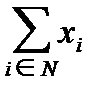 = u(N)
= u(N) 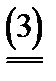
т.е. сумма выигрышей игроков должна соответствовать возможностям (если сумма выигрышей всех игроков меньше, чем u(N), то игрокам незачем вступать в коалицию; если же потребовать, чтобы сумма выигрышей была больше, чем u(N), то это значит, что игроки должны делить между собой сумму большую, чем у них есть).
Таким образом, вектор x = (x1,..., xn), удовлетворяющий условиям индивидуальной и коллективной рациональности, называется дележём в условиях характеристической функции u.
Система { N, u}, состоящая из множества игроков, характеристической функции над этим множеством и множеством дележей, удовлетворяющих соотношениям (2) и (3) в условиях характеристической функции, называется классической кооперативной игрой.
Из этих определений непосредственно вытекает следующая
Теорема. Чтобы вектор x = (x1,..., xn) был дележём в классической кооперативной игре {N, u},
необходимо и достаточно, чтобы
xi = u(i) + ai, (iÎN)
причём
ai ³ 0 (iÎN)
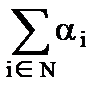 = u(N) –
= u(N) – 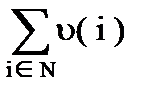
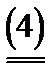
В бескоалиционных играх исход формируется в результате действий тех самых игроков, которые в этой ситуации получают свои выигрыши. Исходом в кооперативной игре является делёж, возникающий не как следствие действия игроков, а как результат их соглашений. Поэтому в кооперативных играх сравниваются не ситуации, как это имеет место в бескоалиционных играх, а дележи, и сравнение это носит более сложный характер.
Кооперативные игры считаются существенными, если для любых коалиций K и L выполняется неравенство
u(K) + u(L) < u(K È L),
т.е. в условии супераддитивности выполняется строгое неравенство. Если же в условии супераддитивности выполняется равенство
u(K) + u(L) = u(K È L),
т.е. выполняется свойство аддитивности, то такие игры называются несущественными.
Справедливы следующие свойства:
1) для того чтобы характеристическая функция была аддитивной (кооперативная игра – несущественной), необходимо и достаточно выполнение следующего равенства:
 = u(N)
= u(N)
2) в несущественной игре имеется только один делёж
{u(1), u(2),..., u(n) };
3) в существенной игре с более чем одним игроком множество дележей бесконечно
(u(1) + a1, u(2) + a2,..., u(n) +a n)
где
a i ³ 0 (i Î N), u(N) —  > 0
> 0
Кооперативная игра с множеством игроков N и характеристической функцией u называется стратегически эквивалентной игрой с тем же множеством игроков и характеристической функцией u1, если найдутся такие к > 0 и произвольные вещественные Ci (iÎN), что для любой коалиции К Ì N имеет место равенство:
u 1 (K) = k u (K) + 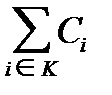
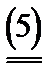
Смысл определения стратегической эквивалентности кооперативных игр (с.э.к.и.) состоит в том что характеристические функции с.э.к.и. отличаются только масштабом измерения выигрышей k и начальным капиталом Ci. Стратегическая эквивалентность кооперативных игр с характеристическими функциями u и u1 обозначается так u~u1. Часто вместо стратегической эквивалентности кооперативных игр говорят о стратегической эквивалентности их характеристических функций.
Справедливы следующие свойства для стратегических эквивалентных игр:
1. Рефлексивность, т.е. каждая характеристическая функция эквивалентна себе u~u.
2. Симметрия, т.е. если u~u1, то u1~u.
3. Транзитивность, т.е. если u~u1 и u1~u2, то u~u2.
Из свойств рефлексивности, симметрии и транзитивности вытекает, что множество всех характеристических функций единственным образом распадается на попарно непересекающиеся классы, которые называются классами стратегической эквивалентности.
Отношение стратегической эквивалентности игр и их характеристических функций переносится на отдельные дележи:
пусть u~u1, т.е. выполняется (5), и x = (x1,..., xn) – дележи в условиях характерис- тической функции u; рассмотрим вектор x1 = (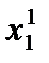 ,...,
,..., 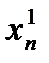 ), где
), где 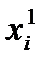 = k xi+Ci; для него выполняется
= k xi+Ci; для него выполняется
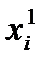 = k xi + Ci ³ k u(i) + Сi = u 1 (i);
= k xi + Ci ³ k u(i) + Сi = u 1 (i);
т.е. выполняется условие индивидуальной рациональности, и
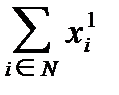 =
= 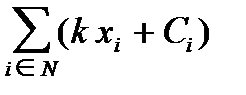 = k
= k 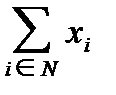 +
+  = k u(N) +
= k u(N) +  = u1(N)
= u1(N)
т.е. выполняется условие коллективной рациональности. Поэтому вектор 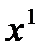 является дележом в условиях u1. Говорят, что делёж x 1 соответствует дележу x при стратегической эквивалентности u~u1.
является дележом в условиях u1. Говорят, что делёж x 1 соответствует дележу x при стратегической эквивалентности u~u1.
Кооперативная игра называется нулевой, если все значения её характеристической функции равны нулю. Содержательное значение нулевой игры состоит в том, что в ней игроки не имеют никакой заинтересованности.
Всякая несущественная игра стратегически эквивалентна нулевой.
Определение. Кооперативная игра с характеристической функцией u имеет (0,1)- редуцированную форму, если выполняются соотношения:
u(i) = 0 (i Î N),
u(N) = 1.
Теорема. Каждая существенная кооперативная игра стратегически эквивалентна одной и только одной игре в (0,1)-редуцированной форме.
Сформулированная теорема показывает, что мы можем выбрать игру в (0,1)-редуцированной форме для представления любого класса эквивалентности игр. Удобство этого выбора состоит в том, что в такой форме значение u(K) непосредственно демонстрирует нам силу коалиции S (т.е. ту дополнительную прибыль, которую получают члены коалиции, образовав её), а все дележи являются вероятностными векторами.
В игре в (0,1)-редуцированной форме дележём является любой вектор x = (x1,..., xn), для которого
xi ³ 0 (i Î N) 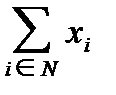 = 1.
= 1.
|
|
|
|
|
Дата добавления: 2014-12-16; Просмотров: 643; Нарушение авторских прав?; Мы поможем в написании вашей работы!