Криві лінії

КРИВІ ЛІНІЇ ТА ПОВЕРХНІ

Криві лінії використовуються в різних галузях науки і техніки. Вони знаходять широке застосування в практиці моделювання, при конструюванні поверхонь різних технічних форм. Вміло підбираючи лінію, дизайнер має можливість надати елегантні та естетично красиві форми виробам, які створює. За допомогою кривих ліній вдається розв’язати багато наукових і інженерних задач, розв’язок яких аналітичним шляхом часто зводиться до використання надзвичайно великого математичного апарату.

Криву лінію можна розглядати, як слід рухомої точки. Прикладом може служити спіраль Архімеда або циліндрична гвинтова лінія.

Криві лінії можна розглядати також як границі поверхні, або як результат взаємного перетину поверхонь. Наприклад, еліпс, який утворений при перетині бокової поверхні прямого кругового циліндра площиною, яка складає з віссю циліндра гострий кут.

Способи утворення кривих ліній можуть бути різними. Одні криві лінії утворюються за певним законом (закономірні криві); утворення іншиих носить емпіричний характер (незакономірні криві лінії). Закономірні криві лінії можуть бути задані графічно і аналітично, тобто рівнянням. Незакономірні криві лінії задаються тільки графічно на кресленні.

Криві лінії в нарисній геометрії задаються своїми проекціями. За двома проекціями можна визначити чи крива лінія плоска чи просторова.

Крива лінія називається плоскою, якщо всі її точки лежать в одній площині; в протилежному випадку – просторовою.

Для дослідження локальної плоскої кривої лінії у довільно вибраній її точці розглядають дотичну та нормаль.

Дотичною лінією t в точці М кривої l називають граничне положення січної КМ, коли точка К вздовж лінії l наближається до точки М. Нормаллю n в точці М до кривої l називається пряма, перпендикулярна до дотичної t в цій точці (рис.7.1).

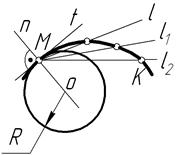
До локальних властивостей кривої відносяться також поняття кривизни. Центр кривизни О для точки М знаходиться на нормалі n до кривої в напрямі її вугнутості. Радіус кола кривизни R в точці М називається радіусом кривизни. Величина К=1/R, обернена до радіуса кривизни, називається кривизною кривої в досліджуваній точці.

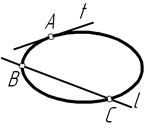
Однією з основних характеристик алгебраїчних плоских кривих ліній є порядок кривої. Він визначається степенем її рівняння, або ж графічно визначається кількістю точок перетину даної кривої лінії прямою лінією. Подана на рисунку 7.2 крива – другого порядку, оскільки пряма l перетинає її у двох різних точках В та С, а в точці А дотична t дотикається до кривої. До плоских кривих замкнутих ліній відноситься лекальна крива еліпс та циркулярна крива – овал, до розімкнутих плоских кривих ліній – евольвента, парабола, гіпербола, спіраль Архімеда, синусоїда та інші.

	Рисунок 7.1 ― Побудова дотичної лінії		Рисунок 7.2.― Крива другого порядку

До закономірних плоских кривих ліній відносяться конічні перерізи (еліпс, гіпербола, парабола), а також евольвента та спіраль Архімеда. Евольвентою називається плоска крива лінія, яку описує точка на прямій лінії, яка без ковзання котиться по нерухомому колу. Нехай задано коло радуса R. Поділимо його на рівну кількість частин (нехай на 8) із точки поділу 1,2,3.....8 проведемо послідовно ряд дотичних ліній, на яких відкладено відповідно одну, дві, три і т.д. частин кола і отримаємо відповідно точки К₁, К₂,...К₈. При послідовному з’єднанні точок К₁, К₂,...К₈ отримаємо евольвенту (рис.7.3). Саме форму евольвенти мають бічні поверхні евольвентних зубчатих передач у деталях машин.

	Рисунок 7.3 ― Евольвента

Другою важливою плоскою кривою лінією є спіраль Архімеда, форма якої широко застосовується в техніці при профілюванні пазів самоцентрувальних кулачкових патронів, кулачкових механізмів тощо. Спіраль Архімеда – це плоска крива, утворена траекторією точки, яка рівномірно рухається по радіусу-вектору і одночасно рівномірно обертається навколо нерухомого центра. Для заданого кроку спіраль Архімеда будують так (рис 7.4). Радіусом рівним кроку спіралі, проводять коло і ділять його на рівну кількість частин (наприклад 8). Перетин концентричних кіл, проведених радіусом 0-1; 0-2; 0-3; і т.д. з променем 0-І; 0-ІІ; 0-ІІІ... визначають точки спіралі Архімеда К₁, К₂, К₃ і т.д.

	Рисунок 7.4 ― Спіраль Архімеда

Відомо, що до точки плоскої кривої можна провести тільки одну нормаль, до точки просторової кривої – безліч нормалей.

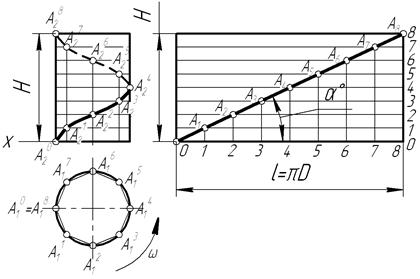
Циліндрична та конічна гвинтова лінії відносяться до просторових кривих. Циліндричну гвинтову лінію утворює траєкторія точки, яка рівномірно рухається по твірній циліндра за умови, що твірна рівномірно обертається навколо осі циліндра в один або другий бік. На рисунку 7.5 зображено круговий циліндр р діаметра D, у якого твірна t рівномірно обертається навколо циліндра проти руху годинникової стрілки. За один оберт твірної t точка А опише на поверхні циліндра коло діаметром D.

Якщо під час повного оберту твірної t, точці А на ній надати рівномірно-поступального руху вздовж твірної вверх, то точка опише на поверхні циліндра просторову криву – циліндричну гвинтову лінію. За повний оберт навколо циліндра точка А піднімається по твірній на величину висоти Н, яка називається ходом. Кут α (рис.7.5б) називається кутом підйому гвинтової лінії. Для побудови проекції гвинтової лінії на розгортці бічної поверхні циліндра коло основи ділять на декілька рівних частин, (у даному випадку на 8); де l=pD. На стільки ж частин ділять хід гвинтової лінії Н. Провівши з точок поділу ряд вертикальних ліній і на перетині з відповідними точками горизонтальних ліній, отримаємо розгортку гвинтової лінії (рис. 7.5б).

Якщо точка переміщається по твірній прямого кругового конуса, а твірна здійснює рівномірний обертовий рух навколо осі конуса, то траєкторією руху точки буде конічна гвинтова лінія. Проекції такої лінії зображені на рисунку 7.6.

Переміщення точки по твірних пропорційні кутовим переміщенням цієї твірної. Для побудови конічної гвинтової лінії ділимо коло основи на рівну кількість частин (наприклад, 8) і відкладаємо ці точки проти руху годинникової стрілки, рухаючи точку рівномірно від основи до вершини на висоту Н. Подальша побудова зрозуміла без додаткових пояснень. Лише зазначимо, що проекція конічної гвинтової лінії на площині проекцій має вигляд згасаючої синусоїди у напрямку знизу догори, а на горизонтальній площині – спіралі Архімеда.

	Рисунок 7.6 ― Конічна гвинтова лінія

Дата добавления: 2014-12-16