Спосіб концентричних сфер

Лінія перетину перетинає сама себе, тобто має спільну точку.

Допоміжні площини проводять у границях між площинами α і β.

Випадок 4 (рис.8.10г). Подвійний дотик; лінія перетину розпадається на дві плоскі криві, які перетинаються.

Допоміжні площини проводять у границях між площинами α ≡ δ і β ≡φ.

Випадок 5 (рис.8.10д). Поверхні не перетинаються.

Іноді для побудови ліній перетину двох кривих поверхонь зручніше використати січні сфери. Принцип допоміжних сферичних перерізів грунтується на тому, що сфера з центром на осі будь-якої поверхні обертання перетинається з нею по колу, яке лежить в площині, перпендикулярній до осі тіла.

Якщо вісь тіла обертання паралельна одній із площин проекцій, тоді коло спроеціюється на дану площину проекцій у вигляді відрізка прямої, яка перпендикулярна до однойменної проекції осі тіла обертання.

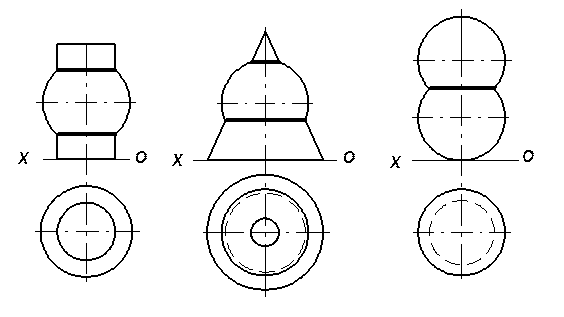На рисунку 8.11а куля перетинається з циліндром, на рис. 8.11б – з конусом, а на рис. 8.11в – взаємний перетин двох сфер.

Задача. Побудувати проекції лінії перетину двох конусів методом січних сфер (рис. 8.12).

Перетинаються два конуси обертання, осі яких розміщені в площині, яка є паралельною до площини p₂. Для пошуку точок, які належать лінії перетину, використаємо допоміжні січні сфери, центри яких лежать на перетині осей конусів (точка О) і кожна із сфер перетинає задані конуси по колах. Проекції кіл, по яких сфера радіусу r перетинає обидва конуси – відрізки прямої.

Характерними точками в даному випадку є точки, які лежать на перетині контурів двох конусів. Це точки 1, 2, 3, 4.

Найменшою сферою буде сфера, яка є вписана в один із конусів і перетинає другий конус. Проводимо коло з центра О₂, взявши його за проекцію кулі. Будуємо проекції кіл, по яких ця куля перетинається з одним із конусів – в, с і дотична до другого конуса, тому перетне по колу а. На перетині цих відрізків дістанемо точки 5₂º6₂ і 7₂º8₂.

Характерні точки 9, 10, 11, 12 знаходимо як точки перетину найближчої і найдальшої твірної конуса з колом, яке одержали від перерізу конуса горизонтальною площиною, проведеною через точку О. Спочатку знаходимо 9₁, 10₁, 11₁, 12₁, а за ними 9₂, 10₂, 11₂, 12₂. Для визначення проміжних точок, що належать лінії перетину, проводимо ще ряд січних сфер різними радіусами, але більшими ніж r_min.

		Рисунок 8.12

На рисунку 8.13 розглянуто особливий випадок застосування способу допоміжних сфер, коли осі заданих поверхонь обертання не перетинаються по осі одного із тіл обертання.

У наведеному прикладі поверхня колового тора перетинається з поверхнею конуса обертання. Тут можна розмірковувати таким чином. Проведемо одне із радіальних перерізів кільця, наприклад, переріз 1-2. Цей переріз являє собою коло, а його фронтальна проекція (1₁-2₂) – відрізок прямої лінії.

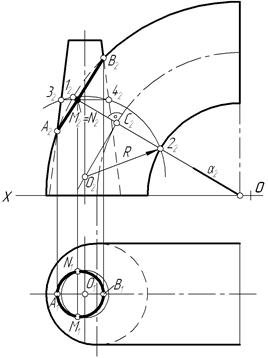Будемо розглядати згаданий переріз, як коловий циліндр безкінечно малої висоти. Тоді вісь циліндра буде перпендикулярна площині циліндра і пройде через його центр (на рис.8.13 фронтальна проекція С₂О₂ осі циліндра), осі циліндра і конуса перетинаються в точці О (фронтальна проекція – О₂).

Тепер будемо вважати, що переріз колом, яке лежить на поверхні сфери кулі з центром у точці О₂. Радіус R кулі, очевидно буде дорівнювати відрізку О₂2₂. Оскільки центр сфери О₂ лежить на осі конуса, лінія перетину цієї сфери з конусом буде колом, фронтальна проекція якого є відрізком прямої лінії 3₂-4₂.

Рисунок 8.13 ― Особливий випадок застосування способу допоміжних сфер

На перетині двох кіл, які належать поверхні однієї сфери, знаходимо точки M і N (M₂ і N₂), горизонтальні проекції M₁ і N₁ точок M і N знаходимо з умови належності їх поверхні конуса (колу 3₂-4₂). Розглянутим методом можна побудувати багато проміжних точок лінії перетину заданих поверхонь.

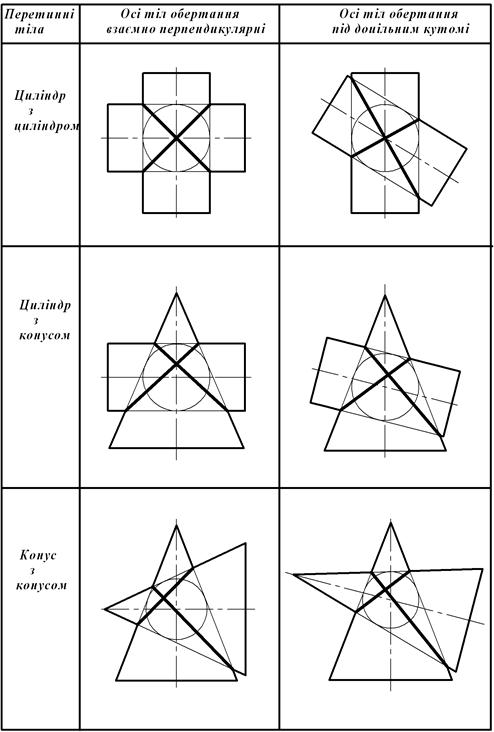
Подвійний дотик. У таблиці 8.1 наведені приклади окремих випадків поверхонь обертання другого порядку, де лінія перетину розпадається на дві плоскі криві, які перетинаються. У кожному з випадків дві поверхні другого порядку, що перетинаються, дотикаються до третьої поверхні кулі (також другого порядку).

За цієї умови має силу теорема Монжа, згідно з якою дві поверхні другого порядку перетинаються і результатом перетину є дві плоскі криві другого порядку, якщо вони описані навколо третьої поверхні другого порядку або вписані в неї.

Відповідно до цієї теореми лінії перетину двох циліндрів, двох конусів або циліндра з конусом, які описані навколо сфери, будуть плоскими кривими – еліпсами, фронтальні проекції яких є відрізками прямих (табл.8.1), на рисунку 8.14 винесеними перерізами є плоскі криві (еліпсів), які отримаємо при перетині циліндра з конусом, якщо останні описані навколо однієї і тієї ж кулі.

	Рисунок 8.14 ― Подвійний дотик ― лінія перетину розпадається на дві плоскі криві, які перетинаються

Таблиця 8.1 – Взаємний перетин двох поверхонь обертання,які описані навколо сфери

Дата добавления: 2014-12-16