Построение обратных задач

Математическую задачу нельзя считать решенной, пока не решена или хотя бы поставлена обратная задача.

Чеботарев Н.Г.

Экспериментально доказано, что наличие упражнений обратной структуры содействует улучшению качества знаний учащихся по математике. Так как:

1. Обратная задача помогает учащемуся извлекать дополнительную информацию, заключающуюся в новых связях между величинами исходной задачи.

2. Решая обратную задачу, учащиеся перестраивают суждения и умозаключения, использованные при решении прямой задачи. При этом они овладевают новыми, более сложными, формами рассуждений.

3. Обратная задача является средством формирования у учащихся способности к переключению на обратный ход мысли – определяющим, исходным элементом математических способностей. (Крутецкий В.А., Эрдниев П.М.).

Дидактическая эффективность приема составления новых задач, обратных данным, определяется:

· возможностью его использования при изучении любых разделов математики;

· вскрытием структурных особенностей (взаимосвязей понятий, тем) изучаемого материала;

· сокращением времени изучения материала;

· осознанным пониманием учащимися изучаемого материала;

· субъектной позицией учащегося. Метод обратных задач приводит ученика к постановке новых проблем, к получению иных разновидностей задач.

Значимость приема построения обратных задач обуславливает необходимость изучения будущими учителями его сути, приобретения опыта составления обратных задач и оперирования (проверка корректности, решение или доказательство) с ними, изучения методики использования приема в обучении математики (в том числе и для составления систем задач).

Суть приема составления обратных задач – при построении обратной задачи меняют местами условие и заключение (требование) исходной задачи.

Приведем пример. Исходная задача – найдите длины медиан _Δ АВС, если его стороны равны a,b,c. Задача, обратная исходной – найдите длины сторон _Δ АВС, если его медианы равны a,b,c.

Поскольку заданных и искомых величин (данных и требований) в задаче может быть несколько, то и так называемая «обратная» задача может быть не одна.

Приведем пример.

Исходная задача – в равнобедренном треугольнике медиана, проведенная к основанию, является высотой и биссектрисой.

Структура задачи: .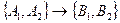

А₁: данный треугольник является равнобедренным. А₂: данный отрезок - медиана, проведенная к основанию.

В₁: данный отрезок - высота. В₂: данный отрезок - биссектриса.

Обратная задача 1: . В равнобедренном треугольнике высота, проведенная к основанию, является медианой и биссектрисой.

Обратная задача 2: . В равнобедренном треугольнике биссектриса, проведенная к основанию, является медианой и высотой.

Обратная задача 3: . Если в треугольнике высота и медиана, проведенные к одной стороне, совпадают, то он является равнобедренным, а высота (медиана) является биссектрисой.

Обратная задача 4: 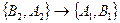. Если в треугольнике биссектриса и медиана, проведенные к одной стороне, совпадают, то он является равнобедренным, а биссектриса (медиана) является высотой.

Обратная задача 5: . Если в треугольнике высота и биссектриса, проведенные к одной стороне, совпадают, то он является равнобедренным, а высота (биссектриса) является медианой.

Выделим особенности построения обратных задач к задачам на доказательство и к задачам на нахождение.

Когда задаче на доказательство соответствует проверка истинности эквиваленции («A тогда и только тогда, когда B», т.е. AÛB), построение обратной задачи не имеет смысла. Существуют математические предложения, представляющие собой высказывания, полученные их некоторых предикатов навешиванием кванторов всеобщности или существования по неизвестным, от которых зависит предикат. Например, нужно доказать истинность высказывания "x $y (x×y = 1), где x,yÎQ\{0}. В этом случае также нет возможности построения обратной задачи в чистом виде.

Поэтому в качестве обратимых задач на доказательство будем рассматривать лишь математические предложения, сформулированное в виде импликации («Если A, то В», т.е. AÞB).

В задаче на нахождение обычно заданы исходные величины (или параметры), от которых зависит получаемый ответ. Когда строим обратную задачу, мы стремимся в качестве одного из исходных данных выбрать ответ, а искомым сделать ранее заданную величину.

Заметим, что строить «обратные» задачи совсем не сложно. Вопрос о необходимости составления обратных задач решается однозначно. Обратные задачи необходимо составлять при изучении любого материала. Другое дело – нужно ли их решать; где решать (в классе или дома); достаточно ли у учащихся знаний для решения сконструированных задач; если теоретической базы не хватает для решения обратной задачи, нужно ли ее формулировать; корректна ли построенная задача? На эти вопросы должна ответить методика использования приема составления обратных задач в обучении математики.

Начнем с обсуждения проблем, возникающих в процессе обратимости задач на доказательство вида AÞB. Построение такой задачи почти не вызывает затруднений, трудности возникают при оценке истинности обратного утверждения BÞA. Например, легко видеть, что утверждение «если в треугольнике две медианы равны, то такой треугольник является равнобедренным», являющееся обратным к утверждению «в равнобедренном треугольнике две медианы равны», истинно и доказать это не трудно. Если же поставить перед собой аналогичный вопрос «известно, что биссектрисы двух углов равнобедренного треугольника равны. Верно ли обратное, что если биссектрисы двух углов треугольника равны, то треугольник равнобедренный?», положительный ответ мы получим не сразу, хотя есть полное ощущение тривиальности доказательства (особенно в свете решения предыдущего вопроса). Оказалось, что найти чисто геометрическое доказательство данного утверждения не так-то легко. Одно из доказательств приведено, например, в книге «Новые встречи с геометрией» Г.С.М. Коксетера и С.Л. Грейтцера.

Если данные обратные утверждения строятся семиклассниками в рамках изучения темы «Свойства равнобедренного треугольника», то для доказательства последнего утверждения у учащихся нет теоретической базы. Однако это не должно стать отказом от составления обратных утверждений. Данную ситуацию можно использовать для формирования потребности в учении. Нехватка знаний – это начало разговора о необходимости в их дальнейшем развитии.

Когда теоретическая база позволяет, условимся не только строить обратные задачи и решать их, но в случае, когда обратное утверждение ложно, попытаемся найти нужные ограничения, чтобы оно стало истинным.

Рассмотрим несколько примеров.

Пример 1. Известно, что в правильной треугольной пирамиде все боковые ребра равны между собой и площади боковых граней совпадают. Верно ли обратное утверждение: если в треугольной пирамиде все боковые ребра равны между собой и площади боковых граней совпадают, то пирамида правильная?

Чтобы опровергнуть обратное утверждение достаточно привести контрпример (синусы плоских углов при вершине пирамиды равны, а сами углы различны).

Усилить дидактическую значимость приема составления обратных задач можно, доопределив обратное утверждение, то есть, составив верную импликацию B₁ÞА для исходной задачи AÞB. В этом случае мы сталкиваемся с ситуацией, когда ищем недостающие или избыточные данные в начальном состоянии предмета задачи. Конечно, не обойдемся без трудностей, которые возникают при формировании условия B₁: тяжело определить, на какие именно элементы стоит накладывать ограничения, да и выбор ограничений слишком неоднозначен.

В нашем примере обратное утверждение будет верным, если в основании пирамиды лежит остроугольный треугольник. Следовательно, обратное утверждение нужно доопределить указанным требованием.

Возможна ситуация, когда утверждение, обратное к очевидному, не является верным, но это не просто доказать [4].

Пример 2. Дан четырехугольник ABCD. Точки K, M, N, L − середины сторон AB, BC, CD и AD соответственно. , , , 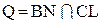. Можно доказать, что если ABCD − параллелограмм, то 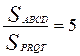. Верно ли обратное утверждение?

Известно, что четырехугольник определяется пятью своими независимыми элементами. Класс параллелограммов высекается из класса четырехугольников двумя соотношениями (любой параллелограмм определяется тремя своими элементами). Данное отношение площадей не задает двух нужных соотношений, т.е. PRQT, вроде бы, не обязан быть параллелограммом. Но, может быть, перед нами частный случай, тем более, что 5 – наименьшее возможное значение этого отношения, то есть при таком построении данным отношением определяется именно параллелограмм. Неудача при подборе контрпримеров только подтолкнет к попытке доказать данное утверждение. Доказать его также не удается, поскольку существуют контрпримеры, но обнаружить их крайне трудно. Например, если A(10;0), B(0;0), C(2;5), D(19;10), то 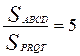, но четырехугольник ABCD − не параллелограмм.

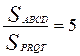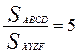После нахождения примера, опровергающего обратное утверждение, можно попытаться найти ограничение, которое приведет к полному описанию параллелограмма. Например, таким ограничением будет набор требований и , где 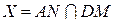, , , 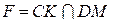. Подробнее о решении обратной задачи и о нахождении указанного ограничения написано в статье Лецко В.А. «Методика организации исследовательской работы старшеклассников в области математики». (См. «Совершенствование процесса обучения математике в условиях модернизации процесса образования» - Волгоград, 2004).

Рассмотрим примеры построения “обратных” задач к вычислительным задачам.

Пример 3. Один из катетов прямоугольного треугольника равен 15 см., а проекция другого катета на гипотенузу равна 16 см. Найти радиус окружности, вписанной в треугольник. Постройте задачу, обратную к данной.

К этой задаче можно построить две обратные задачи. Первая из них, когда за исходные данные берется радиус вписанной окружности и катет (нужно найти проекцию другого катета на гипотенузу), решается так же просто, как и исходная задача. Если же в качестве данных в задаче выбрать радиус вписанной окружности и проекцию катета на гипотенузу, то вычисления, проводимые при нахождении катетов, довольно громоздкие. Построив обратную задачу, нужно оценить, стоит ли использовать составленную задачу при изучении соответствующей темы.

Иногда решение обратной задачи позволяет подобрать наиболее удачные данные для исходной задачи, на что можно обратить внимание учащихся при рассмотрении следующего примера.

Пример 4. Все четыре грани треугольной пирамиды - равные равнобедренные треугольники, длины боковых сторон которых равны . Найдите величину угла при вершине этих треугольников, если объем пирамиды равен 2/3. Постройте задачу, обратную к данной.

При построении и решении обратной задачи обнаружим, что одним из исходных данных должен быть выбран ответ 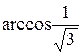(ответ к исходной задаче). Следовательно, можно немного упростить числовые данные: взять величину угла 30° и сторону 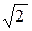. При этом вычисления по ходу решения не особенно изменятся, но исходные числовые данные станут немного проще.

Специфику «сложносоставных» задач – наличие нескольких обратных задач – можно использовать для систематизации учебного материала.

Рассмотрим пример конструирования систем задач к уроку «Пропорциональные отрезки в прямоугольном треугольнике» методом составления обратных задач.

D АВС ~ D АСК (ÐС=ÐАКС, ÐА – общий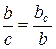) Þ Þ . D АВС ~ D СВК (Ð С=ÐВКС, ÐВ – общий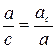) Þ Þ . D АСК ~ D СВК (ÐАКС=ÐВКС, ÐСАК=ÐКСВ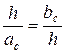) Þ Þ .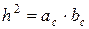

Исходная задача: «Катеты прямоугольного треугольника равны 15 и 8 см. Найдите гипотенузу; высоту, проведенную к гипотенузе; отрезки на которые делит гипотенузу основание высоты».

Составив матрицу условий и заключений, меняя местами данные и искомые величины, получим девять принципиально различных задач по теме.

а	b	c	ac	bc	h
				3,2
					2

Данную таблицу можно заполнять вместе с учениками, показывая пример систематизации знаний, формируя умение составлять обратные задачи.

Сконструированная таким образом система задач позволяет учителю ликвидировать пробелы учебников. Так в учебнике Атанасяна Л.С. «Геометрия 7-9» из сконструированной системы представлены только три типа задач.

Построение обратных задач на уроках математики призвано облегчить учащимся понимание учебного материала.

В пункте «Параллельность прямой и плоскости» учебника Атанасяна Л.С. «Геометрия 10-11» рассматривается взаимно обратные задачи: «Если данная прямая параллельна прямой, по которой пересекаются две плоскости, и не лежит в этих плоскостях, то она параллельна этим плоскостям» и «Если прямая параллельна каждой из двух пересекающихся плоскостей, то она параллельна и их линии пересечения». Первое утверждение приводится в перечне задач к параграфу под номером 25, а второму утверждению присвоен номер 32. При раздельном изучении этих предложений (иногда даже на разных уроках) учащиеся воспринимают задачи как разные, не связанные между собой. Искусство учителя как раз и состоит в умении систематизировать материал и предъявлять его учащимся так, чтобы у них не возникало чувство бессмысленности деятельности по решению задач – сколько не решай, все равно всех не перерешаешь. Построение обратных задач один из способов систематизации учебного материала.

Вопросы и задания

1. Законспектируйте материал о роли и месте обратных задач при обучении математике:

а) Эрдниев П.М. Преподавание математики в школе. М, «Просвещение», 1978. – Ч. I, §2, §6; Ч. III, §1.

б) Дразнин И.Е. Обращение условий планиметрических задач. // Математика в школе. – 2001. – № 8. – с.52-55.

2. Решите данные задачи. Составьте и решите задачи, обратные к данным:

а) Докажите, что средняя линия треугольника параллельна одной из его сторон и равна половине этой стороны.

б) В прямоугольном треугольнике медиана, проведенная к гипотенузе, равна ее половине.

в) Докажите, что биссектриса треугольника делит противоположную сторону на отрезки, пропорциональные прилежащим сторонам треугольника.

г) В равнобедренном треугольнике высоты, проведенные к боковым сторонам, равны.

д) Биссектрисы смежных углов перпендикулярны.

е) Найдите .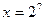

ж) Два крана могут разгрузить баржу за 6 часов. За какое время разгрузит эту баржу первый кран, работая отдельно, если на это ему потребуется на 9 ч меньше, чем второму.

з) Решите уравнение .

3. Подобрать необратимые задачи и добавить некоторые элементы в заключение B (получится утверждение B₁) исходной задачи вида AÞB, чтобы обратное высказывание B₁ÞA стало верным.

4. Приведите контрпримеры, доказывающие ложность следующих предложений:

1) Если сумма делится на 3, то и каждое слагаемое делится на три.

2) Если число делится на каждый сомножитель, то оно делится и на произведение.

3) Четырехугольник, имеющий два прямых угла, является прямоугольником.

4) Если в четырехугольнике диагонали равны, то он является прямоугольником.

5) Биссектриса угла в равнобедренном треугольнике является его медианой и высотой.

6) Равные отрезки, заключенные между параллельными прямыми, параллельны.

5. Методом обращения задачи составьте систему задач по теме «Соотношения между сторонами и углами в прямоугольном треугольнике». Сколько принципиально различных задач? Подберите числовые данные и занесите их в таблицу:

a

b

с

a

b

Опишите фрагмент урока по использованию данной системы задач на уроке.

6. Составьте все обратные задачи к исходной – найдите длины медиан _ΔАВС, если его стороны равны a,b,c. Сколько принципиально различных задач? Решите их. Все ли задачи корректны? Все ли имеют решение? Продумайте методику использования данной системы задач на уроке.

Дата добавления: 2014-12-16