Резонанс напряжений

Известно, что в механической системе резонанс наступает при равенстве собственной частоты колебаний системы и частоты колебаний возмущающей силы, действующей на систему. Колебания механической системы, например колебания маятника, сопровождаются периодическим переходом кинетической энергии в потенциальную и наоборот. При резонансе механической системы малые возмущающие силы могут вызывать большие колебания системы, например большую амплитуду колебаний маятника.

В цепях переменного тока, где есть индуктивность и емкость, могут возникнуть явления резонанса, которые аналогичны явлению резонанса в механической системе. Однако полная аналогия - равенство собственной частоты колебаний электрического контура частоте возмущающей силы (частоте напряжения сети) — возможна не во всех случаях.

В общем случае под резонансом электрической цепи понимают такое состояние цепи, когда ток и напряжение совпадают по фазе, и, следовательно, эквивалентная схема цепи представляет собой активное сопротивление. Такое состояние цепи имеет место при определенном соотношении ее параметров r, L, С, когда резонансная частота цепи равна частоте приложенного к ней напряжения.

Резонанс вэлектрической цепи сопровождается периодическим переходом энергии электрического поля емкости в энергию магнитного поля индуктивности и наоборот.

При резонансе в электрической цепи малые напряжения, приложенные к цепи, могут вызвать значительные токи и напряжения на отдельных ее участках. В цепи, где r, L, С соединены последовательно, может возникнуть резонанс напряжений, а в цепи, где r, L, С соединены параллельно,— резонанс токов.

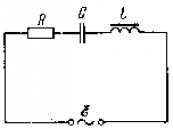
Рассмотрим явление резонанса напряжений на примере цепи рис. 2.11, а.

Как отмечалось, при резонансе ток и напряжение совпадают по фазе, т. е. угол φ = 0. и полное сопротивление цепи равно ее активному сопротивлению.

z = √ r ² + (x_L - x_С)² = r.

Это равенство, очевидно, будет иметь место, если x_L = х_С , т. е. реактивное сопротивление цепи равно нулю:

x = x_L — x_С = 0.

Выразив x_L и x_С соответственно через L, С и f, получим

2π fL =		,
2π fC

откуда

f =		= f рез
2π√ LC

где f — частота напряжения, подведенного к контуру; f _рез — резонансная частота.

Таким образом, при x_L = x_С в цепи возникает резонанс напряжений, так как резонансная частота равна частоте напряжения, подведенного к цепи.

Из выражения закона Ома для последовательной цепи

I =	U	.
√ r ^2 + (xL - xС)^2

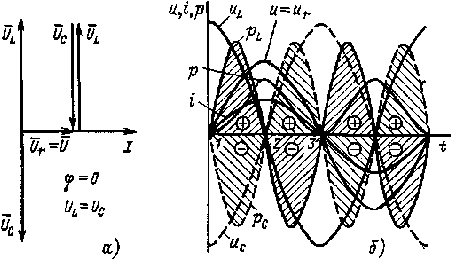
Рис. 2.14. Векторная диаграмма (а) и графики мгновенных значений и, i, р (б) цепи рис. 2.11, а при резонансе напряжений

вытекает, что ток в цепи при резонансе равен напряжению, деленному на активное сопротивление:

I = U/r.

Ток в цепи может оказаться значительно больше тока, который был бы при отсутствии резонанса. При резонансе напряжение на индуктивности равно напряжению на емкости:

Ix_L = Ix_С = U_L = U_C.

При больших значениях x_L и х_C относительно r эти напряжения могут во много раз превышать напряжение сети. Резонанс в цепи при последовательном соединении потребителей носит название резонанса напряжений.

Напряжение на активном сопротивлении при резонансе равно напряжению, приложенному к цепи:

U_r = Ir = U.

На рис. 2.14, а изображена векторная диаграмма цепи рис. 2.11, а при резонансе напряжений Диаграмма подтверждает тот факт, что ток совпадает по фазе с напряжением сети и что напряжение на активном сопротивлении равно напряжению сети. Реактивная мощность при резонансе равна нулю:

Q = Q_L - Q_C = U_LI - U_CI = 0.

так как U_L = U_C.

Полная мощность равна активной мощности;

S = √ P ² + Q ² = P,

так как реактивная мощность равна нулю. Коэффициент мощности равен единице:

cos φ = P/S = r / z = 1.

Поскольку резонанс напряжений возникает, когда индуктивное сопротивление последовательной цепи равно емкостному, а их значения определяются соответственно индуктивностью, емкостью цепи и частотой сети,

xL = 2π fL, xС =		.
2π fС

Резонанс может быть получен или путем подбора параметров цепи при заданной частоте сети, или путем подбора частоты сети при заданных параметрах цепи.

На рис. 2.14, б изображены графики мгновенных значений тока i, напряжения и сети и напряжений и_L , и_C , и_r на отдельных участках, а также активной р = iu_r и реактивной p_L= iи_L ,
p_С = iи_С мощностей за период для цепи рис. 2.11. а при резонансе напряжений. С помощью этих графиков можно проследить энергетическне процессы, происходящие в цепи при резонансе напряжений.

Активная мощность р все время положительна, она поступает из сети к активному сопротивлению и выделяется в нем в виде тепла. Мощности p_L и р_С знакопеременные, и, как видно из графика, их средние значения равны нулю.

В момент времени t = 0 (точка I на рис. 2.14, б) ток в цепи i = 0 и энергия магнитного поля
W_L = 0. Напряжение на емкости равно амплитудному значению U_тС, конденсатор заряжен и энергия его электрического поля

WC =	U ^2 тcС	.

В первую четверть периода, в интервале времени между точками 1 и 2, напряжение на емкости и, следовательно, энергия электрического поля убывают. Ток в цепи и энергия магнитного поля возрастают.

В конце первой четверти периода (точка 2) и_С = 0, W_С = 0. i = I_m, W_L = I ² _mL/ 2.

Таким образом, в первую четверть периода энергия электрического поля переходит в энергию магнитного поля.

Так как площади p_С (t) и p_L (t), выражающие запас энергии соответственно в электрическом и магнитном полях, одинаковы, вся энергия электрического поля конденсатора переходит в энергию магнитного поля индуктивности. Во вторую четверть периода, в интервале между точками 2 и 3, энергия магнитного поля переходит в энергию электрического поля.

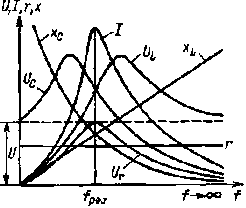
Рис. 2.15. Графики зависимости I, r, х_C, х_L, U_r, U_L, U_C от частоты цепи, изображенной на рис 2.11, а

Аналогичные процессы происходят и в последующие четверти периода.

Таким образом, при резонансе реактивная энергия циркулирует внутри контура от индуктивности к емкости и обратно. Обмена реактивной энергией между источниками и цепью не происходит. Ток в проводниках, соединяющих источник с цепью, обусловлен только активной мощностью.

Для анализа цепей иногда используют частотный метод, позволяющий выяснить зависимость параметров цепи и других величин oт частоты.

На рис 2.15 изображены графики зависимости U_r, U_C, U_L, I, х_C, х_L, от частоты при неизменном напряжении сети.

При f = 0 сопротивления x_L = 2π fL = 0,
х_C = 1 / 2π fC = ∞, ток I = 0, напряжения U_r = I_r = 0,
U_L = Ix_L= 0, U_C = U.
При f = f _pез х_L = х_C, I = U/r, U_L = U_C, U_r = U. При f → ∞ x_L →∞, х_C → 0, U_r → 0, U_C → 0, U_L → U.

В интервале частот от f = 0 до f = f _pез нагрузка имеет активно-емкостный характер, ток опережает по фазе напряжение сети. В интервале частот f = f _pез до f → ∞ нагрузка носит активно-индуктивный характер, ток отстает по фазе от напряжения сети.

Наибольшее значение напряжения на емкости получается при частоте, несколько меньшей резонансной, на индуктивности - при частоте, несколько большей резонансной.

Явления резонанса широко используются в радиоэлектронных устройствах и в заводских промышленных установках.

Пример 2.4. Определить частоту сети, при которой в цепи рис. 2.11, а возникает резонанс напряжений. Определить также, во сколько раз напряжение на индуктивности больше напряжения сети при резонансе, если цепь имеет следующие параметры:

r = 20 Ом, L = 0,1 Гн, С = 5 мкф.

Решение. Резонансная частота

f pез =		=		= 224 Гц.
2π √LC	2•3,14•√0,1•5•10^-6

Индуктивное сопротивление цепи при резонансе

x_L = 2π f _pез L - 6,28 • 224 • 0,l = 140 Ом.

Напряжение на индуктивности при резонансе

UL	=	IxL	, UL = U	xL	= U		= 7 U.
U	Ir	r

Напряжение на индуктивности при резонансе в 7 раз больше напряжения сети.

Резонанс в электрической цепи.
Резонанс в электрической цепи — явление резкого возраста­ния амплитуды вынужденных колебаний тока при приближении частоты внешнего напряжения (эдс) и собственной частоты колебательного кон­тура.
Из выражения для полного сопротивления переменному току 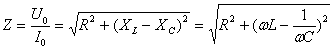видим, что сопротивление будет минимальным (сила тока при заданном напряжении – максимальной) при услови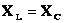и или .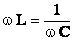
Следовательно, 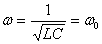- т.е. частота изменения внешнего напряжения равна собственной частоте колебаний в контуре.
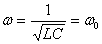
Амплитуды колебаний напряжения на индуктивности и емкости будут равны 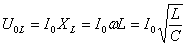и 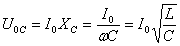- т.е. они равны по величине и противоположны по фазе (напряжение на индуктивности опережает по фазе напряжение на емкости на p).
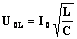
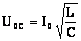
Следовательно, .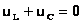
Полное падение напряжения в контуре равно падению напряжения на активном сопротивлении. Амплитуда установившихся колебаний тока будет опреде­ляться уравнением 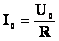. В этом и состоит смысл явления резонанса.
При этом если величина 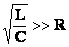, то напряжения на емкостной и индуктивной нагрузках могут оказаться много больше внешнего напряжения (эдс генератора)!
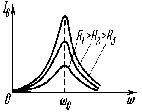
На рисунке представлена зависимость тока в колеба­тельном контуре от частоты при значениях R, гдеR1<R2<R3.
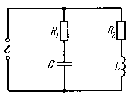
В параллельном контуре при малых активных сопротивлениях R1 и R2 токи в параллельных ветвях противоположны по фазе. Тогда, согласно правилу Кирхгофа .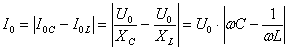
В случае резонанса 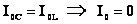. Резкое уменьшение амплитуды силы тока во внешней цепи, питающей параллельно соединенные емкостное и индуктивное сопротивления при приближении частоты внешнего напряжения к собственной частоте колебательного контура наз. резонансом токов.
Применение: одно из основных применений резонанса в электрической цепи – настройка радио и телевизионных приемников на частоту передающей станции. Необходимо учитывать резонансные явления, когда в цепи, не рассчитанной на работу в условиях резонанса, возникают чрезмерно большие токи или напряжения (расплавление проводов, пробой изоляции и т.д.).

44.45.Вихревое электрическое поле. Первое уравнение Максвелла. Применение и наблюдение вихревых полей.

Как мы знаем из закона электромагнитной индукции Фарадея, в замкнутом контуре индуцируется ЭДС при изменении магнитного потока, пронизывающего этот контур

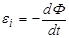. (3.93)

Если контур (проводник) движется, то причиной возникновения ЭДС может быть сила Лоренца. Если же контур неподвижен, то и в этом случае, как показывает опыт, в нём возникает ЭДС, определяемая уравнением (3.93). Какова же в этом случае причина возникновения ЭДС? Под действием ЭДС в контуре возникает электрический ток. Это значит, что на электроны проводника действует электрическое поле. Если контур жёсткий, то можно записать

,

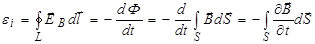или

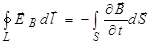. (3.94)

(Мы поставили знак частной производной, поскольку магнитная индукция может зависеть и от координаты и от времени.) Из 14.2 следует, что циркуляция этого поля по замкнутому контуру не равна нулю, в отличие от электростатического поля. Максвелл предположил, что изменяющееся во времени магнитное поле порождает вихревое электрическое поле, независимо от того, имеется у нас проводящий контур или нет. Просто если он есть, то позволяет зарегистрировать вихревое электрическое поле Е_В.

Левую часть уравнения (3.94) можно преобразовать по формуле Стокса 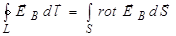. Тогда, вместо уравнения (3.94), получим

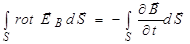. (3.95)

Поскольку интегрирование может производиться по любой поверхности, опирающейся на контур L, то в каждой точке этой поверхности должны равняться подынтегральные выражения

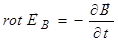. (3.96)

Поле Е_В существенно отличается от электростатического поля, для которого, как мы помним, циркуляция по замкнутому контуру равна нулю: 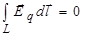, а значит, в соответствии с теоремой Стокса, и ротор этого поля в любой точке равен нулю:

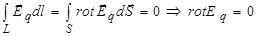. (3.97)

В общем случае

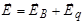, (3.98)

но для ротора суммарного поля, в силу уравнения (3.97), остаётся справедливым соотношение (3.96). Таким образом,

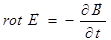. (3.99)

Поскольку переменное магнитное поле порождает электрическое, как это следует из закона индукции Фарадея и полученной нами из этого закона формулы (3.99), то должно существовать и обратное явление – переменное электрическое поле должно порождать магнитное поле. Для установления количественных соотношений рассмотрим процесс заряда конденсатора.

Рисунок 3.21

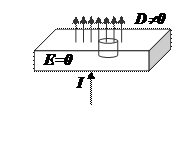
Для начала определим поле вблизи поверхности металлической обкладки конденсатора. Применим терему Гаусса для вектора электрического смещения к одной из обкладок (рис. 3.21). Внутри металла поле равно нулю, а снаружи направлено перпендикулярно поверхности. Следовательно, поток через весь цилиндр сведётся к потоку через верхнее основание цилиндра площадью dS. И этот поток должен равняться заряду, заключённому внутри нашего цилиндра, или DdS=sdS, или

D=s. (3.100)

Здесь s – поверхностная плотность зарядов на обкладке конденсатора.

Как мы уже говорили, Максвелл предположил, что изменяющееся электрическое поле создаёт магнитное поле. Но мы знаем, что постоянное магнитное поле создаётся токами. Поэтому естественно предположение, что должен быть ещё один ток, который Максвелл назвал током смещения и который ответственен за создание магнитного поля. Для установления вида этого тока смещения, рассмотрим соотношение (3.100) справа налево, а именно

s =D. (3.101)

Умножим обе части на площадь пластины S и получим

q = sS= DS. (3.102)

Здесь q – заряд пластины конденсатора. Во время заряда конденсатора ток в подводящем проводе

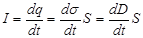. (3.103)

Разделив обе части последнего уравнения на площадь пластины S, получим слева ток проводимости j=I/S, а справа – плотность нового, максвелловского тока, или плотность тока смещения. Таким образом,

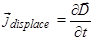. (3.104)

В последнем уравнении мы поставили значки векторов – для общего случая и написали частную производную, поскольку в общем случае вектор электрического смещения может зависеть и от координаты.

Проанализировав полученные результаты, Максвелл ввёл понятие общего тока как суммы токов проводимости и тока смещения. Здесь подчеркнём, что ток смещения – это просто название изменяющегося во времени электрического поля. Единственная функция тока смещения – создавать магнитное поле. Тогда обобщенный закон полного тока будет иметь вид

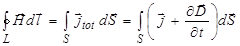, (3.105)

или окончательно

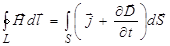. (3.106)

Максвелл создал замкнутую макроскопическую теорию электромагнитного поля. В основе этой теории лежат его знаменитые уравнения. Первая пара связывает основные характеристики электрического и магнитного полей

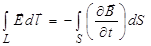; (3.107)

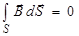. (3.108)

В уравнении (3.107) под полем E надо понимать полное поле – поле, созданное неподвижными зарядами, и поле, созданное изменяющимся магнитным полем. Уравнение (3.108) отражает тот факт, что в природе нет магнитных зарядов.

Вторая пара уравнений Максвелла связывает вспомогательные характеристики электрического и магнитного полей

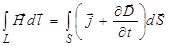; (3.109)

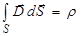. (3.110)

Уравнение (3.109) является следствием того, что магнитное поле создаётся как токами проводимости, так и токами смещения (изменяющимся во времени электрическим полем). И уравнение (3.110) говорит нам, что источниками электрического поля (помимо изменяющегося магнитного поля) являются электрические заряды. Уравнения Максвелла (3.107)…(3.110) называются уравнениями Максвелла в интегральной форме.

Уравнения Максвелла дополняются так называемыми материальными уравнениями, которые устанавливают связь между вспомогательными и основными характеристиками полей. Для однородной и изотропной неферромагнитной среды эти уравнения имеют вид

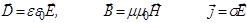(3.111)

Уравнения Максвелла не симметричны относительно электрического и магнитного полей, поскольку в природе нет магнитных зарядов.

Уравнения Максвелла позволили предсказать существование электромагнитных волн – распространяющихся в пространстве со скоростью света переменных электрического и магнитного полей. Вскоре электромагнитные волны были обнаружены немецким физиком Г.Герцем. Оказалось, что их свойства полностью описываются уравнениями Максвелла. Это также позволило Максвеллу создать электромагнитную теорию света – как электромагнитных волн с длиной волны .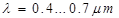

Если применить к уравнениям (3.107)…(3.110) теоремы Гаусса и Стокса, то получим уравнения Максвелла в дифференциальной форме:

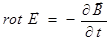; (3.112)

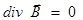; (3.113)

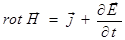; (3.114)

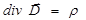. (3.115)

Уравнения (3.98)…(3.101) связывают локальные характеристики поля в каждой точке.

.

46.Система уравнений Максвелла.

Дата добавления: 2014-12-16