Справочная информация. Алгебраической задачей на собственные значения называется задача определения нетривиальных (ненулевых) решений системы линейных однородных алгебраических

ЗНАЧЕНИЯ

АЛГЕБРАИЧЕСКАЯ ЗАДАЧА НА СОБСТВЕННЫЕ

Алгебраической задачей на собственные значения называется задача определения нетривиальных (ненулевых) решений системы линейных однородных алгебраических уравнений с параметром. Простейшая из них записывается в виде

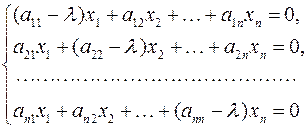
или

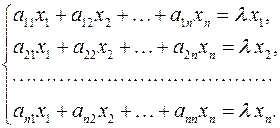
В матричной форме задача на собственные значения формулируется следующим образом

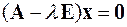или или ,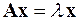

где

, , , .

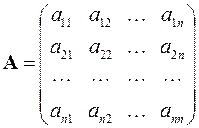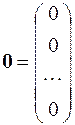Система линейных однородных алгебраических уравнений имеет бесчисленное множество нетривиальных решений, когда её определитель

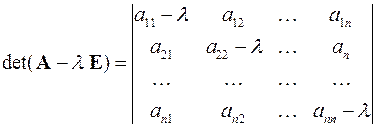
равен нулю. В противном случае она имеет единственное решение – тривиальное: .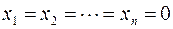

Условие существования нетривиальных решений, после «раскрытия» определителя, может трактоваться как задача поиска корней характеристического уравнения системы:

,

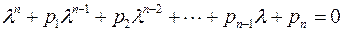где коэффициенты уравнения p ₁, p ₂,..., p_n вычисляются через элементы матрицы A.

Из алгебры многочленов известно, что алгебраическое уравнение n -го порядка с действительными коэффициентами имеет n корней, среди которых могут быть действительные корни, чётное количество комплексно-сопряжённых корней и равные (кратные) корни. Ниже будут рассмотрены случаи, когда характеристическое уравнение системы имеет только действительные и различные корни, которые для определённости упорядочены следующим образом

.

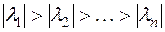К действительным корням характеристического уравнения приводят задачи с симметричными матрицами.

Каждому значению параметра – собственному значению матрицы A, соответствует своё бесчисленное множество нетривиальных решений исходной системы.

Равенство нулю определителя системы при указывает на линейную зависимость её уравнений, когда одно из её уравнений является линейной комбинацией остальных. В этом случае для определения вектора решения

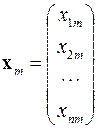
достаточно рассмотреть систему из (n – 1)-го уравнения, например:

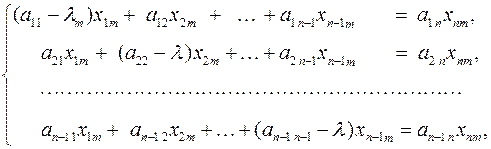
где для определенности отброшено последнее уравнение. Решение такой системы позволяет однозначно определить составляющие вектора x _m через одну из его компонент, в данном случае 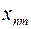. Эта компонента, являясь произвольной постоянной, может принимать бесчисленное мно­жество ненулевых значений, поэтому полученное множество решений будет соответствовать бесконечному количеству коллинеарных векторов x _m, отличающихся друг от друга только длиной. Исключение этой неопределённости достигается нормированием вектора x _m. Обычно для этого используется евклидова норма с учётом знака максимальной по модулю составляющей вектора

, т.е. ,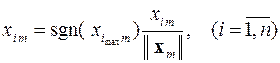

где

.

Такой подход даёт возможность однозначно определить для каждого собственного значения системы свой вектор нетривиального решения 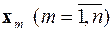, который называется собственным вектором.

Все собственные векторы x ₁, x ₂,..., x _n матрицы A являются линейно независимыми. В случае, когда матрица A симметрична, собственные векторы ещё и ортогональны – скалярное произведение любого собственного вектора на любой другой равно нулю

.

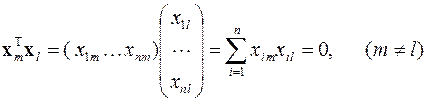Наличие у алгебраической задачи на собственные значения n решений в виде n собственных значений и n собственных векторов позволяет записать эту задачу еще в одной форме. Она основана на том, что все собственные векторы в виде столбцов, начиная с 1-го и кончая n -м, собирают в квадратную матрицу, а собственные значения расставляют в том же порядке в диагональной матрице

, .

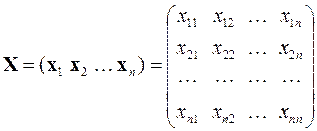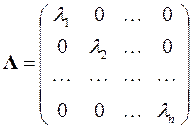В результате алгебраическая задача на собственные значения приобретает следующий вид

.

Иллюстрацией рассказанного выше может служить следующая задача определения собственных чисел и собственных векторов

.

Она состоит в отыскании нетривиальных решений системы однородных алгебраических уравнений

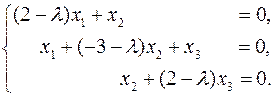
Существование нетривиальных решений у такой системы уравнений возможно при равенстве нулю её определителя

.

Его «раскрытие» по элементам первой строки даёт характеристическое уравнение

.

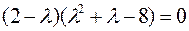Корни такого уравнения (собственные числа исходной задачи) имеют значения

.

Для отыскания собственных векторов задачи каждое собственное значение подставляется в исходную ему систему однородных алгебраических уравнений

® ® ,

® ® ,

® ® .

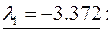
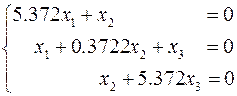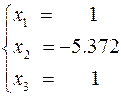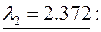
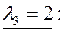
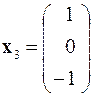Полученные векторы должны быть пронормированы. С помощью евклидовой нормы это будет выглядеть следующим образом.

, ® ,

, ® ,

, ® .

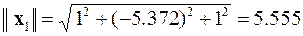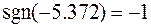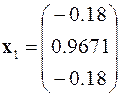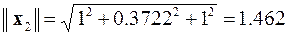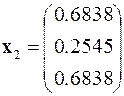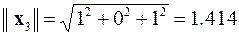Для решения задачи на собственные значения большой размерности (n > 5) используются итерационные методы, к которым относятся метод простых итераций, метод одновременных итераций, метод Якоби и другие.

Метод одновременных итераций (A.Jennings, 1967)

Данный метод позволяет находить последовательную группу собственных векторов x ₁, x ₂,..., x _m (m < n), соответствующих m наибольшим по модулю собственным значениям l ₁, l ₂,…, l_m матрицы A, а также сами эти собственные значения. Здесь рассматривается его алгоритм применительно к симметричным матрицам.

В качестве начального приближения группы собственных векторов, которые должны быть линейно независимыми, можно взять семейство ортогональных и нормированных (ортонормированных) векторов следующего вида

.

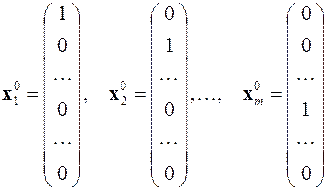Для них организуется одновременный итерационный процесс с принудительной ортогонализацией и нормированием, как правило, с использованием евклидовой нормы. В компактном виде, где собственные векторы объединены в прямоугольную матрицу X

.

итерационный процесс будет записываться следующим образом

, ,

, ,

…………………………..

, ,

…………………………..

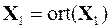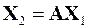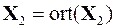Для ортонормирования семейства векторов x ₁, x ₂,..., x _m, образующих матрицу X применяется алгоритм Грама–Шмидта, который заключается в следующем. Первый вектор ортонормированного семейства векторов получается путем нормирования вектора x ₁

.

Далее вычисляется скалярное произведение вектора x ₂ и полученного вектора x ₁

,

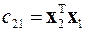с помощью которого пересчитывается второй вектор x ₂

,

являющийся после нормирования вторым нормированным вектором x ₂, ортогональным к вектору x ₁

.

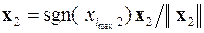Далее процесс повторяется для оставшихся векторов x ₃,..., x _m

,

,

,

,

……………………………………………………….

,

.

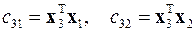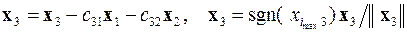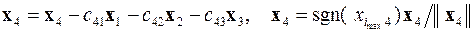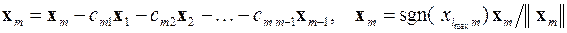В результате получаются нормированные и взаимно ортогональные векторы x ₁, x ₂,..., x _m. Эта операция над векторами выполняется на каждой итерации и итерационный процесс останавливается при выполнении условия его завершения.

По окончании итераций собственные значения, соответствующее найденным на k -ой итерации собственным векторам, определяются с помощью соотношения Рэлея

.

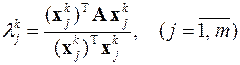Сходимость метода одновременных итераций

и оценка его погрешности

Если последовательность группы векторов 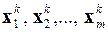(k = 0, 1, 2,...) имеет конечный предел – тоже группу векторов, то итерационный процесс метода одновременных итераций сходится. Получающаяся группа m собственных векторов соответствует m самым большим по модулю собственным векторам матрицы A.

Условия сходимости процесса итераций описывается следующим образом: если m наибольших по модулю собственных значений матрицы A не являются кратными, то при любом начальном приближении векторов 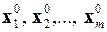последовательность группы векторов 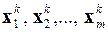(k = 0, 1, 2,...) сходится к собственным векторам . При этом скорость сходимости последовательности группы векторов 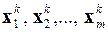различна для каждого вектора и определяется отношениями 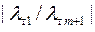, ,…, . Абсолютная погрешность вычисления каждого из получаемых векторов на k -ой итерации имеет оценку

,

,

…………………………..………..

,

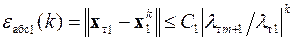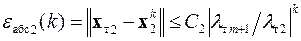где С ₁, С ₂,…, С_m – коэффициенты, определяемые свойствами матрицы A и случайностью выбора векторов 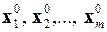начального приближения.

На практике итерации завершают при выполнении условия

,

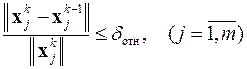где δ _отн – требуемая относительная разница между соседними приближениями собственных векторов. Её значение часто принимается на порядок меньше необходимой относительной погрешности.

Иллюстрацией алгоритма метода одновременных итераций может служить решение задачи определения двух наибольших по модулю собственных значений и соответствующих им собственных векторов матрицы

с относительной разницей между соседними приближениями собственных векторов не более, чем 10^–2.

В качестве начального приближения выбираются два ортонормированных вектора, записанных в виде прямоугольной матрицы

.

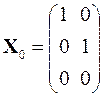Первая итерация:

,

, ,

,

,

, ,

.

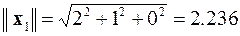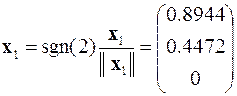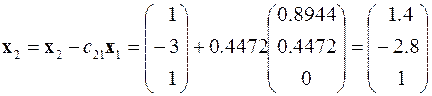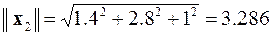Вторая итерация:

,

,

,

,

,

,

,

.

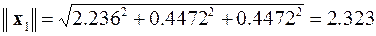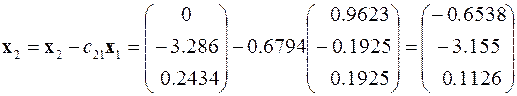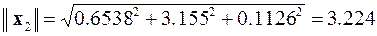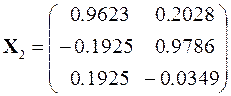Далее процесс вычислений повторяется. На 3-й итерации он даёт следующее приближение собственных векторов

,

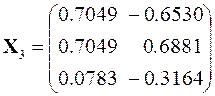и только на 21-й итерации с приближением собственных векторов

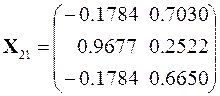
можно прекратить процесс их уточнения, поскольку относительная разница между 20-м и 21-м приближениями собственных векторов имеет величину меньшую заданной

,

,

,

.

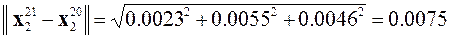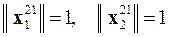В результате два наибольших по модулю собственных значения рассматриваемой матрицы будут

,

,

,

, .

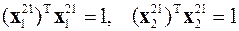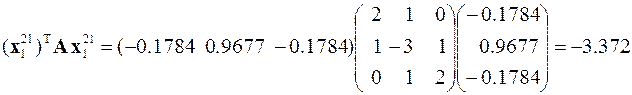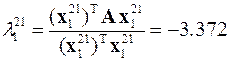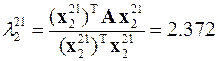О начальном приближении метода одновременных итераций

Метод одновременных итераций чувствителен к начальным приближениям итерируемых векторов. Их удачный выбор позволяет сократить число необходимых итераций в 3–4 раза. Практика показывает, что наиболее универсальным способом является выбор начальных приближений собственных векторов с помощью полиномов Чебышёва 1-го рода

,

,

,

…………………………

,

……………………

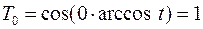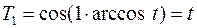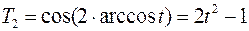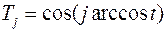Они ортогональны на отрезке 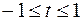, благодаря чему можно получить систему из m линейно независимых векторов, близких к ортонормированным. Их компоненты определяются формулами

.

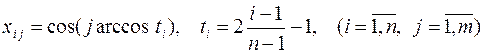Отыскание наименьших собственных значений

В случае, когда требуется найти серию из m наименьших по модулю собственных значений матрицы А и соответствующие им векторы решают задачу на собственные значения для обратной матрицы А ^–1. В такой постановке исходная задача определения собственных значений в матричной форме записывается в ви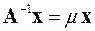де

, где .

Для неё строится следующий итерационный процесс

, ,

, ,

…………………………..

, ,

………………..…………..

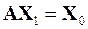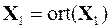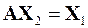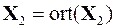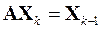По завершению итераций, например на k -ой итерации, с помощью соотношения Релея определяются в k -ом приближении m наибольших по модулю собственных значений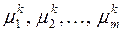

,

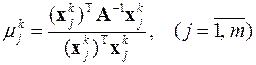которые будут соответствовать m наименьшим по модулю собственным значениям 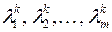исходной матрицы А

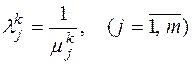
Найденные собственные векторы будут соответствовать и собственным значениям 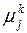, и собственным значениям .

Обобщённая задача на собственные значения

Обобщённая задача на собственные значения записывается в виде следующего матричного уравнения

,

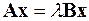где A и B – квадратные матрицы. Если вторая матрица B этого уравнения является единичной, то обобщённая задача переходит в рассмотренную выше классическую задачу на собственные значения. Присутствие в уравнении не единичной матрицы B не позволяет применять для его решения рассмотренные методы без их видоизменения.

На практике к такой задаче приводятся задачи об устойчивости и свободных колебаниях упругих конструкций. Поэтому, как правило, матрицы A и B являются симметричными и одна из них – положительно определённая. Это означает, что все её собственные значения положительны. В этом случае обобщённую задачу на собственные значения можно привести к классическому виду и применять рассмотренные методы.

Этот приём основан на свойстве положительно определённых матриц, которое заключается в том, что их можно представить в виде произведения верхней треугольной матрицы и её транспонированной матрицы. То есть матрицу B, если она – положительно определённая, можно представить в виде

.

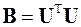Для этого ненулевые элементы матрицы U вычисляются на основе элементов матрицы B по следующим формулам:

- элементы 1-й строки

;

- элементы со 2-й строки по (n –1)-ю строку (i = 2, 3,…, n –1)

;

- последний элемент n -ой строки

.

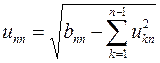Такое представление матрицы B позволяет записать уравнение обобщённой задачи на собственные значения в виде

,

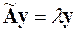где матрица и собственный вектор y записывается через матрицу A и собственный вектор x следующим образом

, .

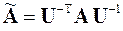Решение этого уравнения одним из методов решения задачи на собственные значения в классической постановке позволит получить его собственные значения λ ₁, λ ₂,…, λ_m (m < n) и собственные векторы y ₁, y ₂,…, y _m. Пересчёт последних с помощью обратной матрицы U

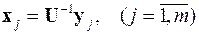
даёт возможность найти решение исходной обобщённой задачи на собственные значения.

Дата добавления: 2014-12-16