Пример решения на ПЭВМ. Программное обеспечение

Программное обеспечение

Для решения систем нелинейных алгебраических уравнений в составе библиотеки Matlab’а имеется модуль fsolve. Обращение к нему осуществляется командой

[x,f]=fsolve(fx,x0,opt,P1,P2,...);

В качестве параметров в этой функции используются:

fx	–	функция, вычисляющая вектор f(x) левых частей системы нелинейных алгебраических уравнений;
x0	–	вектор компонент начального приближения x0 к решению системы уравнений;
opt	–	структура, задающая параметры вычислительного процесса функции fsolve. Это необязательный параметр. При его отсутствии функция fsolve использует настройки по умолчанию, в частности, максимально допустимая относительная погрешность решения принимается равной 10^–6;
P1,P2,...	–	необязательные параметры, которые могут потребоваться для описания вектора f(x) левых частей системы нелинейных алгебраических уравнений.

Функция fx, вычисляющая вектор f (x) левых частей системы нелинейных алгебраических уравнений должна быть оформлена следующим образом:

function f=fx(x,P1,P2,...)

f(1)=......................;

...........................;

f(n)=......................;

end

Здесь f – массив значений вектора f (x) левых частей системы уравнений, а x – массив значений вектора решения x системы уравнений.

Структура opt содержит информацию о настройках функции fsolve. Их перечень можно получить с помощью команды optimset без параметров.

Если требуется установить параметры процесса решения нелинейных алгебраических уравнений, отличные от тех, которые используются по умолчанию, например иную относительную погрешность решения (10^–5 вместо 10^–6) и ограничение по числу итераций (не более 30), то можно воспользоваться командой

options=optimset('TolX',1.0e-5,’MaxIter’,30);

Результатом обращенияк функции fsolve являются массив x, содержащий искомые значения компонент вектора x решения системы нелинейных алгебраических уравнений и массив f со значениями компонент вектора левых частей системы при найденных компонентах вектора её решения.

Условия задачи. Найти решение системы нелинейных алгебраических уравнений

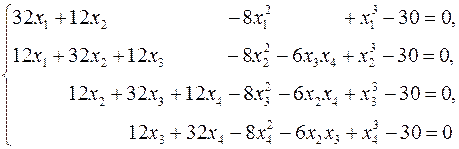
с относительной погрешностью 0.00001.

Решение. В простейшем случае, для получения одного решения системы нелинейных алгебраических уравнений достаточно воспользоваться функцией fsolve с нулевым начальным приближением.

fw=fopen('Lr_10.res','w');

x0=[0 0 0 0];

opt=optimset('TolX',1.0e-5);

[x,f]=fsolve(@fx,x0,opt);

fprintf(fw,'\n x='); fprintf(fw,'%10.6f',x);

fprintf(fw,'\n f='); fprintf(fw,'%10.6f',f);

fclose(fw);

Функция fx используется для вычисления левых частей системы нелинейных алгебраических уравнений

function f=fx(x)

f(1)=32*x(1)+12*x(2);

f(2)=12*x(1)+32*x(2)+12*x(3);

f(3)= 12*x(2)+32*x(3)+12*x(4);

f(4)= 12*x(3)+32*x(4);

f(1)=f(1)-8*x(1)^2 +x(1)^3-30;

f(2)=f(2)-8*x(2)^2-6*x(3)*x(4)+x(2)^3-30;

f(3)=f(3)-8*x(3)^2-6*x(2)*x(4)+x(3)^3-30;

f(4)=f(4)-8*x(4)^2-6*x(2)*x(3)+x(4)^3-30;

end

Результаты работы программы в виде решения заданной системы нелинейных алгебраических уравнений и значения её левых частей сохраняются в файле Lr_10.res, содержание которого показано ниже

x= 0.889007 0.597653 0.496852 1.043625

f= -0.000000 -0.000000 -0.000000 0.000000

В случае, когда, по каким-либо причинам, одно решение недостаточно для представления о рассматриваемой системе и требуется найти все её решения, то следует воспользоваться сначала методом непрерывного продолжения. С его помощью, строя траекторию решений заданной системы уравнений, можно найти начальные приближения для всех решений системы, а затем уточнить их с помощью функции fsolve так, как это было показано выше.

Основываясь на приведённом выше описании метода непрерывного продолжения, в исходную систему уравнений следует ввести параметр t

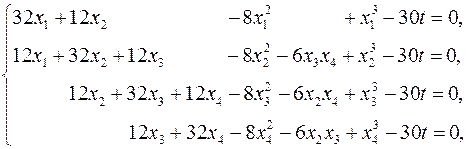
при нулевом значении которого записанная система имеет тривиальное – нулевое решение, а при t = 1 – искомое решение исходной системы.

Применение идеи равноправия аргументов системы уравнений с параметром t позволяет переписать эту систему в виде

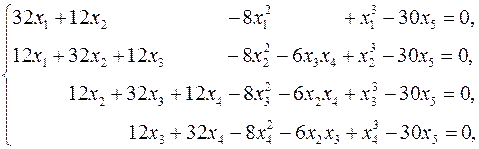
после чего можно воспользоваться наилучшим параметром продолжения – длиной траектории решений s в пространстве аргументов x ₁, x ₂, x ₃, x ₄ и x ₅

Система уравнений продолжения получается дифференцированием системы уравнений по параметру s. Это даёт систему обыкновенных дифференциальных уравнений, не разрешённых относительно производных

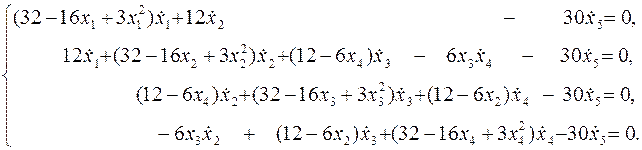
Эта система обыкновенных дифференциальных уравнений в методе непрерывного продолжения будет решаться на отрезке 0 £ s £ s _max в виде задачи Коши для нормальной системы обыкновенных дифференциальных уравнений

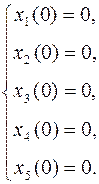
Вектор правых частей системы обыкновенных дифференциальных уравнений на каждом шаге интегрирования определяется как решение следующей системы линейных алгебраических уравнений

.

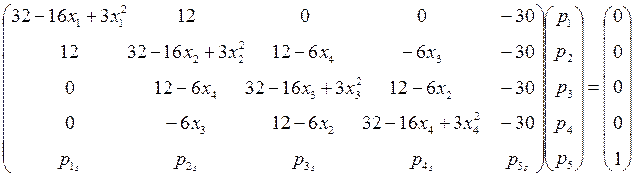с обязательным его нормированием.

Исходя из вышесказанного, программа построения траектории решений заданной системы нелинейных алгебраических уравнений будет иметь вид:

global ps;

Smax=19;

Eotn=1.0e-6;

x0=[0; 0; 0; 0; 0];

ps=[0; 0; 0; 0; 1];

opt=odeset('reltol',Eotn);

[s,x]=ode45(@fp,[0 Smax],x0,opt,Eotn);

plot(x(:,1),x(:,5),'-k',x(:,2),x(:,5),'--k',...

x(:,3),x(:,5),':k',x(:,4),x(:,5),'-.k');

grid on; xlabel('x1, x2, x3, x4'); ylabel('x5 = t');

legend('x1','x2','x3','x4');

Правые части нормальной системы дифференциальных уравнений продолжения вычисляются в функции fp

function p=fp(s,x,Eotn)

global ps;

dg=dgxt(x,ps,Eotn);

b=0;

b(5)=1;

p=dg\b';

norm=sqrt(p'*p); p=p/norm;

ps=p;

end

Расширенная и дополненная матрица Якоби рассматриваемой системы нелинейных алгебраических уравнений вычисляется с помощью центральной конечной разности в функции dgxt

function dg=dgxt(x,ps,Eotn)

for i=1:4;

xt(i)=x(i);

end;

for j=1:4;

for i=1:4; dx(i)=0; end;

if abs(xt(j))<1; h=0.1*Eotn;

else; h=0.1*Eotn*abs(xt(j));

end;

dx(j)=h;

dg(:,j)=(fx(xt+dx)-fx(xt-dx))/(2*h);

end;

dg(:,5)=-30; dg(5,:)=ps';

end

Результатом работы программы построения траектории решений будут графики зависимости компонент вектора решения системы от параметра t = x ₅, которые показаны на рис.2.

С помощью полученных графиков можно найти приближённые значения компонент решений исходной системы нелинейных алгебраических уравнений. Их местоположение показано кружочками на рис.2 при t = 1:

1-е решение: x ₁ = 0.8, x ₂ = 0.6, x ₃ = 0.5, x ₄ = 1.0;

2-е решение: x ₁ = –0.8, x ₂ = 4.7, x ₃ = 2.6, x ₄ = 4.4;

3-е решение: x ₁ = –1.7, x ₂ = 9.5, x ₃ = 8.7, x ₄ = 9.3.

Уточнение этих трёх начальных приближений с помощью приведённой ранее программы, использующей функцию fsolve, позволяет с погрешностью 0.00001 найти все три решения системы. Их компо-

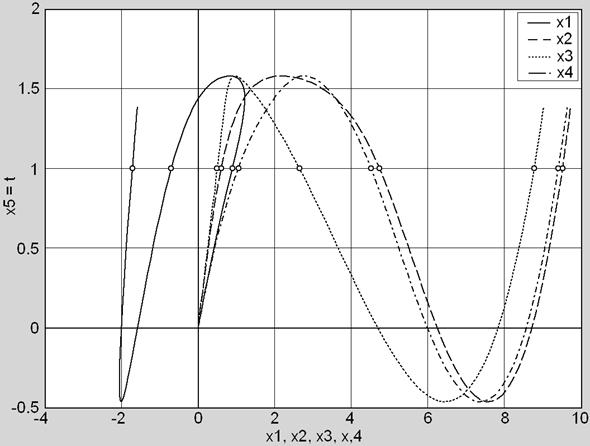
Рис.2.

ненты, сохранённые в файле Lr_10.res, имеют следующие значения

x= 0.889007 0.597653 0.496852 1.043625

f= -0.000000 -0.000000 -0.000000 0.000000

x= -0.702865 4.732590 2.643840 4.510677

f= -0.000000 -0.000000 0.000000 0.000000

x= -1.723505 9.502964 8.764113 9.400252

f= -0.000000 0.000000 0.000000 0.000000

Контрольные задания

Найти все решения (не менее 2-х) системы нелинейных алгебраических уравнений с относительной погрешностью не более чем 0.00001. Систему уравнений взять по номеру своего варианта, заменяя переменную n его номером. Верифицировать решение.

1–5.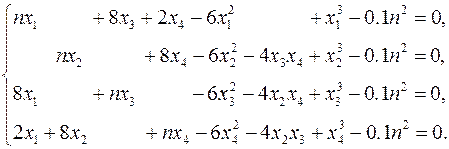

6–10.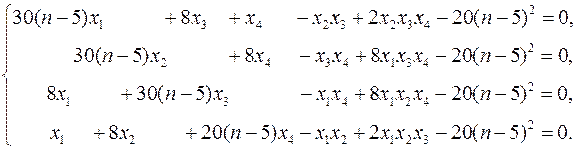
11–15.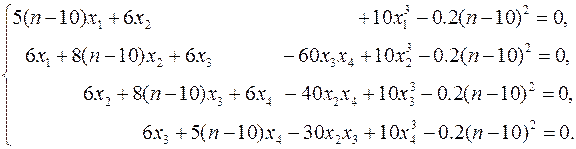
16–20.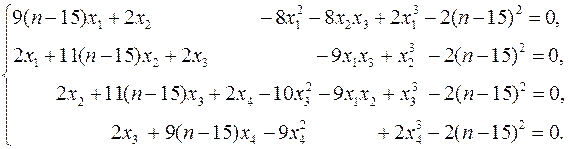
21–25.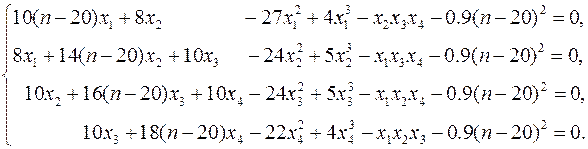
26–30.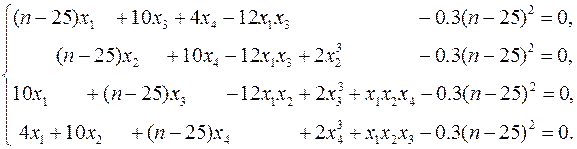

Дата добавления: 2014-12-16