Справочная информация. Оптимизация – целенаправленный процесс, заключающийся в установлении способов повышения качества реального исследуемого объекта

РЕШЕНИЕ ЭКСТРЕМАЛЬНЫХ ЗАДАЧ

Оптимизация – целенаправленный процесс, заключающийся в установлении способов повышения качества реального исследуемого объекта. К задачам этого класса можно отнести: выбор структуры и параметров технологического процесса, обеспечивающих его максимальную производительность; выбор параметров изделия, позволяющих получить его минимальную себестоимость при обеспечении требуемого уровня надежности; поиск кратчайшего маршрута перевозок по заданному списку населенных пунктов и многие другие.

Уже сами приведённые формулировки задач указывают на наличие трёх основных аспектов их постановки: критерия качества объекта, имеющего количественную оценку; управляющих параметров объекта – переменных, значения которых влияют на величину критерия качества и могут выбираться независимо, и ограничений – условий, дисциплинирующих процесс выбора значений управляющих параметров.

Решение задачи оптимизации объекта может быть осуществлено только на основе прогнозирования его поведения при изменении значений управляющих параметров. Одним из путей описания поведения объекта является построение его математической модели. Она представляет собой систему уравнений, отражающую сущность протекающих в объекте процессов и явлений. Количественная оценка критерия качества оптимизируемого объекта, являющаяся функцией его управляющих параметров называется целевой функцией. Она позволяет определить оптимальные значения управляющих параметров объекта из условия её экстремума – минимума или максимума.

Учитывая все вышесказанное, задача оптимизации объекта записывается в виде

,

где f (x) – целевая функция, x = (x ₁ x ₂... x_n)^Т – вектор управляющих параметров или переменных целевой функции, p (x) и q (x) – левые части уравнений или неравенств, выполняющих роль ограничений, налагаемых на значения управляющих параметров, p = (p ₁ p ₂... p_m)^Т, q = (q ₁ q ₂... q_k)^Т. В развёрнутой форме задача оптимизации объекта имеет вид

,

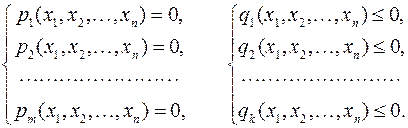
Такая задача сводится к поиску вектора параметров управления x, при котором целевая функция f (x) приводится к желаемому состоянию – минимуму или максимуму.

Таким образом, с точки зрения математики, оптимизация параметров объекта сводится к задаче поиска экстремума функции многих переменных x ₁, x ₂,..., x_n при наличии или отсутствии ограничений на их значения. Методы решения таких задач, когда сама функция и система ограничений носят нелинейный характер, называются методами нелинейного программирования. Методы этой группы относятся к поисковым методам вычислительной математики и позволяют за конечное число шагов получить решение с заданной погрешностью.

Геометрическая интерпретация задачи поиска экстремума показана на рис.1 на примере поиска минимума функции двух переменных.

Рис.1.

Для иллюстрации работы методов обычно используют проекции линий уровня на плоскость параметров, в данном случае x ₁0 x ₂. Например, на приведённом выше рисунке поиск начинается из точки M ₀, проекция которой обозначена x ₀ и имеет координаты 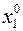и . Точка M _opt искомого минимума функции имеет проекцию x _opt.

Центральной проблемой задачи поиска экстремума функции является построение алгоритма движения, позволяющего перейти из начальной точки x ₀ в точку x _opt. Очевидно, что наиболее рациональным было бы движение в направлении обратном градиенту функции

так как направление градиента совпадает с направлением наибольшего возрастания функции.

Это не всегда возможно. Численные методы поиска экстремума в основной своей массе не вычисляют истинное значение градиента функции, а тем или иным способом осуществляют выбор общего направления поиска близкого к нему.

Другой проблемой, которую приходится решать в процессе решения задачи является управление величиной шага поиска в выбранном направлении. Находясь на большом расстоянии от точки x _opt движение рационально осуществлять с большим шагом, но в районе экстремума его величина должна быть сокращена для обеспечения требований к точности решения задачи.

Традиционно методы поиска экстремума реализуются в виде алгоритмов поиска либо минимума, либо максимума функции. Это обосновывается тем, что при необходимости задачу нахождения максимума функции всегда можно переформулировать как задачу поиска минимума и наоборот. Например, если для функции f (x) вектор x _opt соответствует точке минимума, то этот же вектор будет давать максимум функции – f (x).

Метод случайного поиска

В данном методе направление поиска экстремума выбирается путём последовательной генерации вокруг начальной точки x ₀ заданного числа случайных направлений, лучшее из которых принимается за направление градиента. При поиске минимума функции в качестве лучшего направления принимается направление на точку с наименьшим значением целевой функции, а при поиске максимума – направление на точку с самым большим её значением. Таким образом, метод не требует вычисления градиента целевой функции, а, следовательно, и её частных производных, что на практике часто невозможно. Это преимущество метода, к сожалению, влечёт за собой увеличение времени его реализации за счёт того, что поиск решения осуществляется в направлении, несколько отличающимся от направления градиента.

Это делается следующим образом. Вокруг начальной точки x ₀ строится гиперсфера радиусом ρ, на которой случайным образом выбираются m пробных точек , как показано на рис.2 для

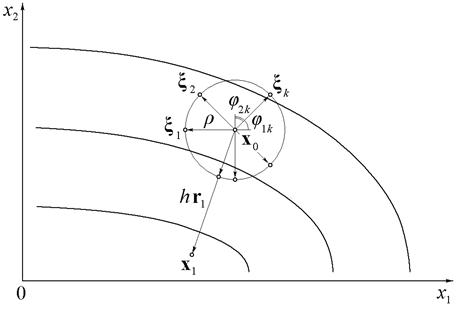
Рис.2.

случая двух управляющих параметров x ₁ и x ₂. Для каждой пробной точки формируется вектор случайных чисел, которые равномерно распределены на отрезке [–1, 1]

.

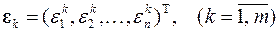Нормировка каждого такого вектора с применением квадратичной, евклидовой нормы

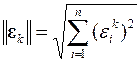
позволяет получить направляющие косинусы

.

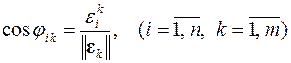для каждого вектора, соединяющего точку x ₀ и соответствующую пробную точку. Поэтому координаты пробных точек будут вычисляться по следующей зависимости:

.

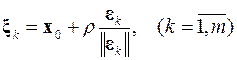В пробных точках вычисляются значения целевой функции, среди которых отыскивается минимальное. Если значение функции f (x ₀) в начальной точке удалось уменьшить в s -ой пробной точке на гиперсфере, то компоненты единичного вектора направления движения к минимуму вычисляются по формуле

,

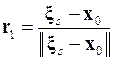где также используется евклидова норма.

Далее в этом направлении начинается спуск к минимуму функции с рабочим шагом h (см. рис.3). При этом координаты каждой новой точки в данном направлении вычисляются как

,

,

……………

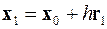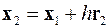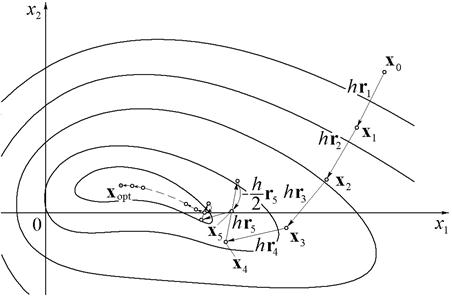
Рис.3.

Если при выполнении очередного шага значение функции выросло, то направление поиска изменяется на противоположное, а величина шага уменьшается вдвое. Такое изменение направления поиска и величины шага выполняется заданное число раз аналогично методу половинного деления. Последняя полученная точка считается лучшей в данном направлении и принимается за начальную нового цикла поиска.

Если в процессе поиска нового направления в пробных точках значения функции оказываются больше её значения в начальной точке, то процесс генерации случайных точек повторяют, уменьшив радиус ρ вдвое. Если этот процесс не приводит к отысканию лучшего направления поиска экстремума, а величина пробного радиуса ρ становится меньше наперёд заданной величины ε _абс, определяющей абсолютную погрешность метода, то поиск прекращается, а последнюю найденную точку считают экстремальной.

Учитывая случайный характер определения направления поиска, необходимо внимательно подходить к проблеме выбора количества случайных проб. Малое количество проб может существенно отклонить траекторию поиска от направления градиента, а большое – замедлить работу. Как подсказывает опыт применения данного метода, количество пробных точек обычно колеблется от 5-ти до 10-ти.

Для иллюстрации работы алгоритма метода можно воспользоваться приведённой выше задачей отыскания минимума функции

.

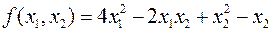В начальной точке с координатами функция имеет значение 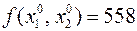. В результате выполнения первого шага поиска с 5-ю пробными точками было выполнено перемещение в точку с координатами 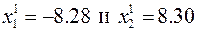, в которой целевая функция имеет значение, равное 473. Дальнейший ход решения можно отобразить следующей последовательностью координат промежуточных точек поиска

- 2-я точка ;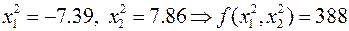

- 3-я точка ;

…………………………………………………………

- 34-я точка .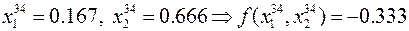

Таким образом, за 34 шага поиска был найден минимум заданной функции в точке с координатами x ₁ = 0.167 и x ₂ = 0.667. Этот результат был получен с абсолютной погрешностью 0.005.

Метод штрафных функций

Приведённый выше алгоритм не учитывает наличие ограничений на значения управляющих параметров, что существенно ограничивает его использование при решении реальных инженерных задач. Это положение может быть исправлено путем использования так называемого метода штрафных функций. Метод штрафных функций был предложен Р.Курантом (R.Courant, 1943).

Метод основан на изменении вида целевой функции, значения которой «штрафуются» – резко увеличиваются при нарушении наложенных на параметры ограничений.

В такой постановке исходная задача оптимизации объекта с ограничениями

,

преобразуется в задачу безусловной оптимизации, где целевая функция записывается в виде

.

Здесь a_i – коэффициенты штрафов, являющиеся достаточно большими положительными числами, а функции 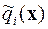имеют вид

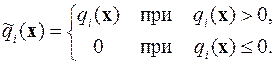
В простейшей постановке задачи можно использовать единый коэффициент штрафа, что позволяет упростить вид целевой функции

.

На рис.4 приведена иллюстрация модификации целевой функции одного параметра в случае поиска её минимума при ограничениях в виде неравенств.

Рис.4.

Таким образом, в допустимой области штрафы, определяемые функциями q_i (x), отсутствуют, а за её пределами они резко возрастают, увеличивая значение целевой функции. Это делает выход вычислительного процесса за границу допустимой области невыгодным с точки зрения минимизации целевой функции.

Коэффициент штрафа a играет очень важную роль в этом методе. С его ростом возрастает точность выполнения ограничений, но ухудшается сходимость, так как целевая функция g (x) вблизи границы приобретает характер «овражной» функции. Это обуславливается тем, что внутри «оврага» градиент функции направлен практически поперёк его ложа, делая тем самым практически невозможным движение вдоль него. Поэтому в такой ситуации придерживаются следующей последовательности действий:

- для исходной задачи строится целевая функция, учитывающая наличие ограничений;

- выбирается начальное приближение вектора x и начальное значение коэффициента штрафа a;

- решается задача оптимизации;

- если полученное решение не удовлетворяет системе ограничений, то значение коэффициента штрафа a увеличивается, и решение задачи оптимизации повторяют;

- процесс прекращается, если найденное решение удовлетворяет системе ограничений с заданной погрешностью.

Дата добавления: 2014-12-16