Проверка статистических гипотез

Статистическая гипотеза — это предположение

о виде закона распределения («данная генеральная совокупность нормально распределена»);

о значениях его параметров («генеральное среднее равно нулю»);

об однородности данных («эти две выборки извлечены из одной генеральной совокупности»).

Статистическая проверка гипотезы состоит в выяснении того, согласуются ли результаты наблюдений (выборочные данные) с нашим предположением.

Результатом проверки может быть отрицательный ответ: выборочные данные противоречат высказанной гипотезе, поэтому от нее следует отказаться. В случае ответа неотрицательного (выборочные данные не противоречат гипотезе) гипотезу принимают в качестве одного из допустимых решений (не единственно верного).

Различают основную (нулевую) гипотезу (гипотеза, которая проверяется, 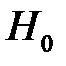) и альтернативную (конкурирующую, противопоставленную основной, 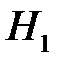). Например, если нулевая гипотеза 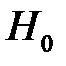: МХ = 10 (т. е. математическое ожидание нормально распределенной величины равно 10), тогда гипотеза 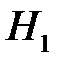, может иметь вид 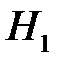: МХ ≠10.

Цель статистической проверки гипотез: на основании выборочных данных принять решение о справедливости основной гипотезы или отклонить в ее пользу альтернативной.

Так как проверка осуществляется на основании выборки, а не всей генеральной совокупности, то существует вероятность, возможно, очень малая, ошибочного заключения.

Так, нулевая гипотеза может быть отвергнута, в то время как в действительности в генеральной совокупности она является справедливой. Такую ошибку называют ошибкой первого рода, а её вероятность — уровнем значимости и обозначают a (стандартные значения a: 0.1, 0.05, 0.01, 0.001). Возможно, что нулевая гипотеза принимается, в то время как в генеральной совокупности справедлива альтернативная гипотеза. Такую ошибку называют ошибкой второго рода, а её вероятность обозначают 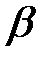Проверка статистических гипотез осуществляется с помощью статистического критерия K — правила (функции от результатов наблюдений), определяющего меру расхождения результатов наблюдений с нулевой гипотезой. Вероятность 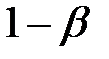называют мощностью критерия.

Замечание. Ошибка первого рода состоит в том, что будет отвергнута правильная гипотеза. Ошибка второго рода состоит в том, что будет принята неправильная гипотеза.

Например, основная гипотеза состоит в том, что предприятие получает прибыль. Если это правильная гипотеза, то ошибка первого рода состоит в том, что данная гипотеза отвергается. Если принимается решение о том, что прибыль предприятие не получает, то это ошибка второго рода.

Иногда ошибку первого рода называют «альфа-риск» (a-риск) а ошибку второго рода «бета-риск» (b-риск).

Из двух критериев, характеризующихся одной и той же вероятностью 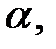выбирают тот, которому соответствует меньшая ошибка 2-го рода, т.е. большая мощность. Уменьшить вероятности обеих ошибо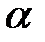к и одновременно можно, увеличив объем выборки.

Значения критерия K разделяются на две части: область допустимых значений (область принятия гипотезы 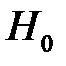) и критическую область (область принятия гипотезы 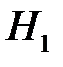). Критическая область состоит из тех же значений критерия К, которые маловероятны при справедливости гипотезы 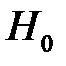. Если значение 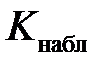критерия K, рассчитанное по выборочным данным, попадает в критическую область, то гипотеза 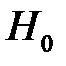отвергается в пользу альтернативной 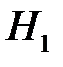в противном случае мы утверждаем, что нет оснований отклонять гипотезу .

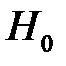Пример 4.7. Для подготовки к зачету преподаватель сформулировал 100 вопросов (генеральная совокупность) и считает, что студенту можно поставить «зачтено», если тот знает 60 % вопросов (критерий). Преподаватель задает студенту 5 вопросов (выборка из генеральной совокупности) и ставит «зачтено», если правильных ответов не меньше трех. Гипотеза 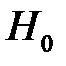: «студент курс усвоил», а множество 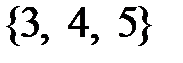— область принятия этой гипотезы. Критической областью является множество — правильных ответов меньше трех, в этом случае основная гипотеза отвергается в пользу альтернативной 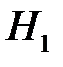«студент курс не усвоил, знает меньше 60 % вопросов».

Студент А выучил 70 вопросов из 100, но ответил правильно только на два из пяти, предложенных преподавателем, — зачет не сдан. В этом случае преподаватель совершает ошибку первого рода.

Студент Б выучил 50 вопросов из 100, но ему повезло, и он ответил правильно на 3 вопроса — зачет сдан, но совершена ошибка второго рода.

Преподаватель может уменьшить вероятность этих ошибок, увеличив количество задаваемых на зачете вопросов.

Алгоритм проверки статистических гипотез сводится к следующему:

1) сформулировать основную 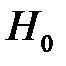и альтернативную 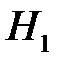гипотезы;

2) выбрать уровень значимости ;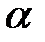

3) в соответствии с видом гипотезы 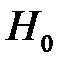выбрать статистический критерий для ее проверки, т.е. случайную величину K, распределение которой известно;

4) по таблицам распределения случайной величины K найти границу критической области 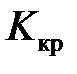(вид критической области определить по виду альтернативной гипотезы );

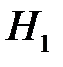5) по выборочным данным вычислить наблюдаемое значение критерия

6) принять статистическое решение: если 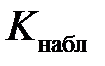попадает в критическую область — отклонить гипотезу 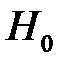в пользу альтернативной ; если 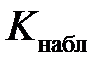попадает в область допустимых значений, то нет оснований отклонять основную гипотезу.

4.3.1 П роверка гипотез о виде распределения. критерий согласия Пирсона

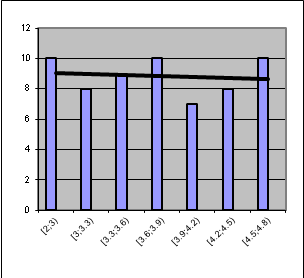
Одной из важных задач математической статистики является установление теоретического закона распределения случайной величины, характеризующей изучаемый признак по эмпирическому распределению, представляющему вариационный ряд. Предположение о виде закона распределения можно сделать по гистограмме или полигону (Рис. 4.3)

а)	б)	в)

Рис. 4.3. Возможные виды гистограмм:
а) нормального, б) показательного, в) равномерного распределений

Например, по гистограмме (рис. 4.3, а)) можно сделать предположение о том, что генеральная совокупность распределена по нормальному закону.

Для проверки гипотез о виде распределения служат специальные критерии — критерии согласия. Они отвечают на вопрос: согласуются ли результаты экспериментов с предположением о том, что генеральная совокупность имеет заданное распределение.

Проверим это предположение с помощью критерия согласия Пирсона. В этом критерии мерой расхождения между гипотетическим (предполагаемым) и эмпирическим распределением служит статистика

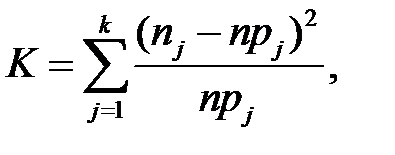
где n — объем выборки;

k — количество интервалов (групп наблюдений);

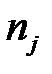— количество наблюдений, попавших в j -й интервал;

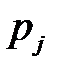— вероятность попадания в j -й интервал случайной величины, распределенной по гипотетическому закону.

Если предположение о виде закона распределения справедливо, то статистика Пирсона распределена по закону «хи-квадрат» с числом степеней свободы 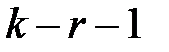(r — число параметров распределения, оцениваемых по выборке):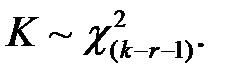

Оцениваются неизвестные параметры с использованием теории точечных оценок (см. источник [3], гл.16 и раздел 3.8. настоящего пособия), некоторые оценки приведены в табл. 4.4.

Таблица 4.4. Оцениваемые параметры и их точечные оценки

Вид распределения	Оцениваемые параметры	Точечные оценки параметров

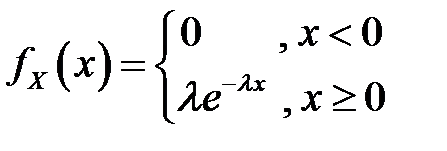
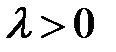
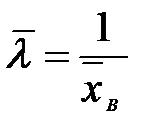
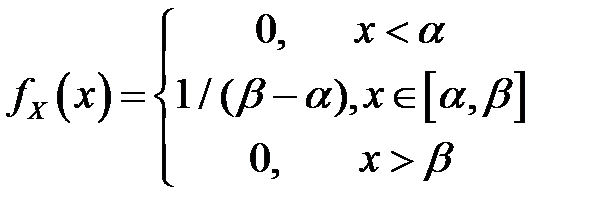
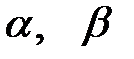
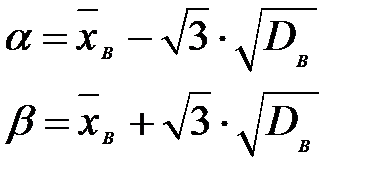
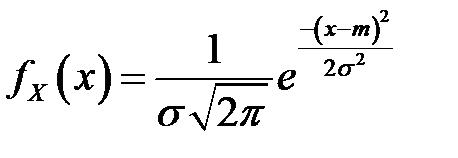
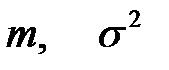
Здесь .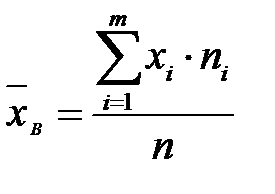

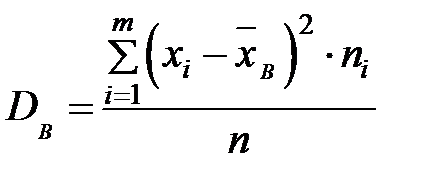Количество интервалов k рекомендуется рассчитывать по формуле Старджеса 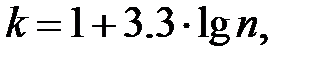где n — объем выборки. Длину i -го интервала принимают равной где 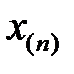—наибольшее, а 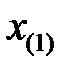— наименьшее значение в вариационном ряду.

Пример 4.8. Длясреднего балла среди 30-ти групп (с точностью до сотых долей балла) получили выборку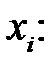

3.7, 3.85, 3.7, 3.78, 3.6, 4.45, 4.2, 3.87, 3.33, 3.76, 3.75, 4.03, 3.8, 4.75, 3.25, 4.1, 3.55, 3.35, 3.38, 3.05, 3.56, 4.05, 3.24, 4.08, 3.58, 3.98, 3.4, 3.8, 3.06, 4.38. Проверить гипотезу о нормальном распределении среднего балла на уровне значимости .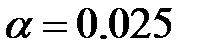

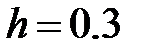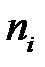Решение. Сгруппируем эту выборку. Наименьший средний балл равен 3.05, наибольший — 4.75. Интервал [3; 4.8] разобьем на 6 частей длиной , применяя формулу Старджеса (). Подсчитаем частоту (относительную частоту 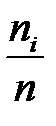) для каждого интервала и получим сгруппированный статистический ряд (табл. 4.5).

Таблица 4.5. Статистический ряд

Интервалы	[3;3.3)	[3.3;3.6)	[3.6;3.9)	[3.9;4.2)	[4.2;4.5)	[4.5;4.8)
Частоты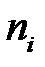
Относительные частоты	0.133	0.233	0.3	0.167	0.1	0.033

Сформулируем основную и альтернативную гипотезы.

— случайная величина X (средний балл) подчиняется нормальному закону с параметрами 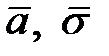. Так как истинных значений параметров 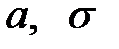мы не знаем, возьмем их оценки, рассчитанные по выборке: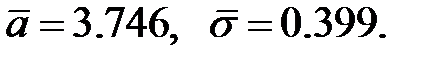

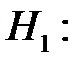случайная величина X не подчиняется нормальному закону с данными параметрами.

Рассчитаем наблюдаемое значение 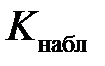статистики Пирсона. Эмпирические частоты 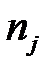уже известны (табл. 4.5), а для вычисления вероятностей 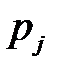(в предположении, что гипотеза 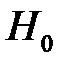справедлива) применим уже известную формулу (свойство В):

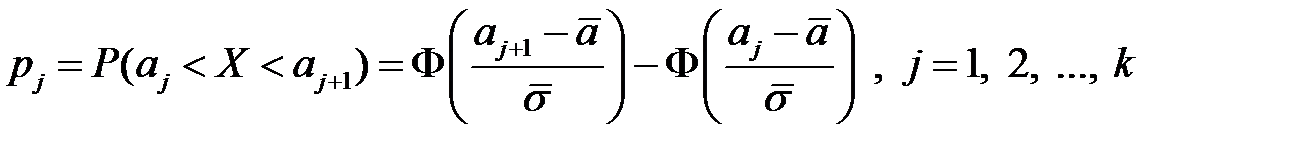
и таблицу функции Лапласа (приложение 1). Полученные результаты сведем в таблицу (табл. 4.6). Наблюдаемое значение статистики Пирсона равно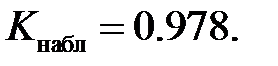

Определим границу критической области. Так как статистика Пирсона измеряет разницу между эмпирическим и теоретическим распределениями, то чем больше ее наблюдаемое значение , тем сильнее довод против основной гипотезы. 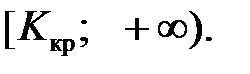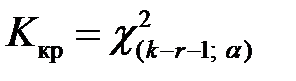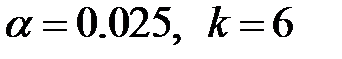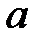Поэтому критическая область для этой статистики всегда правосторонняя: Её границу находим по таблицам распределения «хи-квадрат» (приложение 3) и заданным значениям (число интервалов), (параметры и 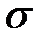оценены по выборке):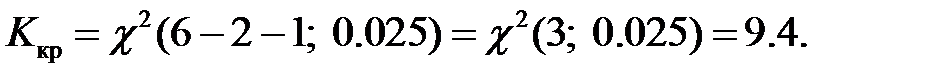

Наблюдаемое значение статистики Пирсона не попадает в критическую область: 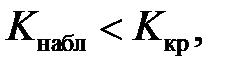поэтому нет оснований отвергать основную гипотезу.

Вывод: на уровне значимости 0.025 справедливо предположение о том, что средний балл имеет нормальное распределение.

Таблица 4.6. Сравнение наблюдаемых и ожидаемых частот

№ п/п	Интервалы группировки	Наблюдаемая частота	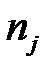Вероятность 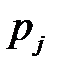попадания в j -й интервал	Ожидаемая частота	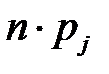Слагаемые статистики Пирсона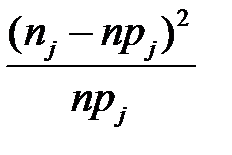
1.	[3; 3.3)		0.101	3.032	0.309
2.	[3.3; 3.6)		0.225	6.761	0.008
3.	[3.6; 3.9)		0.295	8.79	0.166
4.	[3.9; 4.2)		0.222	6.665	0.416
5.	[4.2; 4.5)		0.098	2.946	0.001
6.	[4.5; 4.8)		0.025	0.758	0.077
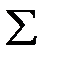
	—		0.965	28.95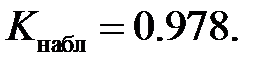

Дата добавления: 2014-12-16