Решение задач на ускорения

.

.

При этом вектор направлен перпендикулярно АМ в сторону вращения, если оно ускоренное, и против вращения, если оно замедленное; вектор 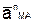всегда направлен от точки М к полюсу А (рис.24). Численно же

.

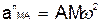Если полюс А движется не прямолинейно, то его ускорение мо­жно тоже представить как сумму касательной 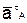и нормальной составляющих, тогда

Наконец, когда точка М движется криволинейно и ее траекто­рия известна, то можно заменить суммой .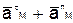

Рис.23 Рис.24

Ускорение любой точки плоской фигуры в данный момент времени можно найти, если известны: 1) векторы скорости и ускорения какой-нибудь точки А этой фигуры в данный момент; 2) траектория какой-нибудь другой точки В фи­гуры. В ряде случаев вместо траектории второй точки фигуры до­статочно знать положение мгновенного центра скоростей.

Тело (или механизм) при решении задач надо изображать в том положении, для которого требуется определить ускорение соответ­ствующей точки. Расчет начинается с определения по данным задачи скорости и ускорения точки, принимаемой за полюс.

План решения (если заданы скорость и ускорение одной точки плоской фигуры и направления скорости и ускорения другой точки фигуры):

1. Находим мгновенный центр скоростей, восставляя перпендикуляры к скоростям двух точек плоской фигуры.

2. Определяем мгновенную угловую скорость фигуры.

3. Определяем центростремительное ускорение точки вокруг полюса., приравнивая нулю сумму проекций всех слагаемых ускорений на ось, перпендикулярную к известному направлению ускорения.

4. Находим модуль вращательного ускорения, приравнивая нулю сумму проекций всех слагаемых ускорений на ось, перпендикулярную к известному направлению ускорения.

5. Определяем мгновенное угловое ускорение плоской фигуры по найденному вращательному ускорению.

6. Находим ускорение точки плоской фигуры при помощи формулы распределения ускорений.

При решении задач можно применять «теорему о проекциях векторов ускорений

двух точек абсолютно твердого тела»:

«Проекции векторов ускорений двух точек абсолютно твердого тела, которое совершает плоскопараллельное движение, на прямую, повернутую относительно прямой, проходящей через эти две точки, в плоскости движения этого тела на угол

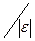
в сторону углового ускорения, равны».

Эту теорему удобно применять, если известны ускорения только двух точек абсолютно твердого тела как по модулю, так и по направлению, известны только направления векторов ускорений других точек этого тела (геометрические размеры тела не известны), не известны и ε – соответственно проекции векторов угловой скорости и углового ускорения этого тела на ось, перпендикулярную плоскости движения, не известны скорости точек этого тела.

Известны еще 3 способа определения ускорений точек плоской фигуры:

1. Способ основан на дифференцировании дважды по времени законов плоскопараллельного движения абсолютно твердого тела.

2. Способ основан на использовании мгновенного центра ускорений абсолютно твердого тела (о мгновенном центре ускорений абсолютно твердого тела будет рассказано ниже).

3. Способ основан на использовании плана ускорений абсолютно твердого тела.

МГНОВЕННЫЙ ЦЕНТР УСКОРЕНИЙ

При непоступательном движении плоской фигуры у нее в каждый момент времени имеется точка Q, ускорение которой равно нулю. Эта точка называется мгновенным центром ускорений. Определяется положение центра Q, если известны ускорение какой-нибудь точки А фигуры и величины и , следующим путем:

1) находим значение угла 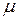, из формулы ;

2) от точки А под углом 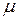, к вектору проводим прямую АЕ (рис.25);

при этом прямая АЕ должна быть отклонена от в сторону вращения фигуры, если вращение является ускоренным, и против вращения, если оно является замедленным, т. е. в сторону направления углового ускорения ;

3) откладываем вдоль линии АЕ отрезок AQ, равный

.

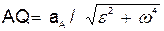Рис.25

Построенная таким путем точка Q и будет мгно­венным центром ускорений. В самом деле, известно что

,

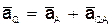где численно . Подставляя сюда значение AQ находим, что 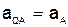. Кроме того, вектор должен образовывать с ли­нией AQ угол 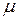, следовательно, вектор параллелен , но направлен в про­тивоположную сторону. Поэтому и .

Если точку Q выбрать за полюс, то так как 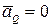, ускорение любой точки М тела, будет

.

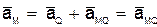При этом численно

.

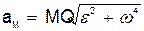Следовательно, ускорения точек плоской фигуры определяются в данный мо­мент времени так, как если бы движение фигуры, было вращением вокруг мгновенного центра ускорений Q. При этом

,

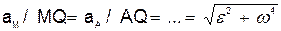т. е. ускорения точек плоской фигуры пропорциональны их расстояниям от мгно­венного центра ускорений. Картина распределения ускорений точек плоской фигуры в данный момент времени показана на рис.26.

Следует иметь в виду, что положения мгновенного центра скоростей Р и мгно­венного центра ускорений Q в данный момент времени не совпадают. Например, если колесо катится по прямолинейному рельсу (см. рис.27), причем скорость его центра С постоянна (u_С=const), то мгновенный центр скоростей находится в точ­ке Р (v_Р=0), но при этом, как было показано ; следовательно, точка Р не является одновременно мгновенным центром ускорений.

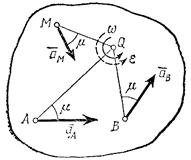
Рис.26 Рис.27

Мгновенный центр ускорений в этом случае находится, очевидно, в точке С, так как она дви­жется равномерно и прямолинейно и а_С=0. Центры скоростей и ускорений сов­падают тогда, когда фигура (тело) вращается вокруг неподвижной оси.

Понятием о мгновенном центре ускорений удобно пользоваться при решении некоторых задач.

ЛЕКЦИЯ 8

СЛОЖНОЕ ДВИЖЕНИЕ ТОЧКИ

ОТНОСИТЕЛЬНОЕ, ПЕРЕНОСНОЕ И АБСОЛЮТНОЕ ДВИЖЕНИЯ

До сих пор мы изучали движение точки или тела по отношению к одной заданной системе отсчета. Однако в ряде случаев при реше­нии задач механики оказывается целесообразным (а иногда и не­обходимым) рассматривать движение точки (или тела) одновременно по отношению к двум системам отсчета, из которых одна считается основной или условно неподвиж­ной, а другая определенным образом движется по отношению к первой. Движение, совершаемое при этом точкой (или телом), называют со­ставным или сложным. Например, шар, катящийся по палубе движу­щегося парохода, можно считать совершающим по отношению к бе­регу сложное движение, состоящее из качения по отношению к палубе (подвижная система отсчета), и движение вместе с палубой парохода по отношению к берегу (не­подвижная система отсчета). Таким путем сложное движение шара разлагается на два более простых и более легко исследуемых.

Рис.28

Рассмотрим точку М, движущуюся по отношению к подвижно системе отсчета Oxyz, которая в свою очередь как-то движется отно­сительно другой системы отсчета 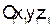, которую называем основ­ной или условно неподвижной (рис. 28). Каждая из этих систем отсчета связана, конечно, с определенным телом, на чертеже не по­казанным. Введем следующие определения.

1. Движение, совершаемое точкой М по отношению к подвиж­ной системе отсчета (к осям Oxyz), называется относительным движением (такое движение будет видеть наблюдатель, связанный с этими осями и перемещающийся вместе с ними). Траектория АВ, описываемая точкой в относительном движении, называется относи­тельной траекторией. Скорость точки М по отношению к осям Oxyz называется относительной скоростью (обозначается 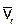), a ускорение - относительным ускорением (обозначается ). 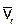Из определения следует, что при вычислении и можно движение осей Oxyz во внимание не принимать (рассматривать их как непод­вижные).

2. Движение, совершаемое подвижной системой отсчета Oxyz (и всеми неизменно связанными с нею точками пространства) по отно­шению к неподвижной системе 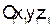, является для точки М пере­носным движением.

Скорость той неизменно связанной с подвижными осями Oxyz точки m, с которой в данный момент времени совпадает движущаяся точка М, называется переносной скоростью точки М в этот момент (обозначается 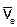), а ускорение этой точки т - переносным ускорением точки М (обозначается ). Таким образом,

.

Если представить себе, что относительное движение точки про­исходит по поверхности (или внутри) твердого тела, с которым жестко связаны подвижные оси Oxyz, то переносной скоростью (или ускорением) точки М в данный момент времени будет скорость (или ускорение) той точки т тела, с которой в этот момент совпадает точка М.

3. Движение, совершаемое точкой по отношению к неподвижной системе отсчета 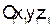, называется абсолютным или сложным. Траектория CD этого движения называется абсолютной траекто­рией, скорость - абсолютной скоростью (обозначается 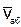) и ускорение - абсолютным ускорением (обозначается ).

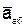В приведенном выше примере движение шара относительно палу­бы парохода будет относительным, а скорость - относительной ско­ростью шара; движение парохода по отношению к берегу будет для шара переносным движением, а скорость той точки палубы, которой в данный момент времени касается шар будет в этот момент его пере­носной скоростью; наконец, движение шара по отношению к берегу будет его абсолютным движением, а скорость - абсолютной ско­ростью шара

TEOPEMA СЛОЖЕНИЯ СКОРОСТЕЙ

Пусть некоторая точка М со­вершает движение по отношению к системе отсчета Oxyz, которая са­ма движется произвольным образом по отношению к неподвижной систе­ме отсчета 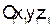, (рис.29). Поло­жение подвижной системы отсчета может быть определено, если задать положение точки О радиусом-вектором r₀, проведенным из начала неподвижной системы отсчета, и направления единичных векторов 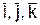подвижных осей О_X, O_Y, O_Z.

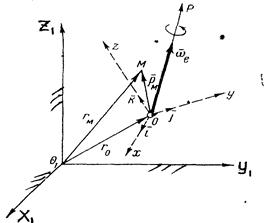
Рис.29

Произвольное переносное движение подвижной системы отсчета слагается из поступательного движения со скоростью v₀ точки О и движения вокруг мгновенной оси вращения ОР, походящей через точку О, с мгновенной угловой скоростью . Вследствие переносного движения подвижной системы отсчета радиус-вектора ₀ и направления единичных векторов 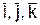изменяются. Если векторы ₀, 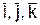заданы в функции времени, то переносное движение подвижной системы отсчета вполне определено.

Положение точки М по отношению к подвижной системе отсчета можно определить радиусом-вектором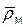

,

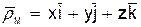где координаты x,y,z точки М изменяются с течением времени вследствие движения точки М относительно подвижной системы отсчета. Если радиус-вектор 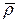_М задан в функции времени, то относительное движение точки М, т.е. движение этой точки относительно подвижной системы отсчета, задано.

Положение точки М относительно неподвижной системы отсчета 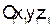, может быть определено радиусом-вектором r_M. Из рис.30 видно, что

. (1)

Если относительные координаты x,y,z точки М и векторы 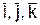определены в функции времени, то слагающееся из относительного и переносного движений составное движение точки М, т.е. движение этой точки по отношению к неподвижной системе отсчета, также надо считать заданным.

Скорость составного движения точки М, или абсолютная скорость этой точки, равна, очевидно, производной от радиуса-вектора r_M точки м по времени t

.

Поэтому, дифференцируя равенство (1) по времени t, получим

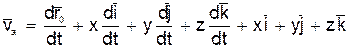. (2) 27

Разобьем слагаемые в правой части этого равенства на две группы по следующему признаку.

К первой группе отнесем те слагаемые, которые содержат производные только от относительных координат x,y и z, а ко второй - те слагаемые, которые содержат производные от векторов ₀, 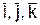, т.е. от величин, изменяющихся только вследствие переносного движения подвижной системы отсчета

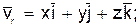(3)

. (4)

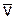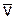Каждая из групп слагаемых, обозначенных через v_r и v_e, представляет собой, по крайней мере, по размерности некоторую скорость. Выясним физический смысл скоростей _r и _e.

Скорость , как это следует из равенства (3), вычисляется в предположении, что изменяются только относительные координаты x,y,z точки М, но векторы ₀, 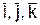остаются постоянными, т.е. подвижная система отсчета Oxyz как бы условно считается неподвижной. Итак скорость 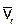представляет собой относительную скорость точки М.

Скорость 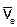вычисляется так, как будто бы точка М не двигалась относительно подвижной системы отсчета, так как производные x,y,z в равенство (4) не входят. Поэтому скорость 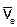представляет собой переносную скорость точки М.

Итак, 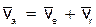. (5)

Это равенство выражает теорему сложения скоростей в случае, когда переносное движение является произвольным: абсолютная скорость точки М равна геометрической сумме переносной и относительной скоростей этой точки.

Теорема сложения ускорений

Ускорение составного движения точки М, или абсолютное ускорение этой точки, равно, очевидно, производной от абсолютной скорости точки М по времени t

Поэтому, дифференцируя равенство по времени, получим

.

Разделим слагаемые правой части этого равенства на три группы.

К первой группе отнесем слагаемые, содержащие только производные от относительных координат x,y и z, но не содержащие производные от векторов ₀, :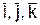

.

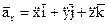Ко второй группе отнесем слагаемые, которые содержат только производные от векторов ₀, 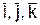, но не содержащие производных от относительных координат x,y,z:

.

Осталась еще одна группа слагаемых, которые не могли быть отнесены ни к первой, ни ко второй, так как они содержат производные от всех переменных x,y,z, 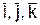. Обозначим эту группу слагаемых через :

.

Каждая из выделенных групп представляет собой, по крайней мере по размерности, некоторое ускорение. Выясним физический смысл всех трех ускорений: .

Ускорение , как это видно из равенства, вычисляется так, как если бы относительные координаты x,y,z изменялись с течением времени, а векторы ₀, 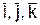оставались неизменными, т.е. подвижная система отсчета Oxyz как бы покоилась, а точка М двигалась. Поэтому ускорение представляет собой относительное ускорение точки М. Так как ускорение (и скорость) относительного движения вычисляется в предположении, что подвижная система отсчета находится а покое, то для определения относительного ускорения (и скорости) можно пользоваться всеми правилами, изложенными ранее в кинематике точки.

Ускорение , как это видно из равенства, вычисляется в предположении, что сама точка М покоится по отношению к подвижной системе отсчета Oxyz (x=const, y=const, z=const) и перемещается вместе с этой системой отсчета по отношению к неподвижной системе отсчета 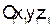. Поэтому ускорение представляет собой переносное ускорение точки М.

Третья группа слагаемых определяет ускорение 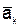, которое не может быть отнесено не к относительному ускорению , так как содержит в своем выражении производные не к переносному ускорению , так как содержит в своем выражении производные

Преобразуем правую часть равенства, припомнив, что

Подставляя эти значения производных в равенства, получим

или .

Здесь вектор 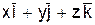есть относительная скорость точки М, поэтому

.

Ускорение 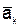называют ускорением Кориолиса. Ввиду того, что ускорение Кориолиса появляется в случае вращения подвижной системы отсчета, его называют еще поворотным ускорением.

С физической точки зрения появление поворотного ускорения точки объясняется взаимным влиянием переносного и относительного движений.

Итак, ускорение Кориолиса точки равно по модулю и направлению удвоенному векторному произведению угловой скорости переносного движения на относительную скорость точки.

Равенство, которое теперь можно сокращенно записать в виде

.

представляет теорему сложения ускорений в случае, когда переносное движение является произвольным: абсолютное ускорение точки равно векторной сумме переносного, относительного и поворотного ускоре­ний. Эту теорему часто называют теоремой Кориолиса.

Из формулы следует, что модуль поворотного ускорения будет

где а - угол между вектором 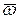_e и вектором 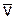_r. Чтобы определить направление поворотного ускорения 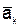, нужно мысленно перенести вектор в точку М и руководствоваться правилом векторной алгебры. Согласно этому правилу, вектор 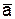нужно направлять перпендикуляр­но к плоскости, определяемой векторами и 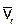, и так, чтобы, смотря с конца вектора 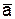, наблюдатель мог видеть кратчайший поворот от к происходящим против движения часовой стрелки (рис. 30).

Для определения направления 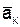можно также пользоваться следующим правилом Н. Е. Жу­ковского: чтобы получить направление поворот­ного ускорения 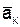, достаточно составляющую относительной скорости точки М, перпенди­кулярную к вектору , повернуть (в плоскости, перпендикулярной к вектору ) на прямой угол вокруг точки М в направлении переносного вра­щения (рис.30).

Рис.30

Если переносное движение подвижной систе­мы отсчета есть поступательное движение, то =0 и поэтому поворотное ускорение а точки также равно нулю. Поворотное ускорение равно, очевидно, нулю и в том случае, когда в данный момент времени обращается в нуль.

Кроме того, поворотное ускорение точки может, очевидно, обращать­ся в нуль, если:

а) вектор относительной скорости точки параллелен вектору уг­ловой скорости переносного вращения, т.е. относительное движение точки происходит по направлению, параллельному оси переносного вращения;

б) точка не имеет движения относительно подвижной системы от­счета или относительная скорость точки в данный момент времени равна нулю ( =о).

Дата добавления: 2014-12-17