Представление нечетких знаний

Вопросы, подлежащие изучению

6.1. Нечеткие знания и нечеткая логика.

6.2. Нечеткие множества. Нечеткие отношения.

6.3. Нечеткие выводы.

Пояснения к вопросам

6.1. Знания не всегда могут быть описаны точно – часто встречаются так называемые «нечеткие» знания.

Все нечеткости можно классифицировать следующим образом:

1) недетерминированность выводов,

2) многозначность,

3) ненадежность,

4) неполнота,

5) нечеткость или неточность.

Нечеткая логика – разновидность непрерывной логики, в которой логические формулы могут принимать истинностные значения между 1 и 0. Слабым моментом в применении нечеткой логики является функция принадлежности. Предположим, возраст Х - 40 лет. Насколько истинно предположение, что Х – «старый». Равна ли эта величина 0,5, поскольку Х прожил примерно полжизни, или величины 0,4 и 0,6 более реалистичны. Необходимо решить, какую функцию лучше использовать для отображения возраста в интервал от 0 до 1.

Чем, например, кривая лучше, чем линейная зависимость. Для предпочтения одной формы функции другой нет объективных обоснований, поэтому в реальной задаче будут присутствовать десятки и сотни подобных функций, каждая из которых до некоторой степени является произвольной. Значит в системах, основанных на нечеткой логике, необходимо предусмотреть средства, позволяющие модифицировать функции принадлежности.

6.2. Л. Заде в 1965 году ввел новое понятие нечеткого множества, тем самым расширил класс подмножеств универсального множества .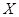

Нечеткое (под)множество A множества 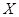определяется через функцию принадлежности 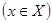- числовой функции со значениями из отрезка [0, 1]. Для некоторого нечеткого множества A значение функции принадлежности трактуется как степень принадлежности точки множеству A.

Если множество 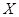состоит из конечного числа элементов то нечеткое множество A можно представить в виде

,

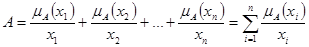где знак «+» не есть сложение, а обозначает совокупность элементов множества (знаменатель) с их принадлежностью (числитель). Следовательно, знак и указанный ниже знак интеграла имеют несколько отличный от традиционного смысл.

В случае непрерывного множества А можно ввести следующее обозначение: .

Для нечетких множеств можно определить следующие стандартные теоретико-множественные операции и отношения:

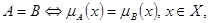
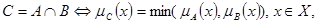
Нечетким отношением R между некоторой проблемной областью (полным множеством X) и другой областью (полным множеством Y) называется нечеткое подмножество прямого произведения 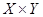, определяемое следующим образом:

,

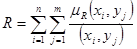где , .

Если существует правило типа «если F, то G», где , то нечеткое отношение R из X в Y определяется как

.

Для свертки нечетких отношений, необходимых при выводах с помощью цепочки правил, выбрана свертка . Пусть R – нечеткое отношение из области X в область Y, а S – нечеткое отношение из области Y в область полного множества Z. Тогда нечеткое отношение из X в Z определяется как свертка

.

6.3. Пусть знания – нечеткие множества . Правило «modus ponens» (правило отделения) для нечетких множеств:

если и , то .

Эта запись имеет существенную особенность: множества 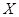и не обязательно совпадают. Есл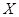и и близки друг к другу, то их можно более или менее сопоставить и получить вывод в сфере их совпадения. Конкретно нечеткие выводы представляют следующим образом.

Прежде всего определим нечеткое отношение из правила . Один из способов определения – как , если есть цепочка из нескольких правил, то отношение – свертка . Вывод определяется из свертки нечеткого множества и отношения : .

Пример 6. Пусть , , , , .

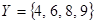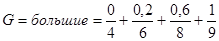Тогда нечеткое отношение R из X в Y для правила 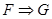определится как

.

Пусть для множеств и , , определены нечеткие множества , .

Тогда ,

.

Пусть далее .

Рассмотрим правило вывода: если 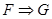и , то . Какое нечеткое множество определяет ?

Множество представим в виде матрицы . Тогда

.

Отсюда , т.е. получаем ответ – «до некоторой степени большое».

Если исходные данные, цели и ограничения плохо поддаются формальному описанию в силу своей природы, то исследование таких систем с применением строгих математических методов вызывает значительные трудности.

Системы, базирующиеся на теории нечеткой логики, являются моделью приближенных рассуждений и выводов. Очень важное место в проблемах принятия решений занимает анализ ситуаций, в которых определяющими являются не количественные, а качественные характеристики. Основным назначением и преимуществом нечеткой логики как раз и является построение формализаций качественных методов исследования.

Дата добавления: 2014-12-17