График 1. 4 страница

Тело можно представить точкой только тогда, ко­гда ее параметры и собственная напряженность несо­поставимы по рангу с параметрами и напряженностью окружающего пространства и тел, образующих структуру данного пространства.

Линия или прямая есть условный след от движения точки (тела) в пространстве. И начало и конец линии входят в поверхность некоторых точек. Линии на уча­стке от поверхности одной точки-сферы до другой имеют конечную длину изменяемой метричности, отождествляемую с некоторой метрической цифрой.

Если эту же прямую продолжить за пределы поверх­ности конечных точек-сфер, внутрь их, то прямая станет иметь бесконечную длину, не отождествимую ни с какими действительными числами.

Линия (условная), соединяющая две движущиеся оп­ределенным образом точки, называется образующим лучом или образующим. Образующий луч индексируется начальной буквой слова — Л. Так, если одна из точек не­подвижна на плоскости, а другая, не меняя расстояния до первой, описывает в движении правильный круг, то образующий луч с такими свойствами в геометрии на­зывается радиусом.

В пространственных системах образующий луч Л всегда подвижен, и каждая его точка в процессе движе­ния описывает геометрическую фигуру, соответствую­щую уравнению движения и коэффициенту связности. Естественно, что в уравнении движения зашифрована и напряженность области концевых точек луча и про­странства, в котором луч движется. (Везде предполага­ется, что след движения остается только от перемеще­ния концевых точек.)

Основной способ движения луча в динамической геометрии — собственное удли­нение или сокращение (пульсация) с

определенным пе­рио-дом, сочетающийся с вращением и некоторым про­странственным переме-щением, например в простран­стве декартовых координат. Поэтому кривые Рис. 10. (следы), плоскости и пространства всех геометрий, включая евк­лидову, Лобачевского и Римана, описываются обра­зующим лучом, один конец которого может двигаться по линии или оставаться неподвижным, а другой, в движении, удлиняться или сокращаться. На рис. 10 показано, как, двигаясь на плоскости, образующий АО от точки А до точки А', остается неизменным по длине и описывает дугу окружности пол­ностью в соответствии с геометрией Евклида. В точке А' он в движении начинает укорачиваться и до точки А" движется по сферической кривой, описывая линию положительной кривизны в соответствии с гео­метрией Римана. В точке А" происходит следующий пе­релом и образующий на участке А" А"' начинает описы­вать линию отрицательной кривизны по геометрии Лобачевского до точки А'", после которой линия движе­ния снова меняет «свою» геометрию и т.д. Переломные точки А', А", А'", А"" имеют статическую для этой об­ласти величину луча, и потому луч может быть отнесен к геометрии Евклида. Перелом есть изменение качест­ва, процесс перехода от одной кривизны к другой.

Оба конца луча могут совершать любые движения, описывать самые различные фигуры, кроме тех, кото­рые могут привести к их пересечению между собой. Так, например, если конец луча, описывающий кривую АА'А"А'"... (рис. 10), замкнется при одновременном движении другого конца-точки О по прямой, то выпи­сывается объемная фигура — профилирован-ный ци­линдр. Если же точка О будет двигаться по окружности, то вместо цилиндра получается тор того же профиля. Таким образом, возникновение искривления как поло­жительного, так и отрицательного, связано с изменени­ем длины луча, создающего это «искривление». Длина луча, в свою очередь, зависит от напряженности про­странства в различных направлениях от точки, из кото­рой он исходит. Изменение напряженности не есть ис­кривление поверхности и не приводит к нему, а вызывает изменение метричности. И, следовательно, длины луча. Покажем это на примере (рис.11).

Пусть луч АО, исходящий из условной точки О, двигаясь по отрезку окружности АВО, начал удлиняться и в точке А' пересек прямую А"О. Продолжая дальнейшее движение, он пересек также прямую ОВ" — окончание дуги АВ.

Дуга АВ разделена прямыми на четыре равных отрезка к, l, т, п. Прямые, разделившие дугу, продолжены до пересечения эквипотенциальной линии А" В" и также делят эту дугу на четыре равных отрезка к", l", т", п". В пространстве отрезки k" = k = l′′ = l = т" = т = п" = п, как следствие пропорционального изменения напряженно­сти от точки О к периферии поверхности. Поскольку пропорциональность напряженности сохраняется на всей поверхности, то отрезок А'В' делится на четыре части к', l′, т', п′ так что: к' = l' = т' = п′ хотя по евклидо­вой и римановой геометрии к' ≠ п′.

Естественно также, что к = к' = к"; l = l' = l"; т = т' = т"; п = п' = п".

То есть все отрезки равны между собой так, что отно­шение каждого из отрезков к длине соответствующего луча между эквипотенциальными дугами будет величи­ной постоянной. Именно это свойство напряженности пространства обусловливает образование пространст­венных ячеек — основных элементов динамической гео­метрии. Напряженность и изменение метричности (кри­визна относительно статичности) — это те факторы, которые не учитывались в теории кривизны ни Гауссом, ни Риманом. Отмечу, что кривизны поверхностей, а тем более кривизны объемов в пространстве не суще­ствует. А поскольку пространство отображает динами­ческую структуру реального мира, то эмпирическое подтверждение ее адекватности этому миру можно по­лучить прямо на поверхности Земли.

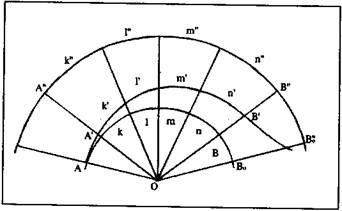
Рис. 11

Приведу описание нескольких экспериментов, под­тверждающих такую возможность. В долине вблизи гор можно построить горизонтальную мерную милю из иде­ального материала длиной в 3 км (с точностью до 1 см). Произвести геодезическую съемку этой мили и перене­сти ее размеры по отвесу на горное плато на высоту одного, а лучше 2 км, и там построить другую горизон­тальную мерную милю той же длины. Современные геодезические приборы позволяют провести операцию переноса на несколько десятков километров с точно­стью до 2-3 см. В соответствии с геометрией Евклида мили и в долине и на плато должны быть разной длины. Миля на плато на высоте 1 км будет на 47 см длиннее мили в долине, а на высоте 2 км – на 94 см.

Следует замерить милю в долине несколькими мер­ными линейками, проведя ими же в аналогичных усло­виях измерение мили на плато, убедиться, что она в точности, до ошибок измерения, равна миле в долине, а, следовательно, мерные линейки изменили свою длину.

Другой эксперимент: на горе с горизонтальным плато на высоте 2 км выложить горизонтально из 40-50 сталь­ных стержней длиной по 20-25 м (± 0,1 мм) единый стержень километровой длины. Отметки его концов пе­ренести по отвесу в долину под горой, потом разобрать конструкцию, перебросить ее в долину и вновь собрать. Согласно геометрии Евклида собранная конструкция будет короче отметок на 32 см. Однако стержни при из­мерении метром окажутся в рамках отметок ± ошибка измерения.

Наконец можно просто провести геодезическими при­борами измерение отрезка относительно горизонталь­ной поверхности в долине на длине 10 км и, замерив та­кую же длину, перенесенную по отвесу на плато на высоту 2 км, убедиться с достаточно грубым приближе­нием (± 25-30 см) в исчезновении при измерении отрез­ка почти трехметровой длины. (Можно предположить, что аналогичные нестыковки уже встречались карто­графам и геодезистам и не получали теоретического объяснения.)

Рассмотрим в общих чертах структуру пространст­венной ячейки отграниченной нейтральными зонами. Пространственные первичные ячейки образуются ядра­ми по периметру своей нейтральной зоны, соизмеримые по напряженности с напряженностью окружающего пространства. Они могут включать одно ядро (редко), два ядра (большинство), несколько ядер (редко). В настоящей работе напряженность схематически обознача­ется условной линией, как бы оставляемой ядром тела, взаимодействующего с пространством. Эти линии по наглядности являются некоторым подобием фарадеевых силовых линий, а в геометрии это геодезические линии. Прямые напряженности выходят из пространства одного ядра 1(рис 12) с фиктивным центром О и входят в пространство другого ядра 2 с фиктивным центром О₂. Линии напряженности О₁АО₂, О₁ВО₂, О₁СО₂..., соеди­няющие фиктивные центры, в пространстве параллель­ны. В точках А, В, С, D,... они испытывают кажущееся преломление, обусловленное зоной единой минималь­ной напряженности — нейтральной или эквипотенциаль­ной зоной.

Ячейка образуется только тогда, когда оба ядра имеют пространственную линию общей эквипотенциальной зоны (нейтральные зоны), как бы выделяющую их из окружающего пространства. Эти зоны образует из них единую систему и не позволяет ядрам покинуть ее. Именно она обусловливает дискретность пространства одного ранга.

Первичные ячейки через нейтральные зоны взаимо­действуют с окружающими ячейками и входят в состав ячеек несоизмеримого

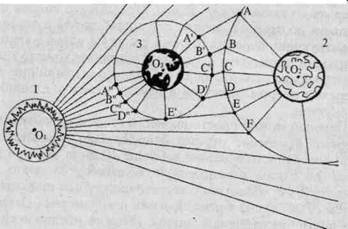
Рис. 12

ранга. Общая структура про­странства ¾ иерархия равенства. В пространстве ячей­ки между ядром и нейтральной зоной могут существо­вать спутники ядра 3с центром О₃. Между спутником и ядром также существует нейтральная зона А'В'С... А"В"С", охватывающая спутник эллиптической сферой. Выходящие из центра О₁ линии входят в центр О₃ или замыкаются в нейтральной зоне. Радиус (статический) спутника определяется граничными условиями. Про­странство ячейки, ядра и спутника всегда находятся в движении.

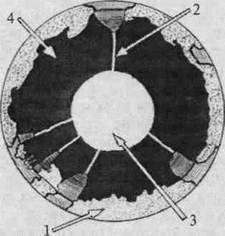
Ядро как элемент ячейки и самостоя­тельная система единой внутренней напряженности име­ет сложную струк­туру, обусловлен­ную материально­стью самого образо­вания. Оно включа­ет несколько «скорлуп»-сателлитов 1 (рис. 13), у которых нейтральная зона 2 каждой скорлупы находится либо вну­три этой поверхно­сти, либо у самой поверхности, что и удерживает их в единой системе. Поэтому сферы сателлитов, взаимодействуя нейтраль­ными зонами, образуют на своей внешней поверхности равновеликую напряженность, интегрированную уже как напряженность самого ядра. Пространство внутри скорлуп Рис. 13. (рис. 13) материально и имеет напряженность более высокого ранга, чем снаружи. В этом про-странст­ве может находиться внутреннее вещественное ядро-керн 3. Его напряженность несоизмерима по рангу ни с напряженностью пространства ячейки, ни с напряжен­ностью сателлитов. Она есть плотность другого ранга.

Геометрия свойств здесь о свойствах как элементах геометрии

2.3. Свойства пространственных систем

Рассмотрим, что неявно происходит с пространством при возникновении в нем тел, отображаемых элемента­ми динамической геометрии [28]. Возьмем чистый лист бумаги и предположим, что этот лист есть некоторая плоскость, однородная и изотропная в четырех направле­ниях, а, следовательно, на пространстве листа мы не за­мечаем никакой структуры и внутренней напряженно­сти. Эта поверхность может быть названа бес­форменной, хаотичной, или поверхностью одного ранга. Структура этого ранга и его ячейки нами не фиксируют­ся.

Поставим в любом месте листа точку. Точка на листе никакой роли не играет, структуры не создает, и как бы не возникает напряженности различной плотности на всей поверхности. Но хаос уже исчез, точка изменяет качество всего пространства и становится центром образования нового пространства, центром структуризации и изменения его качеств, центром дру­гого ранга. И не существенно, пространство ли это лис­та или пространство космоса, в котором имеется тело. Существенно в подходе к явлению, к его формализации ¾ другое. Образует ли точка пространство актуальной бесконечности или бесконечности потенциальной? Именно одна из сторон двойственности обусловливает процесс понимания формализации элементов различных пространств по мере их воссоздания на листе.

Точка, как и другие элементы в пространстве потен­циальной бесконечности (или в объеме), не равнозначна другим не видимым на листе точкам и уже создает (да­же если это не отражают условия задачи) в окружающем пространстве некоторую напряженность, определяемую изменением метрического пространства. Именно метричность есть агент, отображающий распространение плотности напряженности от точки в пространстве. При этом на бесконечности одного ранга плотность убывает от точки до нуля. (Нулевая плотность напряженности равна напряженности, создаваемой телами нижнего ран­га и потому не равна 0.) Поскольку значимость точки определяется ее рангом и рангом пространства, то ранги определяют также изменение метричности.

Если на плоскости (в пространстве) имеется две или несколько точек, то напряженность между ними опре­деляется рангом точек. Поскольку в задачах чаще всего задается одинаковый ранг, то плотность напряженности между точками становится неоднозначной. Но между ними всегда имеется зона одинаковой плотности напря­женности — нейтральная зона. Структура всех напря-женностей между точками определяется именно харак­тером и местом нейтральных зон. В плоскости (как и в объеме) актуальной бесконечности напряженность от­сутствует, а следовательно, может отсутствовать и метричность (что и наблюдается в проективной геометрии). Если же она присутствует, то неизменна величиной по всей плоскости (по всему объему), и точка, как и другие фигуры в этом пространстве, на пространство никакого влияния не оказывает.

Поставим еще одну точку. Структуризация возросла и снова изменилось качество всего пространства. Между точками по различным критериям может быть найдена активная область или нейтральная зона, разде­ляющая как их, так и плоскость листа. Или они могут быть соединены одной линией, которая делит лист уже на две иные, чем нейтральная линия, части, создавая иные пространства по обе ее стороны.

Соединим точки линией, и в одном из образовавшихся пространств в стороне от линии поставим точку, создав тем самым все необходимые предпосылки для форму­лирования или пятой аксиомы Евклида или основной аксиомы динамики пространства. Все имеющиеся на плоскости элементы равнозначны или, по современной артикуляции, равноправны, и только движение опреде­ляет их принадлежность к динамике. Если теперь со стороны прямой, восстановив до точки М образующий луч, двигать его неизменным по длине вдоль прямой, то точка, в которую он вошел, будет оставлять след евкли­довой прямой, параллельной базовой. И это будет про­должаться бесконечно, если... если мы не последуем за Дезаргом. Дезарг, исходя из кажущегося пересечения в перспективе параллельных в одной точке, предложил считать пересечения проекциями «бесконечно удален­ных» точек, равноправными со всеми остальными эле­ментами. Так, в проективную геометрию вошли «несоб­ственные (бесконечно удаленные) точки» и «несобст­венные плоскости» — плоскости, на которых лежат эти точки.

Введение «несобственных» точек и плоскостей нарушило равнозначность элементов геометрии, было пер­вым качественным отображением на плоскости фак­торов напряженности пространства и свидетель­ствовало о другом ранге несобственных точек. Однако нарушения равнозначности элементов обнаружено не было, и не потому, что оно отсутствует, а потому, что и обычным, и несобственным точкам и площадям постулировали равноправие. Это постулирование рав­ноправия обусловило полную статичность проективной геометрии, нивелировало напряжен-ности, привело к тому, что все прямые одной плоскости Дезарга всегда пересекаются на бесконечности. Таким образом, во­прос о различной напряженности у точек и линий на плоскости даже не возник. Развитие получили аксиомы статической геометрии.

Если теперь, для примера, представить движение колес паровоза по рельсам в пространстве обычном и не­собственном (потенциальной бесконечности), то мы увидим, как бы следуя за ним неизменными, что рельсы сначала будут параллельными (расстояние между ними — образующий луч, остается неизменным). Затем под воздействи­ем возрастающей напряженности несобственного про­странства начнут сходиться (образующий луч будет уменьшаться и, соответственно, паровоз тоже), и, по­дойдя к несобственной точке, луч станет по «длине» меньше ее. Пройдя поверхность сферы-точки, т.е. про­никнув в объем другого ранга, луч продолжает умень­шаться и, миновав центр (но не через него), начинает возрастать до противоположной поверхности сферы.

Поскольку напряженность поверхности вокруг точки сферически симметрична (в предположении, что точка находится вдали от других точек), по выходу из несоб­ственной точки луч начнет расширяться, а рельсы, сле­довательно, расходиться под тем же самым углом, под которым они сходились. В результате возникнет полная иллюзия того, что в несобственной точке произошло пе­ресечение рельсов. На самом деле, на всем протяжении движения к точке, сквозь нее и за ней рельсы оставались параллельными. Менялась же напряженность несобст­венного пространства и несобственной точки в полном соответствии с динамикой пространства, что и создава­ло иллюзию схождения и расхождения рельсов. (Иллюзию их пе­ресечения в одной точке.)

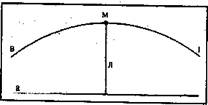
Вторично неявная напряженность геометрической по­верхности проявила себя в геометриях Лобачевского и Римана. Это станет особенно заметно, если луч Л, вхо­дящий в точку М из прямой а, начинает двигаться вме­сте с точкой М на бесконечность, например в правую сторону (рис. 14). Причем граничные условия аксиомы запрещают точке приближение к прямой а, а лучу — со­кращаться по длине, но не запрещают точке М удалять­ся, а лучу Рис. 14.

Л удлиняться (своего рода пространственное отталкивание). Поэтому по мере движения точка начи­нает отклоняться от прямой — ветвь в'. Если же луч Л вместе с точкой будет двигаться в левую сторону, то получим анало­гичное откло-нение от прямой а — ветвь в. Фигура, образуемая обеими ветвями как бы единой прямой в, окажется не эквидис-тантой, а некото­рой седловиной образуемой двусторонним движением.

В этом построении начинает проявляться физический смысл движения, и получается, что точка М замыкает на себя две само­стоятельные ветви прямой в, разрывая ее и имея статус несобственной точки (точки одного ранга с прямой). Отсюда также следует, что пространство, в котором двигаются прямые, анизотропно. А потому луч Л, дви­гаясь от точки в любую из сторон, будет изменять свою длину пропорционально изменению напряженно­сти пространства и движущейся точки. И также про­порционально этой напряженности будет меняться метричность отрезков по длине прямой вМв'.

Если же граничные условия (формулировка Римана) препятствуют отклонению ветвей в и в ' от прямой а при движении в обе стороны от точки М, то ветви, переме­щаясь на бесконечность, будут приближаться к прямой а (рис. 15). Таким образом, граничные условия не по­зволяют образующему лучу в движении удлиняться, ос­тавляя ему возможность сокращения. И в этих условиях луч Л выписывает подобие эллиптической кривой (сво­его рода пространственное притяжение). Однако конеч­ные точки ветвей в, в' имеющие ранг прямой а, никогда не пересекут ее. И кривая вМв' никогда не будет иметь общей точки с прямой а. Она не замкнута.

Подобие линии вМв' эллиптической кривой послу-жи­ло основанием для наречения римановой геомет-рии «сферической» и завуали-ровало как существование

Рис. 15. на­пряженности пространства, так и разрыв кривой в точке М. Поэтому образованная данной кривой, при вращении ее вокруг а, сферическая поверхность не может считать­ся истинной сферой и потому, что след точки М несет в себе момент нестыковки ветвей в и в', и потому, что эта "сфера" оказываетсянезамкнутой с линией а, и потому, что внутри "сферы" остается элемент образующей ее структуры — прямая а.

Напряженность, выражаемая элементами геометрии в виде неравноправных, несобственных точек и линий, по-видимому, снимается введением в геометрию поня­тия абсолюта — такой геометрической фигуры, которая остается неизменной при любых преобразованиях дан­ной подгруппы. Следовательно, абсолютом считается элемент, ранг собственной напряженности которого выше остальных элементов данной плоскости. И все преобразования, изменяющие форму остальных элемен­тов (и их напряженность), не в состоянии изменить на­пряженность абсолюта.

Таким образом, понятие абсолюта окончательно за­крыло в геометрии все направления возможного описа­ния реального мира в терминах напряженности, движе­ния, взаимодействия. Геометрия стала чисто статиче­ским описанием только одной актуальной бесконеч­ности.

Попробуем в самой эскизной форме резюмировать не­которые первичные понятия и свойства элементов ди­намического пространства. Прежде всего, отметим важ­нейшую роль познания потенциальной бесконечности. Бесконечность как понятие высшая форма абстраги­рования. Представление об осуществимости абст­рактного движения в бесконечность приводит к противоречию с проявлением неопределенности и недости­жимости в отдалении от нашего сознания. Движение в бесконечность оказывается абстракцией, связанной с возможностями качественного изменения дискретного пространства с переходом от пространства одного ранга к пространству другого ранга. Именно ранжиро­вание бесконечностей по уровням определяет соизме­римость или несоизмеримость пространственных обра­зований или отрезков прямых.

Иерархическая равнозначность ранговых структур по их положению и естественное взаимодействие при дви­жении определяет дискретность и непрерывность обра­зуемого ячейками пространства плоскости или объема. Ячеистое поле пространства само для себя и для своего ранга дискретно, а для верхнего ранга непрерывно и но­сит полевой характер. Динамическое пространство все­гда не пусто.

Естественный смысл бесконечности заключается в ее количественной и качественной незавершенности. Это выражается, в частности, через изменение метричности в сопоставлении с метричностью статической геометрии. Каждый последующий шаг всегда отличен от предыдущего качественно и количественно.

Как только вводится понятие бесконечного простран­ства, т.е пространства имеющего другое качество, и элементы геометрических фигур устремляются в бесконечность (например, пятая аксиома в формулировке Евклида), тем самым в статическую геометрию неявно вводятся новые, не присущие ей качест­ва (движение, недостижимость бесконечности, неопределенность, время, вза­имодействие и т.д.). И эти качества коренным образом изменяют поведение геометрических элементов и пространства, которое описывается ими. Эти качества приводят к взаимосвязи всех элементов движения и геометрическая статическая общность точек, отрез­ков, плоскостей, объемов сразу наполняется физиче­ским содержанием и становится разделом физики; системной общностью. Общностью, в которой ни одна точка, ни одна фигура ни в одном месте пространства не обладает истинной самостоятельностью, остава­ясь в то же время равновеликой по значимости и взаи­модействию со всеми фигурами и пространством. И всякое ее движение в любом направление этого про­странства будет сопровождаться изменением ее гео­метрических (статических) параметров пропорцио­нально напряженности самого пространства. Однако динамические (физические) параметры этой общности останутся неизменными. И эти качественные проти­воречия изменяемости и неизменности параметров в статическом и динамическом состояниях тоже неявно заложены в пятую аксиому Евклида.

Имеются неоднозначности и в соизмеримости рас­стояния в пространстве между двумя произвольными точками А и В. Хотя оно и в одном и в противополож­ном направлении количественно равно (понятие рас­стояния применено здесь по аналогии с Евклидом), но не эквивалентно и потому не отвечает требованиям рефлективности, симметрии и транзитивности (следст­вие неоднородности и анизотропности пространства), оно не может быть взято безотносительно времени и плотности, которые в неявном виде присутствует в каж­дой области пространства.

Перенос отрезков или фигур параллельно своему по­ложению вдоль замкнутого контура вызывает их посто­янное самотождественное изменение, но в результате обхода контура конечная фигура совпадет с первичной. В пространстве отсутствуют малые поверхности и объ­емы (относительно измерителя), и перенос фигуры или мерного инструмента из одного пространства в другое вызывает изменение длины мерных инструментов (от­носительно статики) пропорционально напряженности внешнего поля данного пространства. Сумма же углов треугольника и на поверхности сферы, и в объеме все­гда равна 2 π. Эта особенность исключает возможность определения разницы в геометриях. Отличительная особенность динамического пространства и образованного им пространства — детерми­низм. Именно каузальность порядка причина-следствие определяется коэффициентом связности и золотым мно­гообразием.

Рассмотрим основные фигуры пространства. Все ма­териальные образования одного ранга, кроме продуктов катастроф, стремятся приобрести форму сферы. Сферы одного пространства обладают следующими качества­ми:

• все, сферы построенные вокруг отсутствующего единого центра, равны. Их эквипотенциальная поверх­ность состоит из бесчисленного количества ячеек, а ра­диус имеет бесконечную длину;

• каждый отрезок исходит из точки и входит в другую точку. Однако их можно продолжить по прямолинейной поверхности сферы до исходящего отрезка и считать непрерывными;

• сферы всегда ядра и на плоскости и в пространстве различаются по рангу. Сферы более «низкого» ранга могут считаться точками. Точка — это всегда матери­альная сфера, не имеющая центра.

Точка — ядро, структура которого несоизмерима по рангу с пространством, в котором она находится, и влияющая на это пространство. Внешняя поверхность отграничивает ее от пространства. Точка всегда беско­нечна вглубь. Точка на прямой или в пространстве и луч из нее — это отделение соизмеримой области простран­ства (внешняя часть образующегося луча) от несоизме­римой (части, устремленной к центру точки).

Все точки одного ранга неравнозначны по количест­венным величинам всех качеств и в первую очередь по напряженности. Поэтому метрика координатных осей с центром в любой окрестности точки, кроме ядра, бу­дет различной (относительно статического эталонного метра).

Ячейка (две или более) — взаимосвязанные напряжен­ностью собственного поля сферические структуры (яд­ра), несоизмеримые по размерам с расстояниями между ними, входящие в единую внешнюю эквипотенциаль­ную нейтральную зону. Все пространство — «пена» взаимосвязанных первичных ячеек.

Линия (прямая) — абстракция — последовательность расположенных в одном направлении несоизмеримых с пространством ячеек. Линия всегда дискретна. Дискрет­ность обусловлена наличием бесконечных (вглубь) то­чек на ней. Непрерывной она может быть только мыс­ленно.

Поверхность (плоскость) — многообразие распростра­няющихся в двух направлениях дискретных ячеек.

Объем — область, образованная состоянием взаимо­связанных ячеек, отграниченная от других областей своей нейтральной зоной. Существование нейтральных зон определенной напряженности обусловливает свой­ства каждого из тел

2.4. Геометрия золотых пропорций

Откуда пришли представления о делении отрезков в крайнем и среднем отношении, позволяющем получать золотое число Ф и образующие пропорцию, названную Леонардо да Винчи «золотым сечением», неизвестно. Ho в Древней Греции на основе золотого числа Ф = 1,618 получали ряд из 11 чисел посредством последова­тельного умножения базисной 1 на Ф (восходящая ветвь ряда) и делением базисной 1 на Ф (нисходящая ветвь ряда), имеющий название золотого ряда и бесконечный, при продолжении, в обе стороны:...; 0,034; 0,056; 0,090; 0,146; 0,236; 0,382; 0,618; 1,000; 1,618; 2,618; 4,236;... и т.д. (египетский ряд [28 ]). Каждое число этого ряда представляет собой иррациональную (бесконечную) по­следовательность цифр, округленных до 4 знаков. Како­во собственное значение этих чисел, и к какой геометрии они относятся — неизвестно тоже, а потому числа эти стоят на обочине и геометрии и физики.

Дата добавления: 2014-11-29