Спецификация эконометрической модели

Метод оптимального выбора объясняющих переменных

Заметим, что 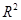возрастает при добавлении еще одного регрессора, что не всегда означает улучшение качества модели. Чтобы устранить этот эффект, используется скорректированный :

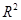. (1)

В нашем случае:

Отметим, что

, (2)

Наилучшей считается модель с наибольшим .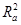

Строятся модели вида:

,

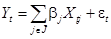где , .

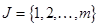Алгоритм выбора .

1-й шаг

Рассматриваются модели вида:

при всевозможных .

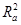Находится независимая переменная , для которой максимально.

Обозначим индекс этой переменной через .

Обозначим:

,

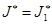
Обозначим через значение показателя 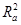для оптимальной модели, полученной на первом шаге.

k -й шаг

Рассматриваются модели вида:

при всевозможных .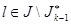

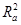Находится независимая переменная , для которой максимально.

Обозначим индекс этой переменной через .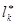

Обозначим:

Обозначим через значение показателя 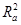для оптимальной модели, полученной на данном шаге.

Далее сравнивается c .

В случае :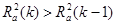

1) модель считается лучшей, чем модель , и полагается ;

2) если 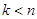(т.е. не все переменные включены в модель ), осуществляется переход к следующему шагу (т.е. значение 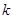увеличивается на единицу)

3) если 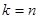, то на этом заканчивается процесс выбора оптимальной модели; в этом случае все переменные включены в оптимальную модель.

В случае , оптимальной считается модель и на этом заканчивается процесс выбора оптимальной модели.

Пример 5

Данные о рыночной цене коттеджей, а также об их площади, вместимости гаража и количестве комнат приведены в табл. 3. Требуется построить линейную регрессионную модель для оценки рыночной стоимости коттеджей.

Наблюдения	Площадь	Гараж	Спальни	Цена
	1,1
	1,15
	1,4
	1,7
	1,8
	1,9
	1,9
	2,1
	2,1
	2,3

1-й шаг

Строим модели: , , и для них находим .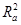

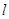
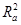
	0,8554
	0,7317
	0,7703

Максимальное значение 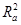на 1-м шаге 0,8554 при .

Итак, , ,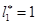

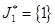На первом шаге выбрана модель:

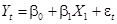
и полагается

2-й шаг

Строим модели: 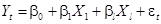, , 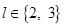и для них находим .

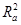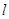
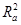
	0,9239
	0,8466

Максимальное значение 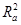на 2-м шаге 0,9239 при .

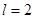Итак, , ,

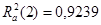
Сравниваем 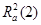и .

Поскольку , модель лучше модели .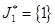

Следовательно, на втором шаге выбирается модель :

и полагается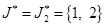

3-й шаг

Строим модель: 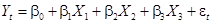и для нее находим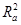

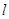
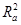
	0,9179

Значение 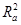на 2-м шаге 0,9179 при .

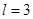Итак, , ,

Сравниваем и .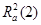

Поскольку , модель, полученная на 2-м шаге, считается лучше модели, полученной на 3-м шаге.

Следовательно, в качестве оптимальной выбирается модель :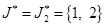

.

Методы выбора вида зависимости

В общем случае регрессионная модель имеет вид:

, (3)

где .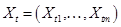

Функция не обязательно линейна относительно 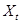, и зависит от вектора параметров . Следовательно,

, (4)

Заметим, что часто число параметров совпадает с числом объясняющих факторов 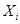, т.е. . (Если , можно считать, что .)

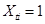Для получения оценок 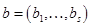коэффициентов можно использовать МНК:

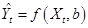(5)

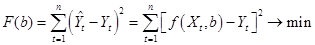(6)

Затем можно рассчитать скорректированный коэффициент детерминации в соответствии с формулой (1):

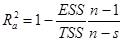(7)

и на основе этого коэффициента выбрать оптимальный вид модели и произвести оптимальный отбор значимых объясняющих факторов. (Вначале рассмотреть несколько видов функции , для них произвести оптимальный отбор объясняющих факторов, и выбрать вид функции с наибольшим .)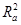

Отметим, что одним из способов решения оптимизационной задачи (6) является использование условий первого порядка:

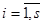, (8)

т.е. решение системы вообще говоря нелинейных уравнений (8).

Сведение нелинейной регрессии к линейной

Часто представляется возможным свести нелинейную регрессию вида:

(9)

к линейной.

Логарифмическая (лог-линейная) модель

Пусть исходная модель – показательная:

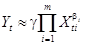(10)

Экономический смысл.

Из (10):

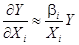(11)

Отсюда:

. (12)

В силу (12) – эластичность фактора по фактору 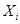, т.е. показывает процентное изменение при увеличении 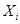в расчете на 1%.

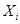Следовательно, модель (10) целесообразно использовать, если есть основания полагать, что эластичности постоянны, т.е. при равных относительных изменениях фактора относительные изменения фактора также (приблизительно) равны.

Прологарифмировав соотношение (10), получим:

, (13)

или:

. (14)

Модель (14) – это так называемая двойная логарифмическая модель (и зависимая, и объясняющие переменные заданы в логарифмическом виде).

Введя обозначения: 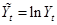, , 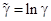получим линейную модель:

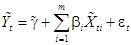(15)

относительно новых переменных и .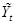

Полулогарифмические модели

Пусть

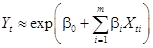(16)

Из (16):

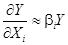(17)

Отсюда:

(18)

Следовательно, показывает относительное изменение фактора при увеличении фактора 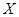в расчете на одну единицу. (Умножив на 100 получим процентное изменение при увеличении 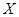в расчете на одну единицу.)

Эту модель целесообразно использовать, если есть основания считать, что при равных абсолютных изменениях фактора 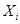относительные изменения фактора также (приблизительно) равны.

Прологарифмировав (16), получим:

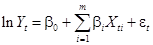(19)

или

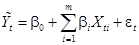, (20)

где .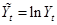

Пусть

(21)

Из (21):

(22)

Отсюда:

(23)

Следовательно, 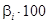показывает абсолютное изменение фактора при увеличении фактора 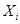в расчете на 1%.

Эту модель целесообразно использовать, если есть основания считать, что при равных относительных изменениях фактора 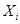абсолютные изменения фактора также (приблизительно) равны.

Модель (21) сводится к следующей линейной модели:

, (24)

где .

Отметим, что любая модель вида:

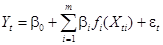(25)

сводится к линейной модели:

(26)

где .

Например, модель (25) может иметь вид:

(обратная модель) (27)

либо

(степенная модель) (28)

Качественные переменные

Например, при исследовании зависимости зарплаты от различных факторов может возникнуть вопрос, влияет ли на ее размер, и если да, то в какой степени, наличие у работника высшего образования.

Введем переменную , описывающую наличие у работника высшего образования

Положим:

(29)

Переменная описывает качественный признак, а не количественное значение.

Такие переменные называются качественными.

Обычно качественные переменные принимают только два значения: 0 и 1. Принято считать, что качественная переменная равна 1 в случая наличия признака, и 0 – в случае его отсутствия. Такие переменные также называются бинарными, двоичными, логическими. В англоязычной эконометрической литературе их называют “dummy variables”, что на русский язык часто переводится как “фиктивные переменные.”

Пусть модель имеет вид:

, (30)

где 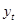размер зарплаты работника, – влияющие на нее факторы, – качественная переменная, описывающая наличие у работника высшего образования, 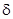– коэффициент регрессии.

Методика работы с моделью вида (31) такая же, как и для любой линейной регрессионной модели. Экономический смысл коэффициента регрессии 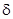состоит в том, что этот коэффициент показывает насколько заработная плата работника с высшим образованием в среднем отличается от заработной платы работника без высшего образования с такими же значениями других объясняющих факторов.

Если включаемый в рассмотрение качественный признак имеет не два, а несколько значений, используют несколько бинарных переменных. Типичным примером подобной ситуации является исследование сезонных колебаний. Пусть, например, 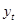– объем потребления некоторого продукта в месяц 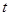, и есть основания считать, что потребление зависит от времени года. Для выявления влияния сезонности можно ввести четыре бинарные переменные , , , :

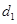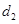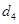(32)

(33)

(34)

и оценивать уравнение:

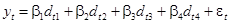. (35)

Коэффициенты , , 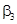и показывают среднемесячное потребление продукта, соответственно, для зимних, весенних, летних и осенних менсяцев.

Отметим, что модель (35) можно также записать в виде:

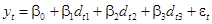(36)

Коэффициент в уравнении (36) показывают среднемесячное потребление продукта для осенних месяцев, – для зимних, – для весенних, – для летних. Таким образом, коэффициенты , и 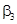показывают средние сезонные отклонения в объеме потребления зимних, весенних и летних месяцев по отношению к осенним месяцам.

Отметим, что ввиду присутствия в (36) свободного члена мы не вводим в (36) четвертую бинарную переменную 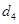, относящуюся к осени, иначе тогда для любого месяца 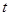выполнялось бы тождество 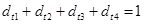, что означало бы линейную зависимость регрессоров в (36), и как следствие, невозможность получения МНК-оценок. (Напомним, что матрица 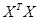должна быть не вырождена.)

Ситуация, когда при наличии в уравнении регрессии свободного члена сумма фиктивных переменных равна константе, называется “dummy trap”. При построении уравнения регрессии с качественными переменными следует обращать внимание на возможность такой ситуации.

Фиктивные переменные позволяют строить и оценивать так называемые кусочно-линейные модели, которые можно применять для исследования структурных изменений.

Пусть, например, 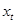–размер основного фонда в период 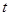, 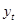– объем продукции, выпущенной в этот же период. Из некоторых априорных соображений исследователь считает, что в момент произошла структурная перестройка и линия регрессии будет отличаться от той, что была до момента , но общая линия остается непрерывной.

Чтобы оценить такую модель, введем бинарную переменную , полагая, что

(37)

и запишем регрессионное уравнение:

(38)

Регрессионная линия, соответствующая (38), имеет коэффициент наклона для и для 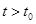, и разрыва в точке 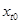не происходит. Таким образом, тестируя гипотезу , мы проверяем предположение о том, что фактически структурного изменения не произошло.

Дата добавления: 2014-12-17