Основная теорема о линейной независимости

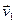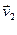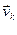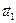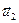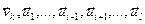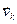
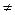
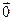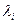
Лемма 3.10. Пусть система векторов , ,…, (1) линейно независимая и выражается через , ,…, (2) тогда 1) система векторов -линейно зависимая; 2) система (1) линейно выражается через (6) при некотором і. Доказательство. 1) Система (1) выражается через (2), значит выражается через (2). Значит - лин. завис. 2) Из п. 1) следует, что , где не все λ = 0. Так как , 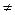0, значит 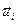выражается через 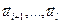, из чего следует, что система (2) выражается через (6), и по 3.3 система (1) выражается через (6).■

Т. 3.11. (основная теорема о линейной независимости) Когда линейно независимая система (1) выражается через систему (2), тогда k 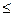L, т.е. в ней не может быть больше векторов, чем в той, через которую они выражаются. Доказательство. По Лемме 3.10. из (2) можно удалить некоторый вектор, дополнить ее векторам из (1) и получить систему, через которую выражается (1). Пусть мы несколько раз провели эту операцию и получили систему (7) (без потери общности). По 3.10 из (7) можно удалить вектор, дополнить ее векторам и получить систему, через которую выражается (1). Покажем, что возможно удалить некоторый из векторов По 3.10 - линейно зависимая система, 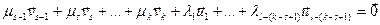, где не все коэффициенты равные нолю. Невозможно чтобы все λ были равные нолю, так как система (1) линейно независимая, значит ее подсистема 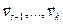- линейно независимая, из чего следует, что , тогда, как в доказательстве 3.10, можно удалить .Так будем делать, пока не получим, что s=L.■

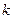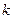
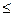
Вывод 3.12. Когда система (1) линейно выражается через (2) и > , тогда (1) - линейно зависимая. Доказательство. Когда бы (1) была линейно независимою, тогда по 3.11 имели бы, что , а это противоречить условию.■

В ывод 3.13. Средь линейных комбинаций векторов из (2) не более линейно независимых.

Доказательство. Очевидно из 3.12.■

ВЫВОД 3.14. Когда (1) и (2)- две линейно независимые системы векторов, (1) выражается через (2) и (2) выражается через (1), тогда Доказательство. По 3.11 і 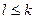, значит .■

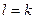Дата добавления: 2014-11-29