Тема 2. Точечное оценивание

План.

1. Параметрические статистические модели. Точечные оценки. Несмещенность оценки. Состоятельность оценки. Эффективность оценок.

2. Оценка математического ожидания. Несмещенная оценка дисперсии.

1.

Все задачи математической статистики можно разбить на две группы: параметрические и непараметрические. Если известны вид распределения и область изменения параметров, то имеют место параметрические задачи. Например, если известно, что изучаемая случайная величина распределена в совокупности нормально, то необходимо оценить математическое ожидание а и среднее квадратическое отклонение σ², так как эти параметры полностью определяют нормальный закон распределения. Если же закон распределения неизвестен, то речь идет о непараметрической задаче.

Очень часто в приложениях рассматривают именно параметрическую модель. В этом случае предполагают, что закон распределения генеральной совокупности принадлежит множеству {F(x;θ):θ 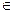Θ}, где вид функции распределения задан, а вектор параметров θ неизвестен. Требуется найти оценку для θ (приблизительное значение искомого параметра) или некоторой функции от него (например, математического ожидания, дисперсии) по случайной выборке (Х1,Х2,…Хn) из генеральной совокупности Х.

Определение. Оценкой θ_n параметра θ называют всякую функцию результатов наблюдений над случайной величиной Х (иначе – статистику), с помощью которой судят о значении параметра θ: θ_n=θ_n(Х1,Х2,…,Хn).

Т.к. Х1,Х2,…Хn – случайные величины, то и оценка θ_n (в отличие от оцениваемого параметра θ – величины неслучайной) является случайной величиной, зависящей от закона распределения случайной величины Х и числа n.

Существуют два вида оценок: точечные и интервальные. Рассмотрим точечные оценки.

Определение. Точечной оценкой θ* параметра θ называется числовое значение этого параметра, полученное по выборке объема n.

Пусть Х_n =(Х1,Х2,…Хn) – случайная выборка из генеральной совокупности Х, функция распределения которой известна F(х,θ), а θ – известный параметр, т.е. рассматривается параметрическая модель. Требуется построить статистику θ*_n которую можно было бы принять в качестве точечной оценки параметра θ. В общем случае необходимо дать ответ на вопрос: какими свойствами должна обладать статистика θ*_n, чтобы она была в некотором смысле наилучшей оценкой параметра θ. Основное условие, которому должна удовлетворять наилучшая оценка, это, например, математическое ожидание квадрата отклонения оценки от оцениваемого параметра должно быть по возможности меньшим.

Рассмотрим наиболее важные свойства оценок.

Определение. Оценка θ*_n параметра θ называется несмещенной, если ее математическое ожидание равно оцениваемому параметру, т.е., М(θ*_n)=θ.

В противном случае оценка называется смещенной.

Это свойство желательно, но необязательно. Требование несмещенности гарантирует отсутствие систематических ошибок при оценивании.

Хотя каждая отдельная оценка лишь в редких случаях совпадает с соответствующей характеристикой генеральной совокупности, при «аккуратном» оценивании многократное осуществление выборок одного объема n обеспечивает совпадение среднего значения оценки по всем выборкам с истинным значением оцениваемого параметра. Разность М(θ*_n)-θ называется смещением или систематической ошибкой оценивания. Для несмещенных оценок систематическая ошибка равна 0.

Свойство несмещенности оценки является важнейшим, но не единственным. Порой существует несколько возможных оценок одного и того же параметра. Какая из них лучше? Очевидно, выбор будет сделан в пользу той из них, вероятность совпадения которой с истинным значением оцениваемого параметра выше. Оценка должна иметь такую плотность вероятности, которая наиболее сжата вокруг истинного значения оцениваемого параметра, т.е., в этом случае она должна иметь наименьшую среди других оценок дисперсию.

Определение. Несмещенная оценка θ*_n параметра θ называется эффективной, если она имеет наименьшую дисперсию среди всех возможных несмещенных оценок параметра θ, вычисленных по выборкам одного и того же объема n.

Эффективность оценки θ*_n определяют соотношением , где 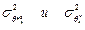– соответственно дисперсии эффективной и данной оценок. Чем ближе e к 1, тем эффективнее оценка. Если 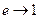при n 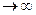, то такая оценка называется асимптотически эффективной.

Определение. Оценка θ*_n параметра θ называется состоятельной, если она удовлетворяет закону больших чисел, т.е. сходится по вероятности к оцениваемому параметру:

.

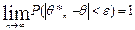Другими словами, состоятельной называется такая оценка, которая дает истинное значение при достаточно большом объеме выборки вне зависимости от значений входящих в нее конкретных наблюдений. Свойство состоятельности является обязательным для оценки.

В большинстве случаев несмещенная оценка является и состоятельной. С другой стороны, состоятельные оценки с увеличением объема выборки будут приближаться и лежать все плотнее к истинному значению. Это указывает на асимптотическую несмещенность состоятельной оценки. Поэтому при невозможности получения несмещенной оценки целесообразно найти хотя бы состоятельную оценку.

В качестве статистических оценок параметров генеральной совокупности желательно использовать оценки, удовлетворяющие одновременно требованиям несмещенности, состоятельности и эффективности. Однако этого достичь не всегда удается. Может оказаться, что для простоты расчетов целесообразно использовать незначительно смещенные оценки или оценки, обладающие большей дисперсией по сравнению с эффективными оценками, и т.п.

2.

Несмещенной оценкой генеральной средней (математического ожидания) служит выборочная средняя ,

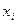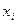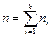где - варианта выборки; - частота варианты ; - объем выборки.

Замечание 1. Если первоначальные варианты 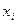- больше числа, то для упрощения расчета целесообразно вычесть из каждой варианты одно и то же число С, т.е. перейти к условным вариантам (в качестве С выгодно принять число, близкое к выборочной средней; поскольку выборочная средняя неизвестна, число С выбирают «на глаз»). Тогда

.

Смещенной оценкой генеральной дисперсии служит выборочная дисперсия

;

Эта оценка является смещенной, так как

.

Более удобна формула

.

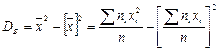Замечание 2. Если первоначальные варианты 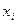- больше числа, то целесообразно вычесть из всех вариант одно и то же число С, равное выборочной средней или близкое к ней, т.е. перейти к условным вариантам (дисперсия при этом не изменится).

Тогда .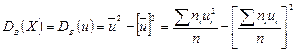

Замечание 3. Если первоначальные варианты являются десятичными дробями с k десятичными знаками после запятой, то, чтобы избежать действий с дробями, умножают первоначальные варианты на постоянное число 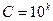, т.е. переходят к условным вариантам 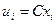. При этом дисперсия увеличится в 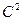раз. Поэтому, найдя дисперсию условных вариант, надо разделить ее на :

.

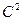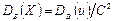Несмещенной оценкой генеральной дисперсии служит исправленная выборочная дисперсия

.

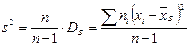Более удобна формула

.

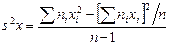В условных вариантах она имеет вид

,

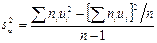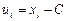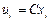причем если , то ; если , то .

Дата добавления: 2014-11-29