Прямое вычисление значений искажений

Алгоритм Берлекэмпа-Мэсси для исправления ошибок и стираний

• Итерация 0: Начальные установки.

• Итерация 1:

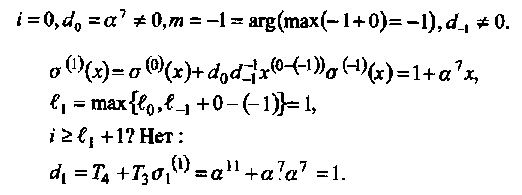
• Итерация 2:

• Итерация 3:

• Итерация 4

Таким образом, получаем многочлен локаторов ошибок

Напомним, что в последнем равенстве с помощью процедуры Ченя найдены обратные величины локаторов ошибок в поле GF(2^m). Действительно, проверка дает σ (а¹²) = 0 и о(а³) = 0. Следовательно, локаторами ошибок являются а^-12 = а³ иa^-3 = а¹².

Из определения (4.12) находим модифицированный многочлен значений искажений

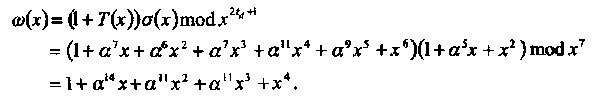(4.18)

Многочлен локаторов искажений равен

и, следовательно, ф'(х) = 1.

Значения ошибок и стираний могут быть вычислены по формулам (4.14) и (4.15), соответственно,

Отсюда следует, что многочлен искажений равен

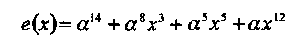
Результат декодирования v(x) = г(х) + е(х) совпадает с переданным словом v(x). Исправлены две ошибки и два стирания.

Для кодов PC с малым кодовым расстоянием значения стираний можно получить как решение системы линейных уравнений. Пусть е(х) полином ошибок, ассоциированный с комбинацией v ошибок и μ стираний,

(4.19)

Тогда справедлива следующая система линейных уравнений, аналогичная (4.8), связывающая синдромы и значения искажений:

(4.20)

где 1 ≤i≤ 2t_d. Как и раньше, может быть использовано любое подмножество v +μ≤t_d уравнений для определения значений всех стираний и ошибок.

Пример 44. Рассмотрим прямое вычисление значений искажений из предыдущего примера. После выполнения алгоритма Берлекэмпа-Мэсси и процедуры Ченя декодеру известны локаторы искажений и многочлен ошибок в виде

Значения искажений могут быть найдены из системы линейных уравнений (4.20), которая в матричной форме имеет

следующий вид

(4.21)

Легко проверить, что решением (4.21) являются f₀ = а¹⁴, е₃ = а⁸,f₅ = а⁵, e₁₂ = а. Эти значения совпадают со значениями искажений, вычисленными модифицированным алгоритмом Форни.

4.4. Распределение весов

Как упоминалось выше, коды PC являются МДР кодами. Распределение весов МДР кодов вычисляется точно с помощью следующего выражения [MS, LC]:

Число кодовых слов веса i МДР (n,k,d) кода над GF(q) равно

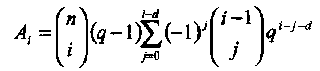(4.22)

Для оценки помехоустойчивости (n,k,d) PC кода над GF(q) можно использовать следующую границу (оценку сверху) вероятности ошибки на бит Р_b алгебраического декодера PC², которая легко вычисляется и дает достаточно хороший результат,

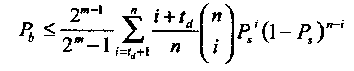(4.23)

где P_s вероятность ошибки на символ на входе декодера PC,

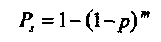
и р вероятность ошибки на бит на входе декодера. Вероятность ошибки на слово (включая неправильное декодирование и отказ от декодирования) ограничена сверху границей (1.31),

(4.24)

Вопросы для самоконтроля

1. Расскажите о работе алгоритма Мэсси по декодированию кода РС

2. Расскажите о работе алгоритма Евклида по декодированию кода РС

3. Опишите принципы работы алгоритма Берлекэмпа-Мэсси для исправления ошибок и стираний

4. Как рассчитывается распределение весов для РС кода

Дата добавления: 2014-11-29