Мощность множества

Лекция 3. Конечные и бесконечные множества.

Первым бесконечным множеством, с которым столкнулись люди было множество натуральных числел . И с давних времен было известно одно странное свойство множества .

Рассмотрим множество и множество всех четных чисел. Отображение , задаваемое функцией , является взаимнооднозначным. То есть каждому натуральному числу соответствует четное число, а каждому четному числу соответствует одно натуральное число. А это означает, что число элементов множества равно числу элементов множества . Но , более того, ясно, что содержит половину элементов . Это был парадокс. И объяснение ему нашлось значительно позже, после того, как Кантор ввел в математику понятие множества, и математики начали интенсивно изучать свойства множеств.

С парадоксом множества натуральных чисел математики справились решив, что бесконечные множества могут иметь свойства, отличающиеся от свойств конечных множеств. Например, часть может быть равна целому. Так же отнеслись к тому факту, что количества точек на двух отрезках разной длины равны.

Для доказательства этого нарисуем отрезки и разной длины на параллельных прямых. Точну пересечения прямых, проходящих через их концы, обозначим .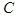

Теперь возьмем любую точку 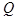на большем отрезке и найдем соответствующую ему точку 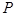на меньшем отрезке. Для этого достаточно соединить точк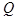и и 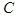отрезком. Точка 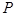на пересечении этого отрезка с отрезком и будет искомой. Легко видеть, что такая точка существует для каждой точки отрезка и является единственной.

Количество элементов в множестве стали называть его мощностью и обозначать знаком модуля. Например, . А чему равна мощность множества натуральных чмсел? То есть чему рано 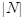? Она бесконечна, поэтому не равна никакому натуральному числу. Для обозначения мощности бесконечных множеств ввели специальные числа, которые стали называть трансцендентными. Ясно, что такие числа больше любого натурального числа. Обозначать такие числа решили первой буквой языка иврит, которая называется алеф и выглядит так 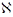. Так как таких чисел потребовалось много, то к букве стали добавлять индексы. Например, мощность множества натуральных чисел стали обозначать . Затем стали выяснять мощность других числовых множеств, и оказалось, что .

Докажем это. Для этого воспользуемся отображением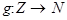

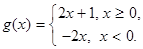
Это отображение ставит в соответствие каждому целому единственное натуральное число. При этом натуральные числа не повторяются, а значит их количество равно количеству целых чисел.

Можно показать также, что . Для этого нам понадобится функция , которая переводит множество пар натуральных чисел 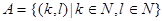в 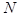. Эта функция выглядит следующим образом:

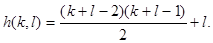
Действительно, она нумерует пары натуральных чисел “по диагонали”

Проверим для пары (3,2)

Построим теперь функцию Так как множество рациональных чисел опредеяется как

то можно считать, что это множество пар Но число целое, а мы умеем нумеровать с помощью функции 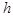только пары натуральных чисел. Значит надо сначала применить к функцию 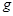, а потом к паре применить функцию Получится функция

Пример. Найти Решение.

Упражнение, Найти 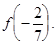Решение.

Наличие функции и доказывает, что .

Самостоятельная работа №3.

Дата добавления: 2014-11-28