Замечания о методе комплексных амплитуд

Будем рассматривать только линейные уравнения Максвелла (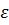, –постоянные). В этом случае при их решении может быть применён принцип суперпозиции (наложения), т. е. общее решение уравнений может быть представлено как сумма (или интеграл) частных решений.

Одним из математических приёмов, использующих этот принцип, является представление решения рядом или интегралом Фурье.

Как известно, при ограничениях, которые обычно соблюдаются в практических задачах радиотехники, периодическая функция может быть представлена в виде суммы простых гармонических слагаемых (ряд Фурье), а непериодическая – в виде интеграла от простой гармонической функции (интеграл Фурье).

Отсюда следует, что достаточно найти простое гармоническое решение системы уравнений, чтобы общее решение могло бы быть представлено в виде ряда или интеграла Фурье. Необходимо также определить входящие в общее решение произвольные постоянные (или функции) интегрирования так, чтобы полученное решение удовлетворяло не только уравнениям, но и начальным и граничным условиям.

Многие практические вопросы радиотехники с достаточной точностью позволяют воспользоваться решениями, полученными при самых простых предположениях. Так задачи об излучении и распространении радиоволн, источниками которых являются длительно работающие передатчики, генерирующие незатухающие колебания высокой частоты, решаются в предположении, что этот процесс чисто гармонический во времени, т. е. ограничиваются рассмотрением установившегося гармонического процесса. При этом отпадает ряд математических трудностей и, конечно, начальные условия.

Таким образом, рассмотрение частного чисто гармонического во времени решения уравнений Максвелла имеет исключительно важное значение как в теоретическом, так и в практическом отношении.

(1.82)

Гармонические функции при таком рассмотрении будут иметь вид:

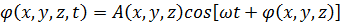
где 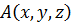– пространственная амплитуда;

– пространственная фаза;

– круговая частота;

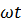– временная фаза;

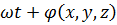– пространственно-временная фаза.

Функция (1.82) определяет величину, которая в любой точке пространства (фиксированные ) колеблется с течением времени по гармоническому закону. Однако амплитуды и фазы колебаний в различных точках пространства различны для данного момента времени.

Метод комплексных амплитуд заключается в том, что от истинных выражений для функции координат и времени переходим к комплексным изображениям. Этот метод позволяет избавиться от временной зависимости и перейти от тригонометрических функций к показательным:

.

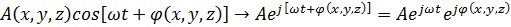Обозначим , которая называется комплексной амплитудой, тогда сама функция 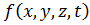определяется следующим образом:

Если возьмём частную производную от комплексного изображения по времени

то замечаем, что она равна самому комплексному изображению, умноженному на .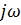

Пользуясь методом комплексных амплитуд, расчёты упрощаются. Для векторных функций можно пользоваться аналогичными преобразованиями.

Пусть вектор 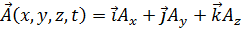и имеют место соотношения:

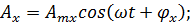
В этом случае данным функциям соответствуют следующие комплексные изображения:

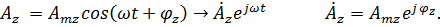
В этом случае

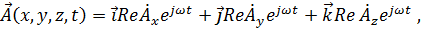
отсюда

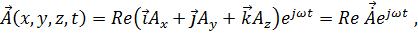
где 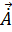– комплексная амплитуда вектора .

Следовательно,

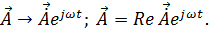
Метод комплексных амплитуд позволяет достаточно просто вычислить среднее значение произведений гармонических функций. Известно, например, что

Пусть

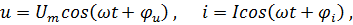
тогда

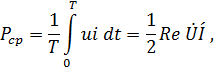
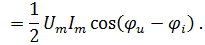где комплексно-сопряжённая амплитуда тока если ). Следовательно,

В теории электромагнитного поля доказывается, что

(1.83)

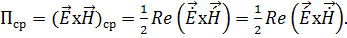
Выражение (1.83) есть среднее значение вектора Умова – Пойнтинга.

Дата добавления: 2014-11-28