
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Решение дифференциальных уравнений для линии без потерь
|
|
|
|
Для выяснения физической сущности решений дифференциальных уравнений (7.3) рассмотрим простейший случай, когда имеем идеальную длинную линию, т. е. линию без потерь [3,6]. В этом случае

и уравнения (7.3) примут вид:
|
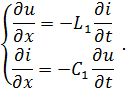
Для решения этой системы продифференцируем 1-е уравнение по координате 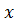 , а 2-е по времени
, а 2-е по времени 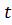 . Получим
. Получим
|

Из уравнений (7.5) имеем:
|
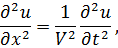
где 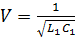 – имеет размерность скорости.
– имеет размерность скорости.
Если продифференцируем 1-е уравнение (7.4) по t, а 2-е уравнение по координате  , то получим уравнение для тока:
, то получим уравнение для тока:
|

Таким образом, получаем систему дифференциальных уравнений для напряжения и тока:
|

которые называются волновыми уравнениями или уравнениями Даламбера. Решения этих уравнений известны. Общее решение имеет вид:
|
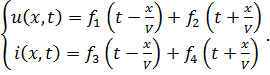
Функции  определяются конкретными условиями задачи (начальными условиями).
определяются конкретными условиями задачи (начальными условиями).
Решения (7.9) удовлетворяют уравнениям (7.8). В этом можно убедиться, если подставить эти решения в уравнения (7.8). Подставляя решения (7.9) в исходные уравнения (7.4), получим связь между функциями  :
:
|

Каков же физический смысл полученных решений? Рассмотрим для примера функцию  . Видим, что значения
. Видим, что значения  момент времени
момент времени 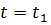 при различных значениях
при различных значениях  в общем случае будут различными. Но для двух различных значений
в общем случае будут различными. Но для двух различных значений  и
и  можно подобрать такие моменты наблюдения
можно подобрать такие моменты наблюдения  и
и 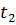 , при которых имеет место равенство
, при которых имеет место равенство

Это равенство выполняется в том случае, когда
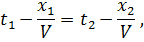
причём если  то и
то и  следовательно,
следовательно,
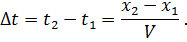
Отсюда видно, что значение функции  в точке
в точке  , при
, при  , повторяется в точке
, повторяется в точке  ,через промежуток времени
,через промежуток времени 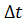 т. е. значения
т. е. значения 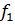 как бы движутся во времени вдоль оси
как бы движутся во времени вдоль оси 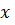 с постоянной скоростью:
с постоянной скоростью:
|
|
|
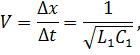
 |
определяемой погонными параметрами линии. Это свойство функции
 дает основание называть ее волновой функцией. На рис. 7.4 показано смещение функции
дает основание называть ее волновой функцией. На рис. 7.4 показано смещение функции  по оси
по оси 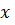 по времени
по времени  Вид этой функции взят произвольным.
Вид этой функции взят произвольным.
|
Таким образом, первые слагаемые в уравнениях (7.9) представляют волны напряжения и тока, распространяющиеся по линии вдоль оси 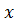 со скоростью
со скоростью  Эти волны называются прямыми (падающими) волнами.
Эти волны называются прямыми (падающими) волнами.
Аналогичные рассуждения показывают, что функции 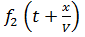 и
и 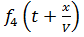 определяют волны, которые распространяются по линии в противоположном направлении. Эти волны называются обратными (отражёнными) волнами.
определяют волны, которые распространяются по линии в противоположном направлении. Эти волны называются обратными (отражёнными) волнами.
Таким образом, решения (7.9) можно записать в виде
|

При этом из уравнений (7.10) и (7.11) следует, что
|

где 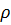 – волновое сопротивление линии.
– волновое сопротивление линии.
Волновое сопротивление – это сопротивление линии одному процессу либо падающему, либо отражённому. Так, например, для открытой двухпроводной линии

где значения  и
и  показаны на рис. 7.1а.
показаны на рис. 7.1а.
Мы получили решение для линии без потерь. В реальной линии с потерями также существуют две волны: прямая и обратная, но из-за наличия потерь их амплитуды будут затухать.
Таким образом, в общем случае в длинной линии существуют две волны: прямая (падающая) и обратная (отражённая).
|
|
|
|
|
Дата добавления: 2014-11-28; Просмотров: 886; Нарушение авторских прав?; Мы поможем в написании вашей работы!