КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Режимы работы длинной линии
|
|
|
|
Существуют следующие режимы работы длинной линии: режим бегущих волн, режим стоячих волн, режим смешанных волн. Наиболее общим является режим смешанных волн [3,4].
|

В этом случае коэффициент отражения

следовательно,
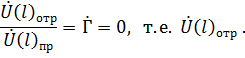
В данном случае отражённая волна отсутствует. Существует только падающая волна, которая переносит энергию от генератора к нагрузке.
Из (7.38) получим:
|

Но в соответствии с формулами (7.18) и (7.19) имеем

где  – начальная фаза.
– начальная фаза.
Выражения для  и
и  записаны в соответствии с методом комплексных амплитуд.
записаны в соответствии с методом комплексных амплитуд.
Положим, что начальные фазы 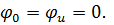 Найдём при этом условии мгновенные значения для напряжения и тока в длинной линии в случае режима бегущих волн:
Найдём при этом условии мгновенные значения для напряжения и тока в длинной линии в случае режима бегущих волн:
|

Если обозначить  , a
, a 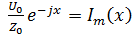 то выражения (7.44) примут вид:
то выражения (7.44) примут вид:
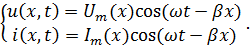
Падающие волны напряжения и тока распространяются от начала линии к концу (нагрузке) со скоростью 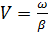
На рис. 7.7 приведены графики амплитуд напряжения и тока вдоль линии. Уменьшение амплитуд происходит по экспоненциальному закону вида  .
.
|
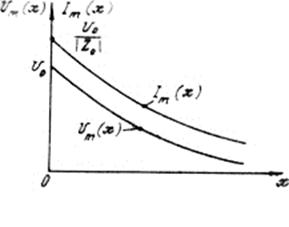
В случае же идеальной длинной линии или радиотехнического кабеля малой длины можно считать, что коэффициент затухания  достаточно мал, поэтому
достаточно мал, поэтому 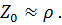 Тогда амплитуда напряжения и тока вдоль линии остаётся практически постоянной, как показано на рис. 7.8.
Тогда амплитуда напряжения и тока вдоль линии остаётся практически постоянной, как показано на рис. 7.8.
При передаче электромагнитной энергии с помощью длинной линии обычно стремятся к получению режима бегущих волн. Линия, в которой выполняется этот режим, называется фидером. В этом случае
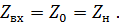
Для линии с малыми потерями ( ) в случае режима бегущих волн из (7.19) получаем:
) в случае режима бегущих волн из (7.19) получаем:
|
|
|
 (7.45)
(7.45)
т. е. сопротивление нагрузки чисто активное и равно волновому сопротивлению линии. Эквивалентная схема длинной линии для режима бегущих волн показана на рис. 7.9.

|
Из электротехники известно, что условием отдачи генератором максимальной мощности в линию является равенство сопротивлений нагрузки и внутреннего сопротивления генератора, а также их активный характер. Для данной линии это условие имеет вид:
|

|
 ,
,
где 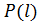 – мощность в нагрузке;
– мощность в нагрузке;
 – мощность на входе линии.
– мощность на входе линии.
Определим 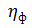 длинной линии. Для этого найдём мощности
длинной линии. Для этого найдём мощности 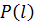 и
и  , используя метод комплексных амплитуд:
, используя метод комплексных амплитуд:

где 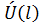 и
и 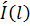 – комплексно сопряженные амплитуды напряжения и тока.
– комплексно сопряженные амплитуды напряжения и тока.
Запишем значения комплексных амплитуд:

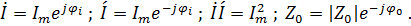
Учитывая эти равенства, получим:


Так как  , то
, то
|
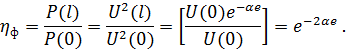
Когда 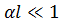 , что практически часто выполняется, раскладывая
, что практически часто выполняется, раскладывая  в ряд и пренебрегая членами второго порядка малости и выше, получаем приближённую формулу
в ряд и пренебрегая членами второго порядка малости и выше, получаем приближённую формулу

обычно  составляет 90 – 95 %.
составляет 90 – 95 %.
Режим стоячих волн имеет место, когда линия разомкнута, короткозамкнута или нагружена на чисто реактивное сопротивление. Заметим, что чистый режим стоячих волн имеет место только в идеальной длинной линии.
1. Рассмотрим разомкнутую линию (линию холостого режима).
В этом случае (рис. 7.10)  и коэффициент отражения
и коэффициент отражения
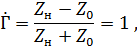
т. е. падающая волна полностью отражается от конца линии. В соответствии с (7.35)
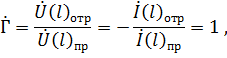
следовательно, фаза отражённой волны напряжения не изменяется при отражении, а фаза отражённой волны тока изменяется на  , так как
, так как 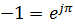 .
.
Таким образом, на конце линии напряжение и ток примут значения:
|

|
|
|
 |
т. е. напряжение на конце линии в два раза больше напряжения падающей волны (но не напряжения источника колебаний), ток же на конце линии равен нулю.
|
 следует
следует
|

Входное сопротивление в соответствии с формулой (7.40) при  определяется
определяется
|

Рассмотрим идеальную длинную линию, т. е.

В этом случае выражения (7.49) примут вид
|
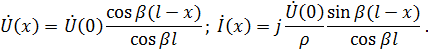
При этом использованы известные из математики соотношения
 ;
;  .
.
Для выяснения физической сущности полученных решений (7.51) запишем мгновенные значения для напряжения и тока, полагая, что 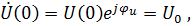 т. е.
т. е.  , тогда
, тогда
|
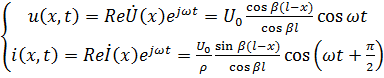 .
.
В выражениях (7.52) для напряжения и тока отсутствует множитель вида 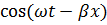 , характеризующий распространяющуюся волну, следовательно, процесс вдоль линии не распространяется.
, характеризующий распространяющуюся волну, следовательно, процесс вдоль линии не распространяется.
Амплитуды напряжения и тока изменяются в зависимости от координаты  пропорционально косинусу и синусу:
пропорционально косинусу и синусу:
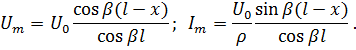
Колебания напряжения и тока сдвинуты во времени на 90°.
Графики напряжения и тока вдоль линии для некоторого момента времени показаны на рис. 7.11. (Здесь обозначено 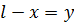 .) График изменения напряжения вдоль линии во времени приведён на рис. 7.12 (график для тока строится аналогично).
.) График изменения напряжения вдоль линии во времени приведён на рис. 7.12 (график для тока строится аналогично).
|

Перемещение волны не происходит, а напряжение и ток лишь изменяются во времени по гармоническому закону. Такой режим, когда нет перемещения волны (т. е. нет переноса энергии), называется режимом стоячих волн.
Сечения, которым соответствуют максимальные значения напряжения и тока, называются пучностями. Сечения, в которых значения напряжения и тока минимальны, называются узлами.
|

Следует отметить, что напряжение и ток в пучностях могут достигать большой величины, так как определяются они не только величиной  , но и знаменателем
, но и знаменателем 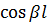 , который изменяется в пределах
, который изменяется в пределах  . Такую систему называют резонирующей.
. Такую систему называют резонирующей.
Средняя мощность, отдаваемая генератором в данном режиме,
|
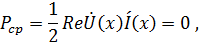
так как ток и напряжение сдвинуты по фазе на 90°. Это видно из выражений (7.51). Выражение для напряжения действительное, а для тока чисто мнимое, поэтому их реальная часть равна 0.
|
|
|
Определим входное сопротивление идеальной разомкнутой линии. Используя формулу (7.40)
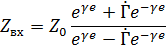
|
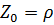 ;
; 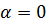 ,
, 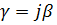 , получим:
, получим:

т. е. входное сопротивление разомкнутой линии носит чисто реактивный характер.
График зависимости входного сопротивления разомкнутой длинной линии от её длины приведён на рис. 7.13. Из графика следует, что на отдельных участках линия имеет либо индуктивное, либо ёмкостное сопротивления, которые эквивалентны сопротивлениям последовательного либо параллельного колебательного контура.
Вблизи точек, кратных  , линия ведёт себя как последовательный или параллельный колебательные контуры. Причём, если колебательный контур с сосредоточенными параметрами имеет только одну резонансную частоту
, линия ведёт себя как последовательный или параллельный колебательные контуры. Причём, если колебательный контур с сосредоточенными параметрами имеет только одну резонансную частоту 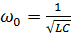 , то длинная линия имеет бесконечное множество резонансных частот. При изменении длины линии будут изменяться и резонансные частоты.
, то длинная линия имеет бесконечное множество резонансных частот. При изменении длины линии будут изменяться и резонансные частоты.

|
В сечениях, где линия эквивалентна последовательному колебательному контуру, должно выполняться условие 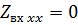 . Это условие будет выполняться при длине линии:
. Это условие будет выполняться при длине линии:

так как 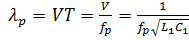 , то
, то
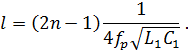
Отсюда находим частоту, при которой в линии возникает резонанс напряжений (как в последовательном колебательном контуре):
|

В точках, где линия эквивалентна параллельному колебательному контуру, должно выполняться условие 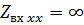 . Это условие будет выполняться при длине линии
. Это условие будет выполняться при длине линии  ,
, 
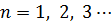 .
.
Рассуждая аналогично предыдущему случаю, получим  .
.
Отсюда находим частоту, при которой возникает резонанс токов (как в параллельном колебательном контуре):
|
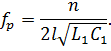
В реальной длинной линии вследствие наличия потерь ни напряжение, ни ток ни в одном сечении не обращаются в нуль, и на стоячую волну накладывается бегущая волна напряжения и тока, мощность которой расходуется на покрытие потерь в линии. В этом случае пучностям и узлам соответствуют лишь некоторые наибольшие и наименьшие значения напряжения и тока.
В реальной длинной линии с малыми потерями можно положить 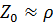 . Коэффициент же затухания
. Коэффициент же затухания  – величина конечная, отличная от нуля. Следовательно,
– величина конечная, отличная от нуля. Следовательно, 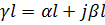 . Ввиду малости
. Ввиду малости  , справедливо, как правило, неравенство
, справедливо, как правило, неравенство 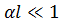 . Входное сопротивление реальной разомкнутой линии в этом случае будет комплексным, а не чисто реактивным:
. Входное сопротивление реальной разомкнутой линии в этом случае будет комплексным, а не чисто реактивным:
|
|
|
 .
.
 |
Зависимость
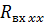 и
и  реальной разомкнутой линии с потерями от её длины имеет вид, показанный на рис. 7.14, где
реальной разомкнутой линии с потерями от её длины имеет вид, показанный на рис. 7.14, где
|

2. Рассмотрим короткозамкнутую линию (режим короткозамкнутой линии), которая представлена на рис. 7.15.
|
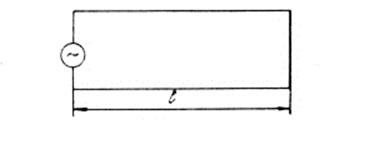
В этом случае  и коэффициент отражения
и коэффициент отражения

следовательно,

Отсюда следует, что амплитуда напряжения отражённой волны равна амплитуде падающей волны, а фаза отражённой волны меняется на  для тока
для тока
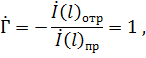
т. е. амплитуда отражённой волны тока также равна амплитуде падающей волны, причём отражённая волна тока своей фазы не изменяет. На конце линии напряжение и ток принимают следующие значения:
|

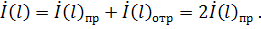
Найдём закон изменения напряжения и тока вдоль линии. В соответствии с формулами (7.38) имеем:
|

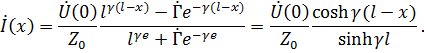
Рассмотрим случай идеальной линии, т. е. 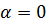 ,
, 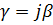 ,
, 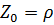
Положим, что начальные фазы  , тогда выражения для напряжения и тока (7.58) примут вид
, тогда выражения для напряжения и тока (7.58) примут вид

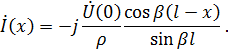
Переходя к мгновенным значениям, получим
|

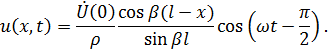
Отсюда следует, что в идеальной короткозамкнутой линии существует режим стоячих волн, так как отсутствует множитель вида 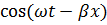 , характеризующий распространяющуюся волну.
, характеризующий распространяющуюся волну.
 |
На рис. 7.16 приведены графики изменения напряжения и тока вдоль линии, построенные в соответствии с формулами (7.59) для фиксированного момента времени. По оси абсцисс отложены значения
 . Максимальные значения напряжения и тока могут достигать большой величины, так как они определяются не только значением
. Максимальные значения напряжения и тока могут достигать большой величины, так как они определяются не только значением  , но и функцией
, но и функцией  , стоящей в знаменателе и имеющей пределы
, стоящей в знаменателе и имеющей пределы 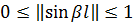 .
.
|
|
Найдём входное сопротивление идеальной короткозамкнутой линии. В соответствии с формулой (7.40) имеем:

Учитывая, что 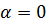 ;
; 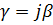 ;
; 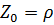 , a
, a  ,
,  , получим:
, получим:
|
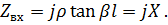
Отсюда видно, что входное сопротивление идеальной короткозамкнутой линии имеет чисто реактивный характер. На рис. 7.17 приведён график изменения входного сопротивления этой линии в зависимости от её длины.
|

Таким образом, входное сопротивление линии в зависимости от её длины может быть либо индуктивным, либо ёмкостным. В сечениях, соответствующих узлам или пучностям идеальной линии, её сопротивление эквивалентно сопротивлению либо параллельного, либо последовательного колебательных контуров при резонансе.
Из рис. 7.17 видно, что короткозамкнутая линия длиной 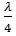 может применяться как металлический изолятор, так как её входное сопротивление в точках
может применяться как металлический изолятор, так как её входное сопротивление в точках 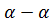 (рис. 7.18) на данной длине волны равно
(рис. 7.18) на данной длине волны равно 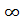 .
.
|

Рассуждая аналогично тому, как это сделано для разомкнутой линии, получим выражения для резонансных частот.
Если короткозамкнутая линия эквивалентна параллельному колебательному контуру в момент резонанса, то  . Это условие выполняется при длине линии
. Это условие выполняется при длине линии
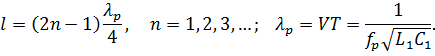
Следовательно,
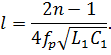
Отсюда найдём резонансные частоты:
|
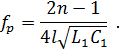
Если же короткозамкнутая линия эквивалентна последовательному контуру в момент резонанса, то  .
.
Это условие выполняется при длине линии
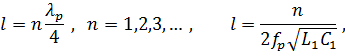
т. е. резонансные частоты:
|
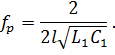
В реальной короткозамкнутой линии с малыми потерями равенство 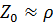 следует рассматривать как приближённое. Коэффициент затухания
следует рассматривать как приближённое. Коэффициент затухания  . Отсюда
. Отсюда 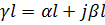 . Поэтому входное сопротивление будет не чисто реактивным, а комплексным:
. Поэтому входное сопротивление будет не чисто реактивным, а комплексным:
 .
.
Зависимость 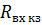 и
и  от длины линии показана на рис. 7.19, где
от длины линии показана на рис. 7.19, где
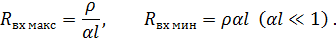
3. Рассмотрим линию, нагруженную на чисто реактивное сопротивление.
В этом случае  . Рассмотрим идеальную длинную линию. При этом коэффициент отражения имеет вид
. Рассмотрим идеальную длинную линию. При этом коэффициент отражения имеет вид
|
 ,
,
где 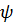 – фаза коэффициента отражения.
– фаза коэффициента отражения.
|

Вспомним, что для идеальной разомкнутой линии  , т. е.
, т. е.  , а для идеальной короткозамкнутой линии
, а для идеальной короткозамкнутой линии 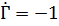 , т. е.
, т. е. 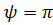 .
.
В случае же идеальной линии, нагруженной на чисто реактивную нагрузку  , а фаза
, а фаза  , причём
, причём  и
и  . Равенство
. Равенство  при чисто реактивной нагрузке говорит о том, что вместе включения линии будет режим стоячих волн. Отличие же фазы коэффициента отражения от
при чисто реактивной нагрузке говорит о том, что вместе включения линии будет режим стоячих волн. Отличие же фазы коэффициента отражения от  и
и  говорит о том, что в месте включения нагрузки не будет ни пучности, ни узла напряжения или тока.
говорит о том, что в месте включения нагрузки не будет ни пучности, ни узла напряжения или тока.
Пусть в качестве нагрузки включена индуктивность (рис. 7.20а). Индуктивность можно представить в виде эквивалентного отрезка длинной линии короткозамкнутой на конце длиной 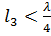 (рис. 7.206). Но для случая короткозамкнутой линии распределение амплитуд напряжения и тока вдоль линии нам уже известно (рис. 7.20в). Из последнего рисунка видно, что в случае чисто индуктивной нагрузки пучность напряжения находится ближе к нагрузке, чем узел, а узел тока ближе к нагрузке, чем пучность, причём эти расстояния меньше
(рис. 7.206). Но для случая короткозамкнутой линии распределение амплитуд напряжения и тока вдоль линии нам уже известно (рис. 7.20в). Из последнего рисунка видно, что в случае чисто индуктивной нагрузки пучность напряжения находится ближе к нагрузке, чем узел, а узел тока ближе к нагрузке, чем пучность, причём эти расстояния меньше  .
.
Пусть теперь в качестве нагрузки взята ёмкость (рис. 7.21а). Ёмкость можно представить в виде эквивалентного отрезка длинной линии короткозамкнутой на конце длиной 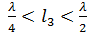 (рис. 7.21б).
(рис. 7.21б).
|

Для этого случая распределение амплитуд напряжения и тока вдоль линии нам уже известно (рис. 7.21в). Замечаем, что в случае чисто ёмкостной нагрузки узел напряжения находится ближе к нагрузке, чем пучность, а пучность тока находится ближе к нагрузке, чем узел.
|

Если будем измерять напряжение или ток в линии с помощью устройства, имеющего детектор, то получим распределение амплитуд напряжения и тока вдоль линии. Так для короткозамкнутой идеальной линии это распределение имеет вид (рис. 7.22). Аналогичным образом можно сделать построения и для других видов нагрузок.
|
|

Режим смешанных волн. При произвольной нагрузке существует как бегущая, так и стоячая волны. Такой режим называется режимом смешанных волн.
Рассмотрим случай идеальной длинной линии. Когда на конце линии нагрузка чисто активная, не равная волновому сопротивлению 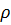 , или комплексная (рис. 7.23), то в линии существует режим смешанных волн.
, или комплексная (рис. 7.23), то в линии существует режим смешанных волн.
Найдём закон вменения напряжения и тока вдоль линии в этом случае. Так как линия идеальная, т. е. 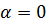 ,
, 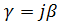 ,
, 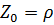 , то в соответствии с формулами (7.39) имеем
, то в соответствии с формулами (7.39) имеем
|

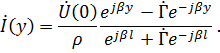
Определим модуль этих выражений. Для этого преобразуем их к виду:

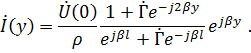
Пусть  , т. е. начальная фаза напряжения
, т. е. начальная фаза напряжения 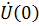 равна нулю, тогда
равна нулю, тогда 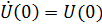 . Представим
. Представим 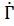 как комплексное число в показательной форме
как комплексное число в показательной форме 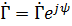 . Знаменатель в выражении (7.64) также запишем в показательной форме:
. Знаменатель в выражении (7.64) также запишем в показательной форме:

В результате получим


Нам же нужно определить модуль комплексных амплитуд напряжения и тока  и
и 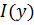 . Из преобразованных выражений следует, что
. Из преобразованных выражений следует, что
|


где 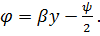
Проанализируем выражение (7.65). Для этого обозначим модули числителей
|
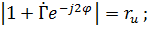
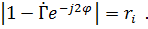
Из выражений (7.66) следует, что модули 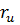 и
и 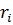 можно рассматривать: первый как сумму, а второй как разность двух векторов. Первый вектор – единичный, а второй вектор, модуль которого равен
можно рассматривать: первый как сумму, а второй как разность двух векторов. Первый вектор – единичный, а второй вектор, модуль которого равен  – вращающийся при изменении угла
– вращающийся при изменении угла  (рис. 7.24).
(рис. 7.24).
|
|
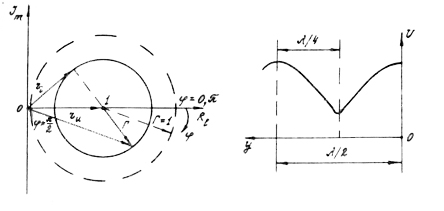
Причём следует отметить, что модуль коэффициента отражения  , поэтому на рисунке показана окружность для вполне определённого
, поэтому на рисунке показана окружность для вполне определённого  . При изменении угла
. При изменении угла  и
и  принимают максимальные и минимальные значения:
принимают максимальные и минимальные значения:
при  , а
, а 
при 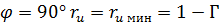 , а
, а 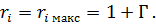
Когда коэффициент отражения  , то
, то  , a
, a  (на рис. 7.24 окружность
(на рис. 7.24 окружность  показана пунктиром), т. е. имеем режим стоячих волн.
показана пунктиром), т. е. имеем режим стоячих волн.
Когда  , то окружность вырождается в точку, при этом
, то окружность вырождается в точку, при этом  . Это соответствует режиму бегущих волн.
. Это соответствует режиму бегущих волн.
В других случаях будем иметь сечения с максимальными и минимальными значениями напряжения и тока. При этом сечению с максимумом напряжения соответствует минимум тока и наоборот.
Отношение
|
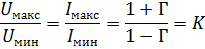
называется коэффициентом стоячей волны (КСВ). Это отношение имеет важное значение в радиотехнике. Из (7.67) следует, что КСВ изменяется в пределах 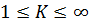 .
.
Иногда пользуются величиной, обратной КСВ, т. е.  , которая называется коэффициентом бегущей волны (КБВ). КБВ изменяется в пределах от
, которая называется коэффициентом бегущей волны (КБВ). КБВ изменяется в пределах от  до
до  , т. е.
, т. е. 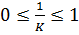 .
.
Изменение величины  при заданных нагрузках определяется изменением длины линии, т. е. координаты
при заданных нагрузках определяется изменением длины линии, т. е. координаты 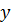 . Используя это положение, можно определить, на каком расстоянии друг от друга находятся максимумы и минимумы или те и другие в отдельности (рис. 7.25).
. Используя это положение, можно определить, на каком расстоянии друг от друга находятся максимумы и минимумы или те и другие в отдельности (рис. 7.25).
Известно, что
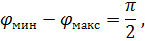
т. е. 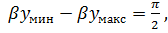
следовательно, 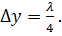
Рассмотрим некоторые частные случаи.
1. Нагрузка чисто активная 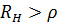 . В этом случае
. В этом случае 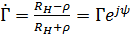 ;
;  , причём
, причём 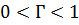 . Так как
. Так как  , то из формулы
, то из формулы 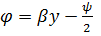 имеем
имеем  . На конце линии, т. е. при
. На конце линии, т. е. при  и
и 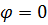 . Но при
. Но при 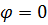 ,
, 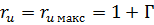 (см. рис. 7.24). Так как имеем
(см. рис. 7.24). Так как имеем  , то и на конце линии, т. е. на нагрузке, как следует из (7.65), будем иметь максимум напряжения
, то и на конце линии, т. е. на нагрузке, как следует из (7.65), будем иметь максимум напряжения  , а ток будет минимален
, а ток будет минимален  , так как
, так как 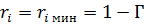 (рис. 7.26а).
(рис. 7.26а).
|

2. Нагрузка чисто активная  . В этом случае коэффициент отражения
. В этом случае коэффициент отражения
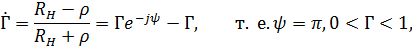
следовательно, 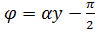 . На конце линии при
. На конце линии при  ,
,  .
.
На рис. 7.24 показано, что в этом случае  , а
, а 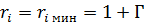 . Отсюда следует, что на конце линии, т. е. на нагрузке, будет минимум напряжения
. Отсюда следует, что на конце линии, т. е. на нагрузке, будет минимум напряжения  и максимум тока
и максимум тока  (рис. 7.266).
(рис. 7.266).
3. Нагрузка комплексная  . В этом случае модуль коэффициента отражения также изменяется в пределах
. В этом случае модуль коэффициента отражения также изменяется в пределах 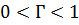 :
:
а) если нагрузка индуктивного характера  , то
, то 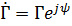 ,
,  . Анализ формул (7.65) и
. Анализ формул (7.65) и  показывает, что в этом случае ближе к нагрузке будет находиться максимум напряжения и минимум тока (рис. 7.27а);
показывает, что в этом случае ближе к нагрузке будет находиться максимум напряжения и минимум тока (рис. 7.27а);
б) если нагрузка ёмкостного характера  , то
, то 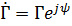 ,
, 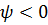 ,
, 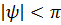 . Анализ тех же формул (7.65) и
. Анализ тех же формул (7.65) и  показывает, что в этом случае ближе к нагрузке будет находиться максимум тока и минимум напряжения (рис. 7.27б).
показывает, что в этом случае ближе к нагрузке будет находиться максимум тока и минимум напряжения (рис. 7.27б).
|
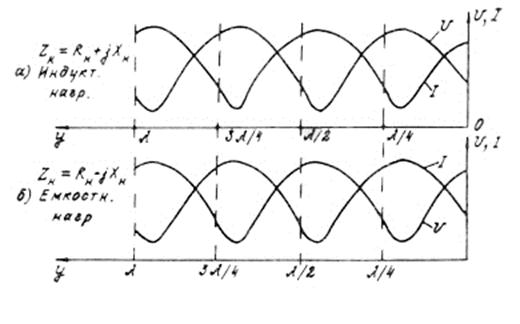
В рассмотренных случаях в линии будут иметь место максимумы и минимумы напряжения и тока, что является отличительным признаком режима смешанных волн в отличие от узлов и пучностей в случае режима стоячих волн.
|
|
|
|
|
Дата добавления: 2014-11-28; Просмотров: 11013; Нарушение авторских прав?; Мы поможем в написании вашей работы!