Градиент

Как мы видели, скалярное и векторное поля определяются соответственно скалярной и векторной функциями векторного аргумента (радиус-вектора). Возникает вопрос об установлении правил дифференцирования по векторному аргументу. Не входя в детали, эти правила легко устанавливаются, если будем основываться на аналитическом представлении скалярной и векторной функций в декартовой прямоугольной системе координат.

Рассмотрим поле скалярной функции φ(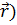, аналитическое представление которой есть φ(x, y, z). Очевидно, приращение dφ функции φ при переходе от точки M(x, y, z) в точку M’(x+dx, y+dy, z+dz) будет

Но dx, dy и dz – компоненты приращения радиус a-вектора

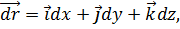
проведённого от точки M(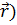 к точке M’(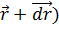. Введём в рассмотрение некоторый вектор, называемый градиентом функции φ,

Этот вектор имеет составляющими по осям декартовой системы координат частные производные

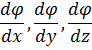
и численно равен

Тогда выражение для dφ приобретает вид

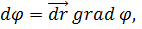(7)

остающийся неизменным в любой системе координат в соответствии с определением понятия векторов и их скалярного произведения.

Если точк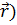и M( и M’(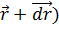 выбраны на прямой l, имеющей определенное направление, отмечаемое единичным вектором , то, очевидно, 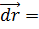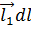и, следовательно,

Отсюда получаем важное понятие о производной скалярной функции φ по направлению

(8)

Соотношение (7) весьма характерно для градиента; из него следует, что если для какого-либо вектора 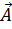имеет место соотношение 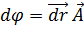, то .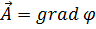

Из выражения (8) следует, что градиент φ является вектором, имеющим направление быстрейшего увеличения φ и по величине равным производной от φ по этому направлению.

Так как на поверхности уровня φ=const, то производная по любому направлению , лежащему в касательной плоскости к поверхности уровня в точке М, равна нулю. Следовательно, для любого такого направления из выражения (8) вытекает .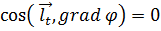

Таким образом, перпендикулярен к поверхности уровня в точке М и направлен в ту сторону нормали, куда φ возрастает.

Вектор, являющийся градиентом скаляра φ, называется потенциальным вектором, а поле такого вектора – потенциальным.

Для потенциального вектора имеет место такая важная теорема: линейный интеграл вектора вдоль какой-либо кривой l, соединяющей точки М₀( и М₁(, равен разности значений функции в точках М₁ и М₀.

Действительно,

Отсюда непосредственно следует, что если функция φ однозначна, то значение линейного интеграла не зависит от пути интегрирования, а только от конечных точек пути. Следовательно, интеграл градиента однозначной функции φ по замкнутому контуру (циркуляция градиента) равен нулю, так как конечные точки пути совпадают.

Последнее свойство характерно для потенциального вектора, так как справедлива и обратная теорема: если линейный интеграл вектора 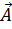вдоль всякой замкнутой кривой равен нулю, то вектор 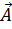есть градиент некоторого скаляра φ.

Если функция φ многозначна, то теорема о независимости линейного интеграла от пути интегрирования и, следовательно, теорема о циркуляции остаются справедливыми лишь после того, как многосвязная область, занятая полем функции φ, превращена в односвязную введением соответствующих дополнительных границ, пересечение которых кривой интегрирования запрещается.

Аналогично предыдущему можно определить производную вектора 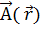по направлению .

Для составляющих вектора d 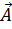имеем

и так далее.

Умножив на соответствующие орты ( и сложив, получаем

(9)

По аналогии с формулой (7), которая может быть записана в виде

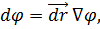
уместно положить

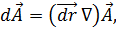
где использован символический дифференциальный оператор Гамильтона «набла»

Полагая 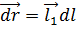, где, как и ранее, – единичный вектор, указывающий направление отрезка 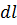, получаем выражение производной вектора по направлению

Такое представление производной вектора по направлению позволяет ввести несколько более общую операцию, называемую градиентом вектора 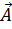по вектору 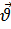и обозначаемую символом

(10)

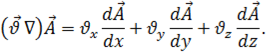
Производная вектора по вектору находит применение при рассмотрении полей, связанных с подвижной средой, а также в формулах преобразований. В случае подвижной среды координаты точек среды, с которыми сопоставляется поле скаляра или вектора, являются функциями времени. Тогда, если 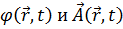, то

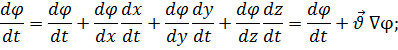
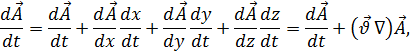
где

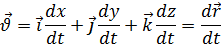
– скорость движения среды.

Дата добавления: 2014-11-28