
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Вычисление интегралов. Замена переменных
|
|
|
|
Вычислить заданный интеграл непосредственным интегрированием
удаётся не всегда. Одним из наиболее эффективных приёмов
является метод подстановки или замены переменной интегрирования.
Сущность этого метода заключается в том, что путём введения новой переменной интегрирования удаётся свести заданный интеграл к
новому интегралу, который берётся непосредственным интегрированием.
Рассмотрим этот метод:
Пусть 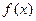 - непрерывная функция
- непрерывная функция
необходимо найти:  (1)
(1)
Сделаем замену переменной интегрирования:
х = φ (t) (2)
где φ (t) – монотонная функция, которая имеет непрерывную производную
и существует сложная функция f (φ (t)).
Применив к F (х) = F(φ (t)) формулу дифференцирования сложной
функции, получим:
﴾F (φ (t))﴿′ = F′(x) ∙ φ′ (t)
Но F′(x) = f (x) = f (φ (t)), поэтому
﴾F (φ (t))﴿′ = f (φ (t)) ∙ φ′ (t) (3)
Таким образом, функция F(φ (t)) является первообразной для функции
f (φ (t)) ∙ φ′ (t), поэтому:
∫ f (φ (t)) ∙ φ′ (t) dt = F (φ (t)) + C (4)
Учитывая, что F (φ (t)﴿ = F (x), из (1) и (4) следует формула замены
переменной в неопределённом интеграле:
∫ f (x)dx = ∫ f(φ (t)) φ′ (t)dt (5)
Формально формула (5) получается заменой х на φ (t) и dх на φ′ (t)dt
В полученном после интегрирования по формуле (5) результате следует
перейти снова к переменной х. Это всегда возможно, так как по предпо-
ложению функция х = φ (t) монотонна.
Удачный выбор подстановки обычно представляет известные труд-
ности. Для их преодоления необходимо овладеть техникой дифферен-
цирования и хорошо знать табличные интегралы.
Но все же можно установить ряд общих правил и некоторых приемов
|
|
|
интегрирования.
Правила интегрирования способом подстановки:
1. Определяют, к какому табличному интегралу приводится данный интеграл (предварительно преобразовав подинтегральное выражение, если нужно).
2. Определяют, какую часть подинтегральной функции нужно заменить
новой переменной, и записывают эту замену.
3. Находят дифференциалы обеих частей записи и выражают дифферен-
циал старой переменной (или выражение, содержащее этот диффе-
ренциал) через дифференциал новой переменной.
4. Производят замену под интегралом.
5. Находят полученный интеграл.
6. В результате переходят к старой переменной.
Примеры решения интегралов способом подстановки:
1. Найти: ∫ х²(3+2х  )
)  dx
dx
Решение:
сделаем подстановку 3+2х  = t
= t
Найдём дифференциал обеих частей подстановки:
6x 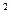 dx = dt, откуда
dx = dt, откуда
х²dx =  dt.
dt.
Следовательно:
∫ x 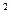 (3+2x
(3+2x  )
)  dx = ∫ t
dx = ∫ t  ∙
∙  dt =
dt =  ∫ t
∫ t  dt =
dt =  ∙
∙ 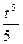 + C =
+ C = 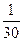 t
t 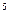 + C
+ C
Заменив t на его выражение из подстановки, получим:
∫ x 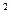 (3+2x
(3+2x  )
)  dx =
dx = 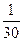 (3+2x
(3+2x  )
) 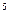 + С
+ С
2. Найти: 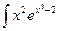
Решение:
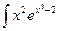 =
=  =
=  ∫ е
∫ е 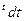 =
=  е
е  + C =
+ C =  е
е  + C
+ C
3. Найти: 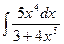
Решение:
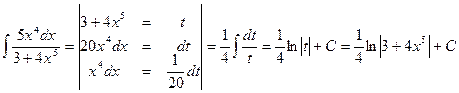
4. Найти 
Решение:
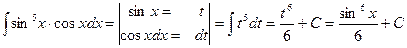
5. Найти: 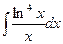
Решение:

6. Найти: 
Решение:

Рекомендации по выполнению третьего задания
домашней контрольной работы по теме
«Вычисление площадей плоских фигур и объёмов тел вращения с помощью определённого интеграла»
Понятие определённого интеграла.
Разность значений  для любой первообразной функции
для любой первообразной функции  при изменении аргумента от
при изменении аргумента от 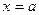 до
до  называется определенный интегралом этой функции в пределах от а до b и обозначается:
называется определенный интегралом этой функции в пределах от а до b и обозначается:
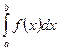
а и b называются нижним и верхним пределами интегрирования.
Чтобы вычислить определенный интеграл 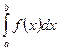 нужно:
нужно:
1. Найти соответствующий неопределенный интеграл 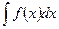
2. Подставить в полученное выражение вместо х сначала верхний предел интегрирования в, а затем нижний – а.
|
|
|
3. Из первого результата подстановки вычесть второй.
Коротко это правило записывается в виде формул так:
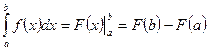

Эта формула называется формулой Ньютона - Лейбница.
Основные свойства определенного интеграла:
1.  , где K=const
, где K=const
2. 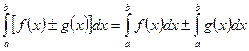
3. Если  , то
, то 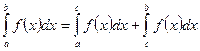
4. Если функция  неотрицательна на отрезке
неотрицательна на отрезке  , где
, где 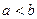 , то
, то 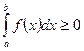
5. 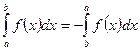
При замене в определенном интеграле старой переменной интегрирования на новую необходимо старые пределы интегрирования заменить новыми. Эти новые пределы определяются выбранной подстановкой.
Применение определённого интеграла.
Площадь криволинейной трапеции ограниченной кривой  , осью абсцисс и двумя прямыми
, осью абсцисс и двумя прямыми 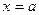 и
и  вычисляется по формуле:
вычисляется по формуле:
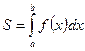
Объем тела, образованного вращением вокруг оси абсцисс криволинейной трапеции, ограниченной кривой  , не меняющей свой знак на
, не меняющей свой знак на  , осью абсцисс и двумя прямыми
, осью абсцисс и двумя прямыми 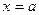 и
и  вычисляется по формуле:
вычисляется по формуле:

С помощью определенного интеграла можно решать и ряд физических задач.
Например:
--Если скорость прямолинейно движущегося тела 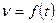 является известной функцией времени t, то путь S, пройденный этим телом с момента времени t = t1 до момента времени t = t2 определяется формулой:
является известной функцией времени t, то путь S, пройденный этим телом с момента времени t = t1 до момента времени t = t2 определяется формулой:
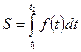
--Если переменная сила  является известной функцией пути S (при этом предполагается, что направление силы не меняется) то работа А, совершаемая этой силой на пути от
является известной функцией пути S (при этом предполагается, что направление силы не меняется) то работа А, совершаемая этой силой на пути от 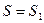 до
до 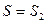 определяется формулой:
определяется формулой: 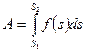
Примеры:
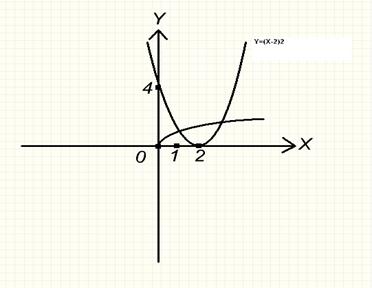
1. Вычислить площадь фигуры, ограниченной линиями:
y = 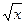
 ; y = (x-2)2; 0x.
; y = (x-2)2; 0x. 
Решение:
а) Построим графики функций: y = 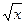
 ; y = (x-2)2
; y = (x-2)2
б) Определим фигуру, площадь которой нужно вычислить.
в) Определим пределы интегрирования, решая уравнение: 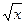 = (x-2)2; x = 1;
= (x-2)2; x = 1;
г) Вычисляем площадь заданной фигуры:
S =  dx +
dx + 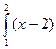 2 dx = 1 ед2
2 dx = 1 ед2
2. Вычислить площадь фигуры, ограниченной линиями:
Y = x2; x = y2.
Решение:
x 2 = 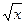 ; x 4 = x;
; x 4 = x;
x (x 3 – 1) = 0
x1 = 0; x2 = 1

S = 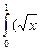 - x2) dx = (
- x2) dx = ( x3\2 -
x3\2 - 
 ) │01 =
) │01 = 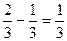 ед2
ед2
3. Вычислить объём тела, полученного вращением вокруг оси 0x фигуры, ограниченной линиями: y = 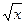 ; x = 1.
; x = 1.
Решение:
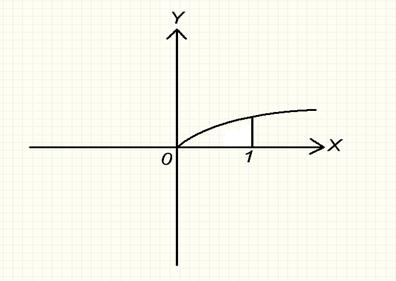
V = π  dx = π
dx = π 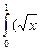 )2 dx =
)2 dx =  π
π 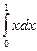 = π
= π  │
│ 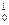 = π/2 ед.3
= π/2 ед.3
Домашняя контрольная работа по математике
Варианты заданий.
Вариант №1
1. Решить систему уравнений тремя способами:
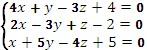
|
|
|
2. Вычислить интегралы заменой переменной:
1. 
2. 
3. 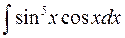
4. 
5. 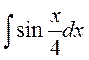
3. Вычислить площадь фигуры, ограниченной линиями:
y = (x + 1)2 ; y = 1 – x; 0x
Вариант № 2
1. Решить систему уравнений тремя способами:
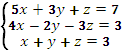
2. Вычислить интегралы заменой переменной:
1. 
2. 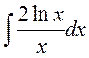
3. 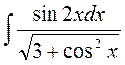
4. 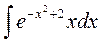
5. 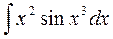

3. Вычислить площадь фигуры, ограниченной линиями:
y = 6 – x; y = x2 + 4
Вариант №3.
1. Решить систему уравнений тремя способами:

2. Вычислить интегралы заменой переменной:
1. 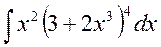
2. 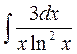
3. 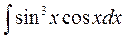
4. 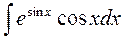
5. 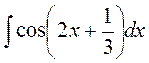
3. Вычислить площадь фигуры, ограниченной линиями:
y = - x2 + 5; y = x + 3
Вариант №4.
1. Решить систему уравнений тремя способами:

2. Вычислить интегралы заменой переменной:
1. 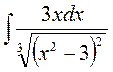
2. 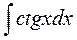
3. 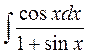
4. 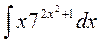
5. 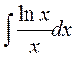
3. Вычислить площадь фигуры, ограниченной линиями:
y = x2; x = 3; Ox
Вариант №5.
1. Решить систему уравнений тремя способами:
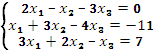
2. Вычислить интегралы заменой переменной:
1. 
2. 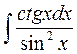
3. 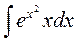
4. 
5. 
3. Вычислить площадь фигуры, ограниченной линиями:
y = 3 + 2x – x2; Ox
Вариант №6.
1. Решить систему уравнений тремя способами:
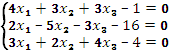
2. Вычислить интегралы заменой переменной:
1. 
2. 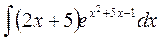
3. 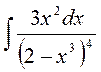
4. 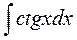
5. 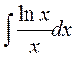
3. Вычислить площадь фигуры, ограниченной линиями:
y = x + 6 ; y = 8 + 2x – x2
Вариант № 7
1. Решить систему уравнений тремя способами:

2. Вычислить интегралы заменой переменной:
1. 
2. 
3. 
4. 
5. 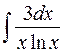
3. Вычислить объём тела, образованного вращением вокруг Ox фигуры ограниченной линиями:
y = sin x; y = 0; x = 0; x = π
Вариант №8.
1. Решить систему уравнений тремя способами:
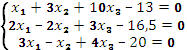
2. Вычислить интегралы заменой переменной:
1. 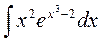
2. 
3. 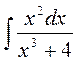
4. 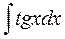
5. 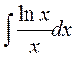
3. Вычислить площадь фигуры, ограниченной линиями:
y = 4 - x2 ; y = (x – 2)2; Ox
Вариант №9.
1. Решить систему уравнений тремя способами:

2. Вычислить интегралы заменой переменной:
1. 
2. 
|
|
|
3. 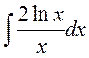
4. 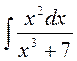
5. 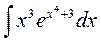
3. Вычислить площадь фигуры, ограниченной линиями:
y = - x2 - 1 ; y = 0; x = - 1; x = 2;
Вариант №10.
1. Решить систему уравнений тремя способами:
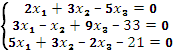
2. Вычислить интегралы заменой переменной:
1. 
2. 
3. 
4. 
5. 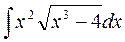
3. Вычислить площадь фигуры, ограниченной линиями:
y = 5 – x; y = __ x + 2; Ox
2
Вариант №11.
1. Решить систему уравнений тремя способами:

2. Вычислить интегралы заменой переменной:
1. 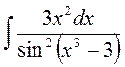
2. 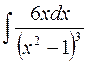
3. 
4. 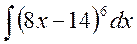
5. 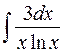
3. Вычислить объём тела, образованного вращением вокруг Ox фигуры ограниченной линиями:
y = x2 - 4; y = 0
Вариант №12.
1. Решить систему уравнений тремя способами:
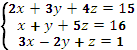
2. Вычислить интегралы заменой переменной:
1. 
2. 
3. 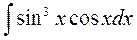
4. 
5. 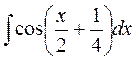
3. Вычислить площадь фигуры, ограниченной линиями:
y = (x + 1)2 ; y = 0; x = 0
Вариант №13.
1. Решить систему уравнений тремя способами:
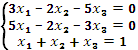
2. Вычислить интегралы заменой переменной:
1. 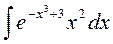
2. 
3. 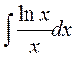
4. 
5. 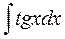
3. Вычислить площадь фигуры, ограниченной линиями:
y = x3 ; x = 0; y = 1
Вариант №14.
1. Решить систему уравнений тремя способами:
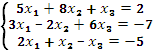
2. Вычислить интегралы заменой переменной:
1. 
2. 
3. 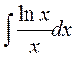
4. 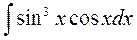
5. 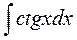
3. Вычислить площадь фигуры, ограниченной линиями:
y = x2 + 1 ; y = 0; x = 0; x = 1
Вариант №15.
1. Решить систему уравнений тремя способами:

2. Вычислить интегралы заменой переменной:
1. 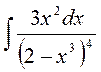
2. 
3. 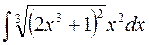
4. 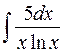
5. 

3. Вычислить объём тела, образованного вращением вокруг Ox фигуры ограниченной линиями:
y2 = 4x; y = x;
Список литературы
1. Письменный Д.Т. Конспект лекций по высшей математике Части 1, 2. М. АЙРИС ПРЕСС, 2006г.
2. Григорьев В.П., Дубинский Ю.А. Элементы высшей математики. М. Академия, 2008г.
3. Выгодский М.Я. Справочник по высшей математике. М. Наука,2001г.
4. Шипачев В.С. Высшая математика. М. Высшая школа,2005г.
5. Шипачев В.С. Задачник по высшей математике. М. Высшая школа,2005г.
|
|
|
|
|
Дата добавления: 2014-11-29; Просмотров: 1817; Нарушение авторских прав?; Мы поможем в написании вашей работы!