
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Цепь переменного тока с активным сопротивлением и индуктивностью
|
|
|
|
Рис.2.21 изображает неразветвлённую цепь с активным сопротивлением R и индуктивностью L.
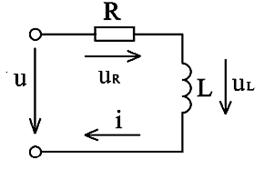
Рис.2.21. Цепь переменного тока с активным сопротивлением и индуктивностью
Пусть мгновенный ток в цепи изменяется по закону  . Тогда мгновенное напряжение на активном сопротивлении
. Тогда мгновенное напряжение на активном сопротивлении 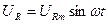 , так как на этом участке напряжение и ток совпадают по фазе. Напряжение на катушке индуктивности
, так как на этом участке напряжение и ток совпадают по фазе. Напряжение на катушке индуктивности  , поскольку на индуктивности напряжение опережает по фазе ток на угол
, поскольку на индуктивности напряжение опережает по фазе ток на угол 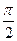 .
.
Построим для действующих значений напряжения и тока векторную диаграмму для рассматриваемой цепи (рис. 2.22).
Векторы 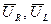 и
и 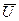 образуют треугольник напряжений. Выведем закон Ома для этой цепи. Из треугольника напряжений имеем
образуют треугольник напряжений. Выведем закон Ома для этой цепи. Из треугольника напряжений имеем 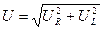 . Но
. Но  , а
, а 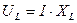 , где
, где 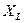 - индуктивное сопротивление, следовательно:
- индуктивное сопротивление, следовательно:
 , откуда
, откуда
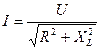 . (2.22)
. (2.22)
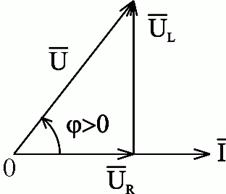
Рис.2.22. Векторная диаграмма действующих значений тока и напряжения цепи переменного тока с активным сопротивлением и индуктивностью
Введем обозначение 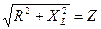 , где Z - полное сопротивление цепи. Тогда выражение закона Ома примет вид:
, где Z - полное сопротивление цепи. Тогда выражение закона Ома примет вид:
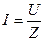 . (2.23)
. (2.23)
Полное сопротивление Z можно определить из треугольника сопротивлений (рис. 2.23).
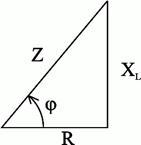
Рис.2.23. Треугольник сопротивлений цепи переменного тока с активным сопротивлением и индуктивностью
Сдвиг фаз  между током и напряжением определяется из треугольника сопротивлений:
между током и напряжением определяется из треугольника сопротивлений:
 , (2.24)
, (2.24)
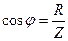 . (2.25)
. (2.25)
Поскольку вектор 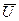 сдвинут по фазе относительно вектора
сдвинут по фазе относительно вектора  на угол
на угол  против часовой стрелки, этот угол имеет положительное значение.
против часовой стрелки, этот угол имеет положительное значение.
Если 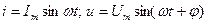 , то мгновенная мощность
, то мгновенная мощность  . Для действующих значений произведение
. Для действующих значений произведение 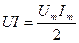 , откуда
, откуда  . Выражение
. Выражение  . Исходя из этого,
. Исходя из этого,
 . (2.26)
. (2.26)
Таким образом, мгновенная мощность переменного тока может быть представлена в виде постоянной величины  и, изменяющейся около неё с двойной частотой, величины
и, изменяющейся около неё с двойной частотой, величины  (рис. 2.24).
(рис. 2.24).
|
|
|
Введем понятие средней или активной мощности:
 . (2.27)
. (2.27)
Активная мощность характеризует расход энергии на активном сопротивлении.
Реактивная мощность характеризует обмен энергий между индуктивной катушкой и источником:
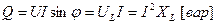 . (2.28)
. (2.28)
Полная мощность оценивает предельную мощность нагрузки:
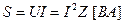 . (2.29)
. (2.29)
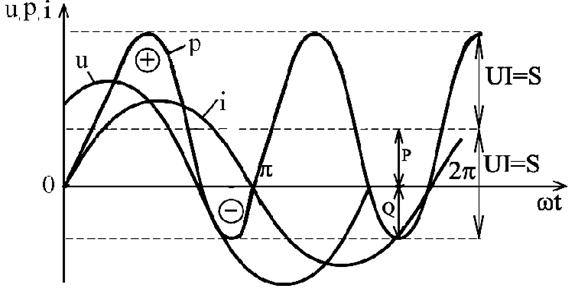
Рис.2.24. Зависимости мгновенных значений напряжения, тока и мощности цепи переменного тока с активным сопротивлением и индуктивностью
Совокупность всех мощностей можно определить из треугольника мощностей (рис. 2.25).
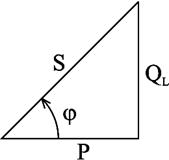
Рис.2.25. Треугольник мощностей
Так: 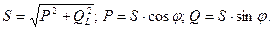 Обозначим коэффициент мощности в виде соотношения
Обозначим коэффициент мощности в виде соотношения 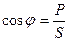 .
.
Коэффициент мощности cosφ изменяется от 0 до 1. По его величине судят, какую часть полной мощности составляет активная мощность. На практике стремятся к увеличению cosφ.
2.7. Цепь переменного тока с активным сопротивлением и ёмкостью
Рассмотрим электрическую схему цепи с активным сопротивлением и ёмкостью (рис. 2.26).
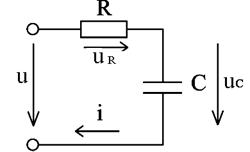
Рис.2.26. Цепь переменного тока с активным сопротивлением и ёмкостью
Зададимся током  , тогда
, тогда 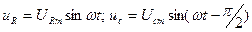 . На основании приведенных выражений построим векторную диаграмму цепи (рис.2.27) для действующих значений напряжений
. На основании приведенных выражений построим векторную диаграмму цепи (рис.2.27) для действующих значений напряжений  .
.

Рис.2.27. Векторная диаграмма действующих значений тока и напряжения цепи переменного тока с активным сопротивлением и ёмкостью
Из векторной диаграммы следует, что  . Но
. Но 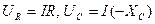 , где
, где  - емкостное сопротивление. Таким образом,
- емкостное сопротивление. Таким образом, 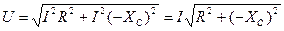 , откуда:
, откуда:
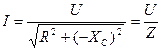 . (2.30)
. (2.30)
На рис. 2.28 изображен треугольник сопротивлений. Сдвиг фаз (угол  ) в этом случае отрицателен, так как напряжение отстает по фазе от тока:
) в этом случае отрицателен, так как напряжение отстает по фазе от тока:
 . (2.31)
. (2.31)
Пусть 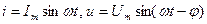 , тогда мгновенная мощность в цепи с R и C будет:
, тогда мгновенная мощность в цепи с R и C будет:  . Опустив промежуточные преобразования, получим:
. Опустив промежуточные преобразования, получим:
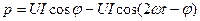 . (2.32)
. (2.32)
Средняя или активная мощность определяется постоянной составляющей мгновенной мощности: 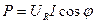 .
.
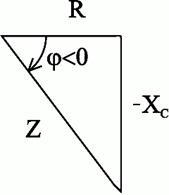
Рис.2.28. Треугольник сопротивлений цепи переменного тока с активным сопротивлением и ёмкостью
|
|
|
Реактивная емкостная мощность характеризует интенсивность обмена энергий между источником и ёмкостью: 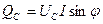 . Так как
. Так как  < 0, то реактивная мощность
< 0, то реактивная мощность 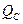 < 0. Полная мощность определяется из треугольника мощностей (рис. 2.29):
< 0. Полная мощность определяется из треугольника мощностей (рис. 2.29): 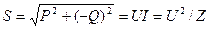 .
.

Рис.2.29. Треугольник мощностей
2.8. Неразветвлённая цепь переменного тока с активным сопротивлением, индуктивностью и ёмкостью. Резонанс напряжений
Рассмотрим неразветвлённую электрическую цепь (рис. 2.30).
Пусть  , тогда
, тогда 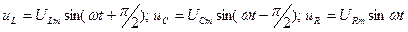 .
.
Построим векторную диаграмму при условии, что действующие значения напряжений 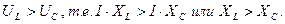
Из векторной диаграммы (рис.2.31) следует:  , откуда
, откуда 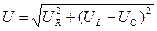 . Но
. Но 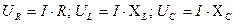 , следовательно
, следовательно  .
.

Рис.2.30. Схема неразветвлённой электрической цепи с активным сопротивлением, индуктивностью и ёмкостью
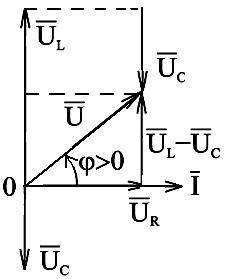
Рис.2.31. Векторная диаграмма действующих значений тока и напряжений для цепи переменного тока с активным сопротивлением, индуктивностью и ёмкостью, в которой ( )
)
Введя обозначение полного сопротивления цепи 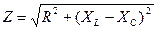 , найдем:
, найдем:
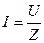 . (2.33)
. (2.33)
Разность между индуктивным и емкостным сопротивлениями называют реактивным сопротивлением цепи X = XL - XC. Учитывая это, получим треугольник сопротивлений для цепи с R, L и C (рис. 2.32).
При XL > XC реактивное сопротивление положительно и угол  > 0.
> 0.
Аналогично можно построить векторную диаграмму для действующих значений напряжений 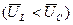 (рис. 2.33) и треугольник сопротивлений
(рис. 2.33) и треугольник сопротивлений  (рис. 2.34).
(рис. 2.34).

Рис.2.32. Треугольник сопротивлений цепи переменного тока с активным сопротивлением, индуктивностью и ёмкостью (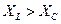 )
)
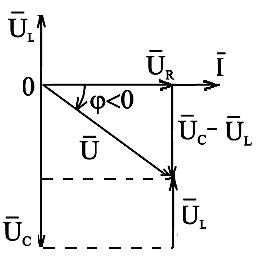
Рис.2.33. Векторная диаграмма действующих значений тока и напряжений
(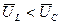 ) цепи переменного тока с активным сопротивлением, индуктивностью и ёмкостью
) цепи переменного тока с активным сопротивлением, индуктивностью и ёмкостью
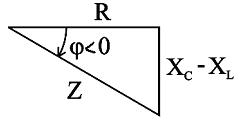
Рис.2.34. Треугольник сопротивлений цепи переменного тока с активным сопротивлением, индуктивностью и ёмкостью (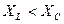 )
)
При XL < XC реактивное сопротивление X отрицательно и угол  < 0. Если UL = UC и XL = XC, то векторную диаграмму можно представить в виде рис. 2.35, а зависимость тока от частоты в виде рис.2.36.
< 0. Если UL = UC и XL = XC, то векторную диаграмму можно представить в виде рис. 2.35, а зависимость тока от частоты в виде рис.2.36.
В этом случае наступает резонанс напряжений, когда ток в цепи совпадает по фазе с напряжением источника. При этом угол  = 0, так как реактивное сопротивление равно нулю.
= 0, так как реактивное сопротивление равно нулю.

Рис.2.35. Векторная диаграмма резонанса напряжений 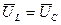
|
|
|

Рис.2.36. Зависимость тока от частоты питающей сети для резонанса напряжений
При резонансе напряжений частота источника равна собственной частоте колебаний LC -контура. Если 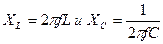 , где f - частота источника питания, то можно записать
, где f - частота источника питания, то можно записать 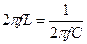 . Решив это уравнение относительно f, получим
. Решив это уравнение относительно f, получим
 . (2.34)
. (2.34)
На основании рис.2.35, 2.36 следует, что признаками резонанса напряжений являются:
а) полное сопротивление цепи равно активному сопротивлению Z = R;
б) ток в цепи совпадает по фазе с напряжением источника и имеет максимальное значение;
в) напряжение на индуктивной катушке равно напряжению на конденсаторе и каждое в отдельности превышает напряжение источника;
г) коэффициент мощности cos  = 1.
= 1.
На рис.2.37 изображены примерные функциональные зависимости индуктивных и емкостных напряжений, тока и коэффициента мощности в зависимости от изменения ёмкости конденсатора, где Cp - резонансная ёмкость.

Рис.2.37. Примерное изображение зависимостей UL, UC, 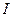 , cos
, cos  от изменения ёмкости конденсатора C
от изменения ёмкости конденсатора C
Количественная оценка соотношения энергий источника, катушки индуктивности и конденсатора при резонансе напряжений характеризуется добротностью контура:
 . (2.35)
. (2.35)
Величину 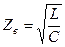 при резонансе называют волновым сопротивлением контура.
при резонансе называют волновым сопротивлением контура.
|
|
|
|
|
Дата добавления: 2014-11-29; Просмотров: 18256; Нарушение авторских прав?; Мы поможем в написании вашей работы!