
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Нормальные формы.
|
|
|
|
Для любой булевой функции можно построить таблицу истинности. Но и по таблице истинности можно восстановить булеву функцию. Различают совершенную дизъюнктивную (СДНФ) и совершенную конъюнктивную (СКНФ) нормальные формы. Обе они являются восстановленными булевыми функциями из исходной таблицы истинности.
Для получения СДНФ в таблице выбирают истинностные значения функции (она не должна быть тождественно-ложной) и соответствующие этим значениям переменные. Если значение переменной равно 0, то ее берут с отрицанием, если 1, то без отрицания и соединяют их конъюнкциями. Таким образом, организуются элементарные конъюнкции. Дизъюнкции элементарных конъюнкций образуют СДНФ.
Пример (*): Дана таблица истинности. Построить СДНФ.
| x | y | z | 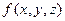
|
Функция принимает значение 1 на наборах значений переменных 101, 010, 001.
Этим наборам соответствуют элементарные конъюнкции:  .
.
В итоге получаем СДНФ: 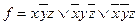 .
.
Для получения СКНФ среди значений функции из таблицы истинности выбирают нулевые (функция не должна быть тождественно-истинной) и соответствующие им переменные соединяют в элементарные дизъюнкции, причем, если переменная имеет 0 значение, то она берется без отрицания, если – 1 -- с отрицанием. Далее элементарные дизъюнкции соединяются знаками конъюнкции, и получается СКНФ.
Пример: Используя таблицу истинности предыдущего примера, составить СКНФ.
Функция принимает 0-значения при следующих комбинациях значений переменных: 111, 110, 100, 011, 000. Этим комбинациям соответствуют следующие элементарные дизъюнкции:  . Тогда СКНФ запишется в виде:
. Тогда СКНФ запишется в виде: 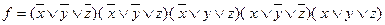 .
.
|
|
|
Задачи.
1. Построить СДНФ и СКНФ для функции, таблица истинности которой имеет следующий вид:
| x | y | z | f(x,y,z) |
2.3. Минимизация нормальных форм.
В виду того, что формулы СКНФ и СДНФ довольно громоздки, есть необходимость в их упрощении. Для этого существует алгоритм их минимизации. Но прежде нужно знать некоторые термины.
Функция g называется импликантом для функции f, если из равенства g=1 следует равенство f=1 при одном и том же наборе значений, входящих в них переменных.
Пример: Для функции 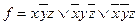 импликантом является функция
импликантом является функция 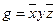 . Действительно, при x=0,y=1,z=0, значения обеих функций равны 1.
. Действительно, при x=0,y=1,z=0, значения обеих функций равны 1.
Функция  не является импликантом, т.к. при x=1,y=1,z=0 значения g=1,а f=0.
не является импликантом, т.к. при x=1,y=1,z=0 значения g=1,а f=0.
Импликант называется простым, если отбрасывание любой его переменной приводит к тому, что полученная функция перестает быть импликантом.
Пример:1) проверим импликант 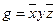 на простоту.
на простоту.
При исключении в нем переменной x получим функцию 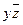 , которая принимает значение 1 при y=1,z=0. При этом функция f может принимать и нулевое значение (например, f(1,1,0)=0).
, которая принимает значение 1 при y=1,z=0. При этом функция f может принимать и нулевое значение (например, f(1,1,0)=0).
Исключив переменную y, получим функцию  , которая принимает значение 1 при x=0, z=0. Но при этом f может принимать и нулевые значения: f(0,0,0)=0.
, которая принимает значение 1 при x=0, z=0. Но при этом f может принимать и нулевые значения: f(0,0,0)=0.
Исключив z, получим функцию 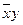 , которая принимает значение 1 при x=0,y=1. При этом f может в том числе принимать и нулевое значение (например,
, которая принимает значение 1 при x=0,y=1. При этом f может в том числе принимать и нулевое значение (например, 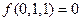 ).
).
Так как при исключении любой переменной функция 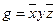 перестает быть импликантом функции f, то она является простым импликантом f.
перестает быть импликантом функции f, то она является простым импликантом f.
2) Функция  является импликантом для f, но не является простым, т.к. исключив из него x, снова получим импликант для f.
является импликантом для f, но не является простым, т.к. исключив из него x, снова получим импликант для f.
Выделив все простые импликанты и объединив их дизъюнкцией, получим сокращенную ДНФ (сокр. ДНФ f).
Для всякой функции (кроме тождественно-ложной) существует единственная сокращенная ДНФ.
|
|
|
Алгоритм построения сокр. ДНФ:
- По таблице истинности построить СКНФ функции f.
- В СКНФ раскрыть скобки и удалить дублирующие элементы, используя законы логики.
Пример: для функции f из примера 1 глава 3 построить сокр. ДНФ.
1) из таблицы истинности по известным правилам построили
СКНФf= 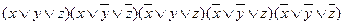 ;
;
2) раскрываем скобки, используя законы умножения и закон коммутативности (умножать лучше скобки, которые отличаются одной переменной). Поэтому меняем местами 2-ю и 3-ю скобки: 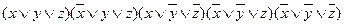 . Перемножим сначала 1-ю и 2-ю, затем 4-ю и 5-ю скобки, затем все остальное. Используем законы:
. Перемножим сначала 1-ю и 2-ю, затем 4-ю и 5-ю скобки, затем все остальное. Используем законы: 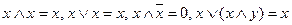 .
.
В результате получена сокр. ДНФ f =  .
.
Сокр. ДНФ f называется тупиковой (ТДНФ), если из дизъюнкции простых импликантов функции f нельзя отбросить ни одного слагаемого.
ТДНФ f, содержащая минимальное количество переменных и их отрицаний, называется минимальной ДНФ (МДНФ) функции f.
Алгоритм построения ТДНФ и МДНФ функции f:
- По таблице истинности строим СДНФ f.
- Строим сокр. ДНФ из СКНФ f.
- Каждому слагаемому сокр. ДНФ ставим в соответствие свой номер (в любом порядке).
- Составляем таблицу покрытий. Слагаемые СДНФ в 1-й строке, слагаемые сокр. ДНФ – в 1-м столбце. Если слагаемое сокр. ДНФ целиком содержится в слагаемом СДНФ, то в клетке на пересечении пишем соответствующий номер из п.3.
- Составляем решеточное выражение. В каждом столбце числа соединяем знаком дизъюнкции и окончательно получаем конъюнкцию этих дизъюнкций.
- Раскрываем скобки конъюнкции, используя закон поглощения.
- Заменяем номера на соответствующие слагаемые сокр. ДНФ. Полученное выражение называется ТДНФ.
- ТДНФ с минимальным числом переменных и их отрицаний являются МДНФ функции f.
Пример: Построить ТДНФ и МДНФ для f из примера 1 гл.3.
Из предыдущих примеров СДНФ 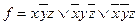
Сокр. ДНФ f =  .
.
Строим таблицу покрытий:
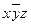
| 
| 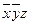
| |
 (1) (1)
| |||
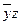 (2) (2)
|
Решеточное выражение равно:  =ТДНФ. Поскольку в решеточном выражении слагаемое одно, то ТДНФ является и МДНФ функции f.
=ТДНФ. Поскольку в решеточном выражении слагаемое одно, то ТДНФ является и МДНФ функции f.
Для построения минимальной конъюнктивной нормальной формы (МКНФ) функции f нужно построить МДНФ функции 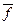 и в полученной МДНФ заменить знак
и в полученной МДНФ заменить знак 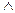 на знак
на знак  и наоборот, а над каждой переменной поставить знак отрицания. Это и будет МКНФ функции f.
и наоборот, а над каждой переменной поставить знак отрицания. Это и будет МКНФ функции f.
|
|
|
Для получения минимальной нормальной формы (МНФ) функции f строят все МДНФ и МКНФ. Из них выбирают форму с наименьшим числом переменных и отрицаний переменных. Это и есть МНФ функции f.
Задачи.
- Показать, что для функции f из примера (*) функция y=
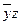 является импликантом.
является импликантом. - Для функции из задачи 1 главы 3 построить сокращенную ДНФ.
- Используя данные предыдущей задачи построить тупиковую и минимальную ДНФ функции f.
- Используя данные задачи 2 построить минимальную КНФ функции f.
- Построить минимальную нормальную форму функции f из примера (*).
2.4. Контактные схемы.
Контактные схемы – это устройства релейно–контактного действия, широко используемые в ЭВМ. Они состоят из переключателей, соединяющих проводов и полюсов (вход в систему, выход из системы). Каждый переключатель может находиться в одном из двух состояний: замкнутом – 1(ток проходит) и разомкнутом – 0 (ток не проходит). Поэтому переключатели представляют собой булевы функции.
Каждой контактной схеме можно поставить в соответствие некоторую булеву функцию. Наоборот, булева функция реализуется некоторой контактной схемой.
Пусть функции f(x)=x соответствует контактная схема: ------ x ------
Тогда логическим операциям над f(x) соответствуют следующие схемы:
-----  ---- -- отрицание;
---- -- отрицание;
-----x----y---- -- конъюнкция;
 x
x
y -- дизъюнкция

Пример: Контактная схема функции 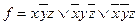 имеет вид:
имеет вид:
 x
x  z
z
 y
y 

 z
z
Законы математической логики позволяют минимизировать функцию (МНФ), исключив лишние переменные. В итоге контактная схема будет содержать наименьшее число переключателей.
МНФ f=  . Тогда упрощенная контактная схема примет вид:
. Тогда упрощенная контактная схема примет вид:
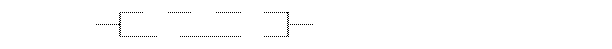
 y
y 
 z
z
Задачи.
- Реализовать контактной схемой функцию из примера (*).
- Решить проблему минимизации для контактной схемы предыдущей задачи.
2.5. Логика предикатов.
Предикатом называют логическую функцию одной или нескольких переменных, при замене которых конкретными значениями обращают его в высказывание. В зависимости от количества переменных различают одноместный, двухместный, n-местный предикаты.
|
|
|
Пример: P(x)= «x – простое число» -- одноместный предикат, P(2)= «2 – простое число» -- истинное высказывание(1), P(4)= «4 – простое число» -- ложное высказывание(0).
Q(x,y)= « » -- двухместный предикат, Q(1,2)= «1>2;
» -- двухместный предикат, Q(1,2)= «1>2; 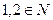
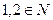 » -- ложное высказывание(0), Q(2,1)= «2>1; 2,1
» -- ложное высказывание(0), Q(2,1)= «2>1; 2,1 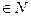 » -- истинное высказывание(1).
» -- истинное высказывание(1).
Замена части предикатных неизвестных обращает его в предикат меньшей местности. Замена вех переменных – в высказывание. Высказывание при этом является 0-местным предикатом.
Совокупность всех значений переменных, обращающих предикат в истинное высказывание образуют множество истинности данного предиката.
По аналогии с высказываниями, к предикатам применяются операции отрицания, дизъюнкции, конъюнкции, импликации и эквивалентности. Указанные операции обращают предикат в предикат.
Есть возможность обратить предикат в высказывание с помощью так называемых кванторов общности и существования:
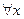 (для всех x) – квантор общности;
(для всех x) – квантор общности;
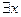 (существует такое значение x) – квантор существования.
(существует такое значение x) – квантор существования.
Пример: P(x)= «x – простое число» -- одноместный предикат,
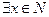 P(x) – истинное высказывание,
P(x) – истинное высказывание,
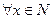 P(x) – ложное высказывание.
P(x) – ложное высказывание.
Если все предикатные переменные связаны кванторами, то предикат обращается в высказывание, если часть, то в предикат меньшей местности. Операция приписывания к предикату квантора называется навешиванием квантора. Переменная, к которой относится квантор, называется связанной, без квантора – свободной.
Пример: P(x,y,z)= « » -- трехместный предикат,
» -- трехместный предикат,
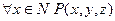 -- двухместный предикат,
-- двухместный предикат,
 -- одноместный предикат,
-- одноместный предикат,
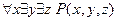 -- истинное высказывание.
-- истинное высказывание.
Задачи.
- Определить, чему равны значения предиката Р(x)= «x – четное число» при x=23 и x=48.
- Применить кванторы общности и существования к предикату примера 1 и найти значения полученных высказываний.
- Навесить квантор общности на все переменные предиката P(x,y)= «x делится на y без остатка» и определить значение высказывания.
- Навесить квантор существования на все переменные предиката P(x,y)= «x делится на y без остатка» и определить значение высказывания.
|
|
|
|
|
Дата добавления: 2014-11-29; Просмотров: 949; Нарушение авторских прав?; Мы поможем в написании вашей работы!