Цилиндрические и сферические координаты

Полярная система координат в пространстве.

Рассмотрим в пространстве координатную плоскость Р, на которой задана полярная система координат. Пусть Oz – координатная ось, перпендикулярная плоскости Р и пересекающая ее в полюсе О. Координатная ось Oz направлена так, чтобы из конца положительного направления оси Oz направление отсчета положительных значений полярного угла φ от полярной оси Ох было видно против часовой стрелки. Совокупность этих элементов называется полярной системой координат в пространстве (рис.3.2).

Координатная плоскость Р называется экваториальной, а координатная ось Oz – зенитной. Для удобства будем полагать, что масштабные отрезки одинаковы (ОЕ ₁ = ОЕ ₂) и точка отсчета О координатной оси Oz совпадает с полюсом О.

Цилиндрическими координатами точки М, не лежащими на зенитной оси, называется упорядоченная тройка чисел ρ, φ, z, где ρ и φ – полярные координаты ортогональной проекции М_р точки М на экваториальную плоскость, а z – координата на зенитной оси Oz проекции М_z точки М на зенитную ось (рис. 3.3). Для точек зенитной оси считают ρ = 0, φ – любое число, а z определяется так, как указано выше. Тот факт, что ρ, φ и z есть цилиндрические координаты точки М в пространстве, записывают так: М (ρ, φ, z).

Заметим, что при помощи цилиндрических координат не устанавливается взаимно однозначного соответствия между множеством всех точек геометрического пространства и множеством упорядоченных троек действительных чисел.

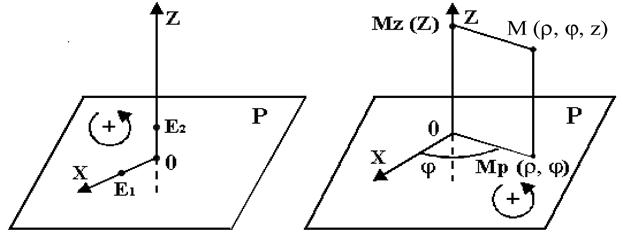
Рис. 3.2 Рис. 3.3

Сферическими координатами точки М, не лежащей на зенитной оси, называется упорядоченная тройка чисел r, φ, Θ, где r – длина отрезка ОМ, φ – угол от полярной оси Ох до луча ОМ_р (М_р – проекция точки М на экваториальную плоскость), а Θ – угол между лучами ОМ_р и ОМ, который принимает значения в интервале 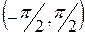, причем считается, что Θ = 0, если точка М лежит в экваториальной плоскости, Θ > 0, если луч ОМ образует острый угол с зенитной осью, и Θ < 0, если луч ОМ образует тупой угол с зенитной осью (рис.3.4).

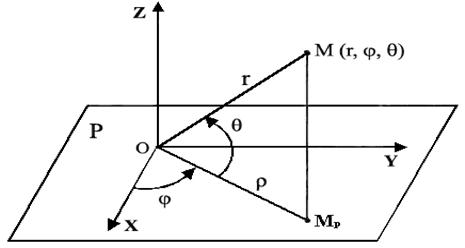
Рис. 3.4

Если точка М лежит на зенитной оси и не совпадает с полюсом О, то считают, что φ – любое число, а или 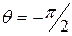в зависимости от того, совпадает ли направление луча ОМ с направлением зенитной оси или противоположно ему. Для полюса считают r = 0, φ и Θ – любые числа. При помощи сферических координат не устанавливается взаимно однозначного соответствия между множеством всех точек пространства и множеством упорядоченных троек действительных чисел.

Найдем зависимости между прямоугольными декартовыми координатами точки М (х, у, z) и ее цилиндрическими координатами М (ρ, φ, z) и сферическими координатами М (r, φ, θ). Введем декартову прямоугольную систему координат, принимая за положительную полуось Ох полярную ось, за ось Оу – ось, полученную из оси Ох поворотом ее вокруг полюса в экваториальной плоскости на угол 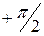и зенитную ось за ось Оz (рис.3.4.).

Из рис.3.4, учитывая формулы (1.7) и рис.3.3. находим

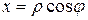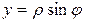, , z= z (1.12)

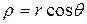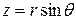C другой стороны, , а , значит,

(1.13)

Формулы (1.12) и (1.13) верны и для того случая, когда точка М лежит на зенитной оси и когда она совпадает с полюсом (при дополнительных соглашениях о величинах ρ и φ в этом случае).

По формулам (1.12) вычисляются декартовы прямоугольные координаты точки М в случае, если известны ее цилиндрические координаты, а по формулам (1.13) – если известны ее сферические координаты.

Из формул (1.13) следует, что

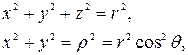
откуда

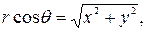
значит,

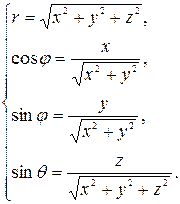(1.14)

По этим формулам вычисляются сферические координаты r, φ, Θ точки М, не лежащей на зенитной оси по ее декартовым прямоугольным координатам x, y, z (при указанном взаимном расположении этих двух систем координат).

Цилиндрические координаты ρ, φ, z точки М вычисляются по ее декартовым прямоугольным координатам x, y, z из формул (1.12) с учетом формул (1.8) и (1.9) или (1.10).

Аналогично декартовым координатам определяется уравнение поверхности в сферических координатах: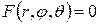

и в цилиндрических координатах .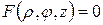

Замечание. Вторую сферическую координату φ часто называют долготой, третью Θ – широтой. Иногда вместо широты Θ рассматривают угол ψ между положительным направлением зенитной оси и лучом ОМ, идущим из полюса О в данную точку М; величина ψ изменяется в пределах от 0 до π. Величина ψ называется зенитным расстоянием.

Так как 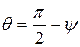, то в формулах (1.13) и (1.14) (в случае, если за третью сферическую координату принимается зенитное расстояние) 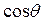и 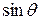следует заменить соответственно на 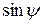и .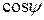

ГЛАВА 2

Дата добавления: 2014-11-29