
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Кинематика точки. Трение скольжения.Сопротивление, возникающее при скольжении соприкасающихся шероховатых тел, называется трением скольжения
|
|
|
|
Трение
Трение скольжения. Сопротивление, возникающее при скольжении соприкасающихся шероховатых тел, называется трением скольжения.
 Рассмотрим тело весом
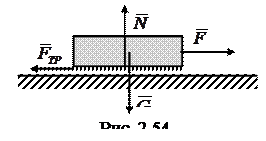
Рассмотрим тело весом 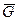 , находящееся в покое на негладкой горизонтальной плоскости (рис. 2.54). Попытка передвинуть тело, приложив к нему горизонтальную силу
, находящееся в покое на негладкой горизонтальной плоскости (рис. 2.54). Попытка передвинуть тело, приложив к нему горизонтальную силу  , не приводит к успеху до тех пор, пока величина силы не достигнет некоторого значения
, не приводит к успеху до тех пор, пока величина силы не достигнет некоторого значения 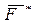 . Равнодействующая сил реакций опоры может быть представлена в виде двух составляющих - силы нормального давления
. Равнодействующая сил реакций опоры может быть представлена в виде двух составляющих - силы нормального давления 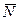 и силы трения покоя
и силы трения покоя 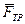 .
.
Опыт показывает, что 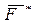 и
и 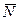 связаны соотношением:
связаны соотношением:
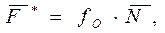
где 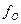 - статический коэффициент трения; зависящий от материалов соприкасающихся тел и состояния их поверхностей.
- статический коэффициент трения; зависящий от материалов соприкасающихся тел и состояния их поверхностей.
Пока 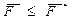 , тело будет оставаться в покое. Если же к нему приложить силу, большую чем
, тело будет оставаться в покое. Если же к нему приложить силу, большую чем 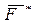 , то оно станет двигаться.
, то оно станет двигаться.
При движении силу сопротивления можно найти, пользуясь формулой
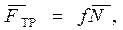 (2.72)
(2.72)
где  - динамический коэффициент трения, a
- динамический коэффициент трения, a 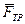 — силой трения скольжения.
— силой трения скольжения.
Сила трения всегда направлена вдоль поверхностей соприкосновения в сторону, противоположную относительному движению. Она всегда меньше силы нормального давления. Представление о величине коэффициента трения для некоторых материалов приведены ниже:
| Материал контактирующих поверхностей | коэффициент трения статический – fО | коэффициент трения скольжения - f | ||
| сухое | со смазкой | с водяной смазкой | ||
| Сталь / сталь | 0,15 | 0,1 | 0,01 | - |
| Металл / дерево | 0,5÷0,6 | 0,4÷0,5 | 0,03÷0,08 | 0,25 |
| Дерево / дерево | 0,065 | 0,3 | 0,1 | 0,28 |
| Кожа /серый чугун | 0,56 | 0,28 | 0,12 | - |
| Кожа / дерево | 0,47 | 0,27 | - | - |
| Сталь / лед | - | - | - | 0,014 |
| Автомобильная шина / асфальт | 0,55 | 0,3 | 0,15 |
Отметим, что динамический коэффициент трения всегда меньше статического коэффициента трения: f < f0. Оба зависят от состояния контактирующих поверхностей и слоя смазки между ними.
|
|
|
 Трения качения. Трением качения называется сопротивление, возникающее при качении одного тела по другому. Рассмотрим диск радиусом R, покоящийся на негладкой горизонтальной плоскости (рис. 2.55). Попытка перекатить диск, приложив к его центру горизонтальную силу F, не приведет к успеху, пока величина силы остается меньше предельного значения F**.
Трения качения. Трением качения называется сопротивление, возникающее при качении одного тела по другому. Рассмотрим диск радиусом R, покоящийся на негладкой горизонтальной плоскости (рис. 2.55). Попытка перекатить диск, приложив к его центру горизонтальную силу F, не приведет к успеху, пока величина силы остается меньше предельного значения F**.
Силы реакции опоры, распределенные по малой поверхности вблизи точки контакта Р, в соответствии с теоремой о приведении системы сил к центру могут быть заменены эквивалентной системой — силой нормального давления 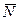 , силой трения покоя
, силой трения покоя 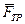 , приложенными в точке контакта - Р, а также парой сил трения качения с моментом
, приложенными в точке контакта - Р, а также парой сил трения качения с моментом  .
.
При равновесии диска из уравнения моментов относительно центра Р следует
FR = Мтр.
Опыт показывает, что F** и N связаны соотношением F** = δN/R, при этом
Мтр = δN. (2.73)
Размерный коэффициент δ [м] называется коэффициентом трения качения.
Поверхность качения называют абсолютно шероховатой, если  ≠ 0 и δ = 0.
≠ 0 и δ = 0.
Опыт показывает, что при прочих равных условиях F* много больше F**, поэтому в технике при необходимости уменьшить потери на трение стремятся заменить скольжение качением.
Значения коэффициента трения качения для некоторых материалов приведены ниже:
| Материал контактирующих поверхностей | коэффициент трения качения – δ (м) |
| Дерево по дереву | 0.5÷0.8 10-3 |
| Сталь мягкая по стали (колесо по рельсу) | 0.05 10-3 |
| Сталь закаленная по стали (шариковый подшипник) | 0.01 10-3 |
Сила внутреннего трения возникает между слоями одного и того же сплошного тела (жидкости или газа). Силы внутреннего (вязкого) трения зависят от относительной скорости смещения отдельных слоев газа или жидкости друг относительно друга. Например, вязкое трение возникает при течении жидкости или газа по трубам
|
|
|
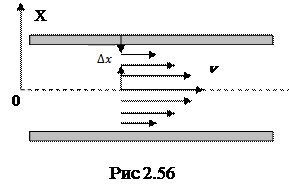 со скоростью
со скоростью 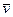 (рис. 2.56).
(рис. 2.56).
Скорость слоев жидкости уменьшается при приближении их к стенкам трубы. Отношение разности скоростей 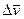 в двух близких слоях, расположенных на расстоянии
в двух близких слоях, расположенных на расстоянии 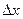 , называется средним градиентом скорости.
, называется средним градиентом скорости.
В одномерной задаче, когда 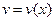 , средняя сила внутреннего трения
, средняя сила внутреннего трения
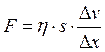 , (2.74)
, (2.74)
где 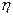 - коэффициент внутреннего трения,
- коэффициент внутреннего трения, 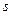 - площадь взаимодействующих слоев жидкости,
- площадь взаимодействующих слоев жидкости,  - средний градиент скорости.
- средний градиент скорости.
Коэффициент внутреннего трения зависит от агрегатного состояния вещества и температуры вещества:
| Вещество | Вода | Водяной пар | Машинное масло | Воздух |
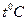
| ||||
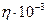 Па*с Па*с
| 1,0 | 0,013 | 0,018 |
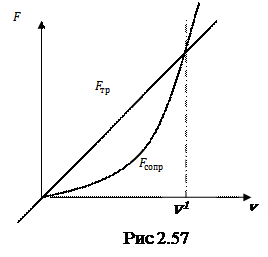 Сила сопротивления среды. При движении твердых тел в жидкости или газе, кроме силы внутреннего трения, на тело (в случае небольших скоростей и размеров тел) начинает оказывать существенное влияние сопротивление среды
Сила сопротивления среды. При движении твердых тел в жидкости или газе, кроме силы внутреннего трения, на тело (в случае небольших скоростей и размеров тел) начинает оказывать существенное влияние сопротивление среды
 (2.75)
(2.75)
где v - скорость движения тела; 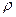 - плотность среды (жидкости или газа);
- плотность среды (жидкости или газа); 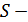 площадь поперечного сечения тела,
площадь поперечного сечения тела,  коэффициент сопротивления.
коэффициент сопротивления.
Тело, движущееся в среде, испытывает действие двух сил: силы вязкого трения (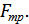 ) и силы сопротивления (
) и силы сопротивления (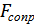 ). При небольших скоростях сила сопротивления меньше силы вязкого трения, а при больших – значительно превосходит её (рис. 2.57).
). При небольших скоростях сила сопротивления меньше силы вязкого трения, а при больших – значительно превосходит её (рис. 2.57).
При некотором значении скорости  силы
силы 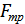 и
и 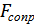 становятся равными по модулю.
становятся равными по модулю.
Сила сопротивления среды зависит от формы движущегося тела. Форму тела, при которой сила сопротивления мала, называют обтекаемой. Ракетам, самолетам, автомобилям и другим машинам, движущимся с большими скоростями в воздухе или воде, придают обтекаемую, каплеобразную форму.
 Задача 2.9
Задача 2.9
К вертикальной стене приставлена легкая лестница АВ, опирающаяся своим нижним концом на горизонтальный пол (рис..2.58). Коэффициент трения покоя лестницы о стену f1, о пол f2. Сила тяжести поднимающегося по ней человека 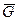 .
.
Определить реакции стены 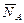 и пола
и пола 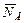 , а также наименьший угол а, образуемый лестницей с полом в положении равновесия. Силой тяжести лестницы пренебречь.
, а также наименьший угол а, образуемый лестницей с полом в положении равновесия. Силой тяжести лестницы пренебречь.
Решение. При нахождении на лестнице человека точка В лестницы стремится скользить вправо, а точка А — вниз. Отбрасывая связи, (пол и стену), покажем реакции, действующие на лестницу: нормальные 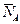 и
и 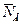 , а также силы трения
, а также силы трения 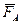 и
и 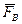 . Система сил, действующих на лестницу, плоская произвольная. Составим уравнения равновесия:
. Система сил, действующих на лестницу, плоская произвольная. Составим уравнения равновесия:
|
|
|
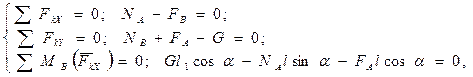 (*)
(*)
где l = ВС; l = АВ – длина лестницы.
Система уравнений (*)пока статически не определима, так как содержит пять неизвестных: NA., NB, FA, FB и α. Но силы покоя связаны с нормальными реакциями законом Кулона:
 (**)
(**)
Таким образом, после добавления зависимостей (**) система уравнений становится статически определимой. Из первых двух уравнений системы (*) находим:

Исключая реакцию NA, запишем 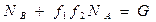 , откуда
, откуда 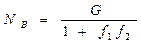 .
.
Подставляя NB в уравнение NA – f2NB = 0, рассчитаем реакцию 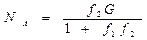 .
.
Из полученных выражений следует, что реакции NA и NB не зависят от положения человека на лестнице.
Решая третье уравнение системы (*), найдем
 .
.
Подставляя значения NA и FA =f1NA, получим
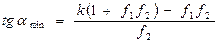 ,
,
где через k обозначено отношение l1/l.
Лестница будет находиться в равновесии при угле установки 900>α>αmin. Каждому положению человека на лестнице (значению k = l1/l) отвечает свой минимально возможный угол ее установки.
 Таким образом, при решении задач на равновесие твердых тел при учете сил трения необходимо к уравнениям равновесия присоединить опытные зависимости сил трения от сил нормального давления, например даваемые законом Кулона. Особенность получаемого решения состоит в том, что искомая величина имеет целый диапазон значений, при котором рассматриваемое тело находится в равновесии.
Таким образом, при решении задач на равновесие твердых тел при учете сил трения необходимо к уравнениям равновесия присоединить опытные зависимости сил трения от сил нормального давления, например даваемые законом Кулона. Особенность получаемого решения состоит в том, что искомая величина имеет целый диапазон значений, при котором рассматриваемое тело находится в равновесии.
Задача 2.10
На валу барабана (рис. 2.57) радиусом R, поднимающего груз, сила тяжести которого 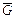 , находится колодочный тормоз, причем радиус барабана тормоза равен r. Определить минимально необходимую силу прижатия колодок для удержания груза, если коэффициент трения колодок о тормозной барабан f.
, находится колодочный тормоз, причем радиус барабана тормоза равен r. Определить минимально необходимую силу прижатия колодок для удержания груза, если коэффициент трения колодок о тормозной барабан f.
Решение. Составим уравнение равновесия барабана
ΣMO=GR - 2FТР r =0,
где FТР — сила трения колодки о тормозной барабан.
Сила прижатия колодки связана с силой трения законом Кулона: FТР =f P. Решая совместно написанные уравнения, определим
 .
.
Равновесие барабана будет иметь место при значениях силы прижатия колодок, отвечающих условию
|
|
|
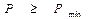 .
.
 Задача 2.11
Задача 2.11
Цилиндрический каток (рис. 2.58) радиусом R, сила тяжести которого 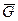 , приводится в движение посредством силы
, приводится в движение посредством силы 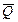 , приложенной к нити, намотанной на барабан катка радиусом r. Угол схода нити с барабана α, коэффициент трения качения δ, коэффициент сцепления катка с поверхностью качения fСЦ. Определить нормальную реакцию
, приложенной к нити, намотанной на барабан катка радиусом r. Угол схода нити с барабана α, коэффициент трения качения δ, коэффициент сцепления катка с поверхностью качения fСЦ. Определить нормальную реакцию 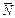 , силу сцепления
, силу сцепления 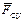 и силу
и силу  , необходимую для равномерного качения катка без скольжения.
, необходимую для равномерного качения катка без скольжения.
Решение. Освобождая каток от связи - поверхности движения, покажем ее действие на каток в виде нормальной реакции 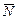 , смещенной вперед по ходу движения катка на величину коэффициента трения качения δ, и горизонтальной реакции
, смещенной вперед по ходу движения катка на величину коэффициента трения качения δ, и горизонтальной реакции 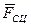 . Рассмотрим равновесие катка, находящегося под действием активных сил
. Рассмотрим равновесие катка, находящегося под действием активных сил  и
и 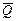 , а также реакций связи
, а также реакций связи 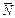 и
и 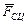 . Запишем уравнения равновесия катка в проекциях на оси координат, показанных на рис. 2.58. Уравнение моментов составим относительно центра катка С:
. Запишем уравнения равновесия катка в проекциях на оси координат, показанных на рис. 2.58. Уравнение моментов составим относительно центра катка С: 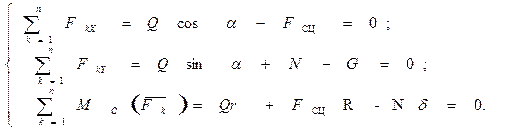
Из первого уравнения системы уравнений равновесия найдем силу сцепления 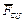 и подставим ее в третье. Получим Q(r+R cosα) - N δ =0. Исключим из написанного уравнения нормальную реакцию
и подставим ее в третье. Получим Q(r+R cosα) - N δ =0. Исключим из написанного уравнения нормальную реакцию 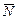 , найдя ее из второго уравнения системы уравнений равновесия:
, найдя ее из второго уравнения системы уравнений равновесия:
N = G – Q sinα;
Q (r+R cosα) - G δ+δ Q sinα = 0.
Определим силу 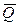
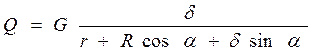 .
.
Подставив значение 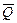 в первое уравнение системы, рассчитаем
в первое уравнение системы, рассчитаем
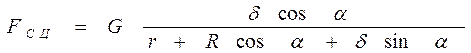
Далее с учетом выражения для 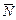 найдем
найдем

Определим максимальную силу сцепления по закону Кулона

Каток будет катиться без скольжения, если имеет место неравенство
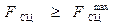
или 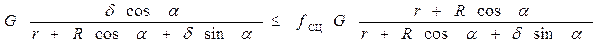
Упрощая неравенство, получим условие качения катка без скольжения
δ cosα ≤ (r+R cosα) fСЦ.
Вывод
В данной главе изложены основы теоретической механики, без понимания которых практически невозможно двигаться далее и изучать более сложные разделы механики.
Любая задача механики оперирует понятием абсолютно свободного тела. Поскольку окружающие нас тела не могут быть абсолютно свободными, то определения связей, наложенных на изучаемый объект, и приведение их к схематичному виду с дальнейшей заменой реактивными силами становится насущно необходимым. Пока не расположены все силы (включая реактивные) применительно к объекту, невозможно описать его равновесие (в противном случае получим неверный ответ и, как следствие, проблему, размеры которой будут зависеть от поставленной задачи).
Красной нитью через всю механику проходит понятие момента силы. Его точное определение облегчит дальнейшее усвоение материала. С этим понятием тесно связана теорема Вариньона, которую можно воспринимать как следствие или первооснову уравнений равновесия. Также в главе рассмотрены способы расчёта ферм, как наиболее распространённых конструкций и первая задача любого механика: определение положения центра тяжести тела и осей (плоскостей) симметрии. Завершается глава темой о силе трения – основе движения материальных тел.
Контрольные вопросы
1. Перечислите основные системы сил.
2. Что такое реактивная сила?
3. Сформулируйте условия и уравнения равновесия.
4. Что такое момент силы относительно точки и относительно оси?
5. Как расположен вектор момента силы?
6. Сформулируйте методы расчёта усилий в стержнях ферм.
7. Назовите способы определение положения центра тяжести твёрдого тела.
8. Что такое сила трения скольжения и чем она отличается от силы сцепления?
9. Опишите механизм возникновения силы трения качения.
ГЛАВА 3 ОСНОВЫ КИНЕМАТИКИ
Кинематика - раздел теоретической механики, в котором изучают движение материальных объектов вне зависимости от причин, вызывающих это движение.
Чтобы охарактеризовать движение какой-либо точки или тела относительно другого, необходимо связать с последним систему координат, которая вместе с этим телом образует систему отсчета.
Задачи кинематики: изучение видов движения материальных объектов - материальной точки и тел; выбор способа описания их движения при помощи уравнений, которые определяли бы положение этих объектов относительно системы отсчета в любой момент времени; определение зависимости между различными кинематическими величинами - скоростями и ускорениями в целом.
Существует три способа описания движения точки: векторный, координатный и естественный. Рассмотрим их последовательно.
Векторный способ. В этом способе положение интересующей нас точки А задают радиусом-вектором 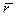 , проведенным из некоторой неподвижной точки О выбранной системы отсчета в точку А. При движении точки А ее радиус-вектор меняется в общем случае как по величине, так и по направлению, т. е. радиус-вектор
, проведенным из некоторой неподвижной точки О выбранной системы отсчета в точку А. При движении точки А ее радиус-вектор меняется в общем случае как по величине, так и по направлению, т. е. радиус-вектор 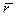 зависит от времени t.
зависит от времени t.
 Введем понятие скорости точки. Пусть за промежуток времени Δ t точка А переместилась из точки 1 в точку 2(рис. 3.1).
Введем понятие скорости точки. Пусть за промежуток времени Δ t точка А переместилась из точки 1 в точку 2(рис. 3.1).
Из рисунка видно, что вектор перемещения 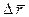 точки А представляет собой приращение радиуса-вектора
точки А представляет собой приращение радиуса-вектора 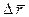 за время Δ t. Отношение
за время Δ t. Отношение 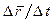 называют средним вектором скорости
называют средним вектором скорости 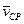 за время Δ t. Вектор
за время Δ t. Вектор 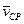 совпадает по направлению с вектором
совпадает по направлению с вектором 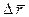 . Определим теперь вектор скорости
. Определим теперь вектор скорости  точки в данный момент времени как предел отношения
точки в данный момент времени как предел отношения 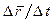 при
при  , т. е.
, т. е.
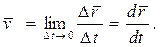 . (3.1)
. (3.1)
Это значит, что вектор скорости  точки в данный момент времени равен
точки в данный момент времени равен
производной от радиуса-вектора 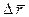 по времени и направлен по касательной к траектории в данной точке в сторону движения точки А (как и вектор
по времени и направлен по касательной к траектории в данной точке в сторону движения точки А (как и вектор 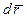 ).
).
Модуль вектора 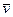 равен*
равен*
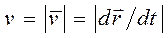 .
.
Другим важным понятием, характеризующим движение точки, является ускорение. Вектор ускорения 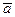 определяет скорость изменения вектора скорости точки со временем:
определяет скорость изменения вектора скорости точки со временем:
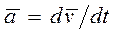 . (3.2)
. (3.2)
Таким образом, зная зависимость 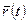 , можно найти как скорость
, можно найти как скорость  , так и ускорение
, так и ускорение 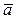 точки в каждый момент времени.
точки в каждый момент времени.
Задача 3.1
Радиус-вектор точки зависит от времени t по закону 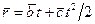 , где
, где 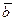 и
и 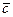 - постоянные векторы. Найдем скорость
- постоянные векторы. Найдем скорость  и ускорение
и ускорение 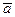 точки:
точки:
 ,
, 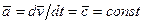 .
.
Модуль вектора скорости 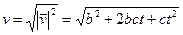 .
.
Возникает и обратная задача: можно ли найти  и
и 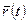 , зная зависимость от времени ускорения
, зная зависимость от времени ускорения 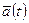 ?
?
Оказывается, для получения однозначного решения этой задачи одной зависимости 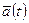 недостаточно; необходимо еще знать начальные условия, а именно скорость
недостаточно; необходимо еще знать начальные условия, а именно скорость 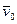 и радиус-вектор
и радиус-вектор  точки в некоторый начальный момент времени t= 0. Чтобы в этом убедиться, рассмотрим простейший случай, когда ускорение точки в процессе движения
точки в некоторый начальный момент времени t= 0. Чтобы в этом убедиться, рассмотрим простейший случай, когда ускорение точки в процессе движения 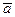 = const.
= const.
Сначала определим скорость точки  . Согласно (3.2) за промежуток времени dt элементарное приращение скорости точки
. Согласно (3.2) за промежуток времени dt элементарное приращение скорости точки 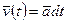 . Проинтегрировав это выражение по времени от t= 0 до t, найдем приращение вектора скорости за это время:
. Проинтегрировав это выражение по времени от t= 0 до t, найдем приращение вектора скорости за это время:
 .
.
Найденная величина 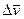 - это еще не искомая скорость
- это еще не искомая скорость  . Чтобы найти
. Чтобы найти  ,
,
необходимо знать скорость 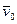 в начальный момент времени, тогда
в начальный момент времени, тогда
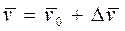 ,
,
или
 .
.
________________________
*Заметим, что в общем случае 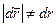 , где
, где 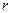 модуль радиуса – вектора
модуль радиуса – вектора  и
и 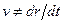 . Например, если
. Например, если  меняется только по направлению (точка движется по окружности), то
меняется только по направлению (точка движется по окружности), то  ,
, 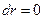 , но
, но 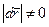 .
.
Аналогично решается вопрос и о радиус-векторе точки 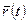 . Согласно (3.1), за промежуток времени dt элементарное приращение радиус-вектора точки будет
. Согласно (3.1), за промежуток времени dt элементарное приращение радиус-вектора точки будет 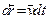 . Интегрируя это выражение с учетом найденной зависимости
. Интегрируя это выражение с учетом найденной зависимости  , определим приращение радиус-вектора за время от t= 0 до t:
, определим приращение радиус-вектора за время от t= 0 до t: 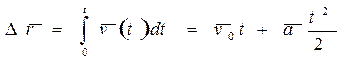 .
.
Для нахождения самого радиус-вектора 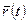 необходимо знать еще положение точки
необходимо знать еще положение точки  в начальный момент времени. Тогда
в начальный момент времени. Тогда
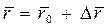 ,
,
или
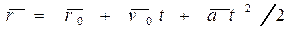 .
.
 Рассмотрим, например, движение камня А, брошенного под некоторым углом к горизонту с начальной скоростью
Рассмотрим, например, движение камня А, брошенного под некоторым углом к горизонту с начальной скоростью 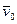 . Если считать, что камень движется с постоянным ускорением
. Если считать, что камень движется с постоянным ускорением 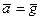 , то его положение относительно точки бросания (
, то его положение относительно точки бросания (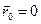 ) определяется радиус-вектором
) определяется радиус-вектором
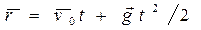 ,
,
т. е. в данном случае 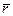 представляет собой сумму двух векторов, что показано на рис. 3.2
представляет собой сумму двух векторов, что показано на рис. 3.2
Итак, для полного решения задачи о движении точки, определения ее скорости  и положения
и положения 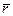 в зависимости от времени недостаточно знать зависимость
в зависимости от времени недостаточно знать зависимость 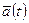 , но еще необходимо знать и начальные условия, т. е. скорость
, но еще необходимо знать и начальные условия, т. е. скорость 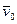 и положение
и положение 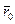 точки в начальный момент времени.
точки в начальный момент времени.
Координатный способ. Запишем проекции на оси X, Y, Z радиуса-вектора 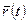 , характеризующего положение интересующей нас точки относительно начала координат О в момент времени t:
, характеризующего положение интересующей нас точки относительно начала координат О в момент времени t:

Зная зависимость этих координат от времени - закон движения точки, можно найти как положение точки в каждый момент времени, так ее скорость и ускорение. Действительно, спроектировав (3.1) и (3.2), например, на ось X, получим формулы, определяющие проекции вектора скорости и вектора ускорения на эту ось:
vx = dx/dt, (3.3)
где dx - проекция вектора перемещения dr на ось X;
ax = dvx/dt = d2x/dt2, (3.4)
где dvx - проекция вектора приращения скорости 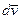 на ось X.
на ось X.
Аналогичные соотношения получаются для Y и Z - проекций соответствующих векторов. Из этих формул видно, что проекции векторов скорости и ускорения равны соответственно первой и второй производным координат по времени.
Таким образом, зависимости x(t), y(t), z(t) по существу полностью определяют движение точки. Зная их, можно найти не только положение точки, но и проекции ее скорости и ускорения, а следовательно, модуль и направление векторов 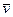 и
и 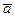 в любой момент времени. Например, модуль вектора скорости,
в любой момент времени. Например, модуль вектора скорости,
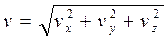 ;
;
направление же вектора 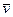 задается направляющими косинусами по формулам
задается направляющими косинусами по формулам
 ,
,
где α, β, γ — углы между вектором 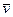 и осями X, Y, Z соответственно.
и осями X, Y, Z соответственно.
Аналогичными формулами определяются модуль и направление вектора ускорения.
Кроме того, можно решить и ряд других вопросов: найти траекторию точки, зависимость пройденного ею пути от времени, зависимость скорости от положения точки и пр.
Решение обратной задачи - нахождение скорости и закона движения точки по заданному ускорению - проводится, как и в векторном способе, путем интегрирования (в данном случае проекций ускорения по времени), причем задача и здесь имеет однозначное решение, если кроме ускорения заданы еще и начальные условия - проекции скорости и координаты точки в начальный момент.
Задача 3.2
Движение точки задано в координатной форме: x = t/2; y = t2 +2, где х, у — координаты, м. В начальный момент времени t0 = 0.
Рассчитать траекторию точки, а также скорость и ускорение для любого момента времени.
Решение. Проведем решение в три этапа.
1. Расчет траектории, начального положения точки и направления ее движения. Найдем из первого уравнения движения время t = 2х и, подставив во второе, получим уравнение траектории точки М (рис. 3.3), представляющей собой параболу:
у = 4х2+2.
Для определения ветви параболы, по которой движется точка, проанализируем уравнение движения х = t/2. Так как время возрастает от t = 0, координата х положительна и возрастает от xо = 0. Следовательно, точка движется по правой ветви параболы.
2. Расчет скорости.
Определим проекции скорости на оси координат:
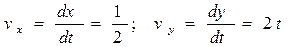 .
.
Найдем модуль скорости (м/с)
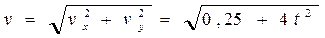 .
.
Рассчитаем направляющие косинусы:

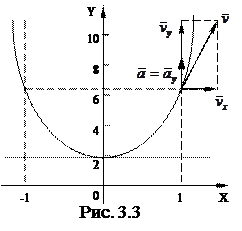
Составляющие скорости показаны на рис. 3.3
 .
.
Вектор скорости 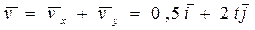 и направлен по касательной к траектории движения точки.
и направлен по касательной к траектории движения точки.
3. Расчет ускорения.
Определим проекции ускорения на оси координат:
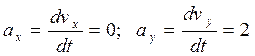 .
.
Модуль ускорения (м/с2)
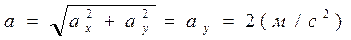
Направляющий косинус и углы, которые вектор ускорения составляет с осями координат:
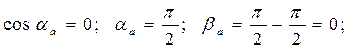 так как
так как 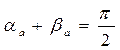 .
.
Вектор ускорения 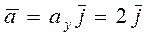 .
.
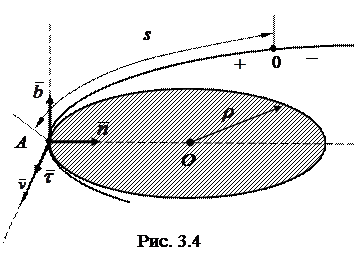 Естественный способ. Этот способ применяют тогда, когда траектория точки известна заранее. Положение точки А определяют дуговой координатой s - расстоянием вдоль траектории от выбранного начала отсчета О (рис. 3.4). При этом произвольно устанавливают положительное направление отсчета координаты s (например, так, как показано на рис.3.4).
Естественный способ. Этот способ применяют тогда, когда траектория точки известна заранее. Положение точки А определяют дуговой координатой s - расстоянием вдоль траектории от выбранного начала отсчета О (рис. 3.4). При этом произвольно устанавливают положительное направление отсчета координаты s (например, так, как показано на рис.3.4).
Движение точки определено, если известны ее траектория, начало отсчета О, положительное направление отсчета дуговой координаты s и закон вижения точки, т. е. зависимость s (t).
Естественные оси координат. Сначала в точке А строится соприкасающаяся окружность, которая из всех мыслимых окружностей, проходящих через точку А, наиболее плотно смыкается с траекторией (рис.3.4). Центр этой окружности О, называется центром кривизны траектории, а ее радиус ρ - радиусом кривизны траектории в точке А. Величина С = 1/ ρ называется кривизной траектории. На пологих участках траектории значения ρ больше, чем в точках искривленных участков. Плоскость, в которой лежит соприкасающаяся окружность, называется соприкасающейся плоскостью, и часть траектории в окрестности точки А практически лежит в этой плоскости.
Естественными осями координат(оси естественного трехгранника)называются три взаимно перпендикулярные оси:
касательная -  к траектории в точке А, направленная в сторону возрастания дуговой координаты s;
к траектории в точке А, направленная в сторону возрастания дуговой координаты s;
главная нормаль - 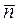 , лежащая в соприкасающейся плоскости и направленная к центру кривизны;
, лежащая в соприкасающейся плоскости и направленная к центру кривизны;
бинормаль -  , перпендикулярная соприкасающейся плоскости и направленная так, что если посмотреть навстречу ее положительному направлению, ближайший поворот от касательной оси к оси главной нормали кажется происходящим против хода часовой стрелки. Единичные векторы (орты) (рис. 3.4) образуют правую тройку. По построению
, перпендикулярная соприкасающейся плоскости и направленная так, что если посмотреть навстречу ее положительному направлению, ближайший поворот от касательной оси к оси главной нормали кажется происходящим против хода часовой стрелки. Единичные векторы (орты) (рис. 3.4) образуют правую тройку. По построению 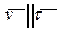 ,
, 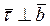 ,
, 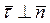 .
.
 Скорость точки. Введем единичный вектор
Скорость точки. Введем единичный вектор 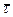 , связанный с движущейся точкой A и направленный по касательной к траектории в сторону возрастания дуговой координаты s (см.рис.3.5). Очевидно, что
, связанный с движущейся точкой A и направленный по касательной к траектории в сторону возрастания дуговой координаты s (см.рис.3.5). Очевидно, что 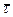 - переменный вектор: он зависит от s. Вектор скорости
- переменный вектор: он зависит от s. Вектор скорости 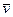 точки A направлен по касательной к траектории, поэтому его можно представить так:
точки A направлен по касательной к траектории, поэтому его можно представить так:
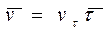 , (3.5)
, (3.5)
где v = ds/dt - проекция вектора 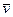 на направление вектора
на направление вектора 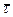 , причем vτ - величина алгебраическая.
, причем vτ - величина алгебраическая.
Кроме того, очевидно, что | vτ |. = |  | = v.
| = v.
Ускорение точки. Продифференцируем (3.5) по времени:
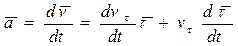 . (3.6)
. (3.6)
Затем преобразуем последний член этого выражения:
 . (3.7)
. (3.7)
Определим приращение вектора 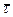 на участке ds (рис. 3.5). Можно строго показать, что отрезок траектории между точками 1и2при стремлении к нулю стремится к дуге окружности с центром в некоторой точке О.
на участке ds (рис. 3.5). Можно строго показать, что отрезок траектории между точками 1и2при стремлении к нулю стремится к дуге окружности с центром в некоторой точке О.
Как видно рис. 3.5, угол 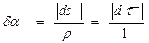 , т.е.
, т.е. 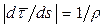 , причем при ds →0
, причем при ds →0  .
.
Введя единичный вектор 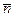 нормали к траектории в точке 1, направленный к центру кривизны, запишем последнее равенство в векторном виде:
нормали к траектории в точке 1, направленный к центру кривизны, запишем последнее равенство в векторном виде:
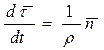 (3.8)
(3.8)
Теперь остается подставить (3.8) в (3.7) и полученное выражение - в (3.6), в результате найдем
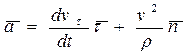 (3.9)
(3.9)
Здесь первое слагаемое называют тангенциальным ускорением 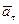 , а второе - нормальным (или центростремительным)
, а второе - нормальным (или центростремительным) 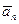 :
:
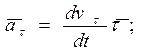
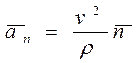 . (3.10)
. (3.10)
Таким образом, полное ускорение 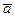 точки может быть представлено как сумма тангенциального
точки может быть представлено как сумма тангенциального 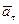 и нормального
и нормального 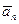 ускорений.
ускорений.
Модуль полного ускорения точки
 .
.
Задача 3.3
Точка движется по плоской траектории так, что ее тангенциальное ускорение aτ = b, а нормальное ускорение an = ct 4, где b и c - положительные постоянные, t - время. В момент t = 0 точка начала двигаться. Найти радиус кривизны ρ траектории 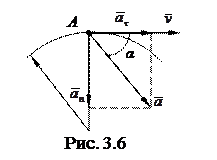 точки и ее полное ускорение a в зависимости от пройденного пути s.
точки и ее полное ускорение a в зависимости от пройденного пути s.
Решение. Элементарное приращение скорости точки dv = aτdt. Проинтегрировав это уравнение, получим v = bt.
Пройденный путь s = bt2/2. Радиус кривизны траектории согласно (3.10) можно представить как 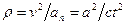 ,
,
или  . Полное ускорение (рис. 3.6)
. Полное ускорение (рис. 3.6)
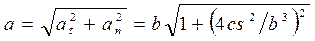 .
.
|
|
|
|
|
Дата добавления: 2014-11-29; Просмотров: 1187; Нарушение авторских прав?; Мы поможем в написании вашей работы!