Двухфакторный дисперсионный анализ

Дисперсионный анализ особенно эффективен при одновременном изучении нескольких факторов. В этом случае при постановке активного эксперимента одновременно варьируют все факторы, и каждое наблюдение выходного параметра Y используют для их одновременной оценки. При этом немаловажен и тот факт, что в ряде случаев можно не делать параллельных наблюдений, ограничиваясь лишь одним наблюдением для каждого сочетания уровней изучаемых факторов.

Пусть требуется изучить одновременное влияние на процесс двух качественных факторов Х_А и Х_В. Фактор Х_А исследуется на уровнях Х_А1, Х_А2, …, Х_Аi, …, Х_АК, фактор Х_В – на уровнях Х_В1, Х_В2, …, Х_Вj, …, Х_Вm. Допустим, что при каждом сочетании уровней исследуемых факторов было проведено по n параллельных наблюдений (равное количество взято для упрощения вкладок). Матрицу наблюдений в рассматриваемом случае можно представить в виде таблице 4.4.

Общее число наблюдений равно

.

Таблица 4.4 – Исходные данные для двухфакторного ДА с равным числом повторений опытов

ХВ	XA
xA 1	xA 2	…	xAi	…	xAK
xB1	y 111, y 112, …, y 11 n	y 211, y212, …, y 21 n	…	yi 11, yi 12, …, yi 1 n	…	yK 11, yK 12, …, yK1n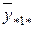
		…		…
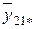
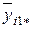
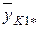
xB2	y 121, y 122, …, y 12 n	y 221, y 222, …, y22n	…	yi 21, yi 22, …, yi 2 n	…	yK 21, yK 22, …, yK 2 n
		…		…
…	…	…	…	…	…	…	…
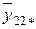
xBj	y 1 j 1, y 1 j 2, …, y 1 jn	y 2 j 1, y 2 j 2, …, y 2 jn	…	yij 1, yij 2, …, yijn	…	yKj 1, yKj 2, …, yKjn
		…		…
…	…	…	…	…	…	…	…
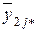
xBm	y 1 m 1, y 1 m 2, …, y 1 mn	y 2 m 1, y 2 m 2, …, y 2 mn	…	yim 1, yim 2, …, yimn	…	yKm 1, yKm 2, …, yKmn
		…		…
			…		…

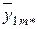
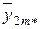
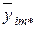
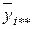
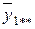
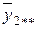
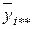
В таблице 4.4. обозначено:

i= 1 ,k – число уровней фактора Х_А (число столбцов);

J= 1 ,m – число уровней фактора Х_В (число строк);

l= 1 ,n – число наблюдений ячейке (число параллельных опытов);

y _111, y ₁₁₂ ,…, y _{11 n},…, у_kmn – наблюдавшиеся значения выходного параметра;

– среднее значение в ячейке;

(4.42)

– среднее значение по уровням фактора Х_В (средние по строкам);

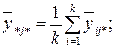(4.43)

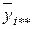– среднее значение по уровням фактора Х_А (средние по столбцам);

(4.44)

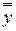– общее среднее;

. (4.45)

Будем полагать, что предпосылки проведения ДА выполнены. В рассматриваемых условиях любое наблюдение из таблицы 4.4 может быть представлено виде следующей модели:

(4.46)

где – общая средняя (математическое ожидание для среднего по всей таблице 4.4);

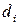– эффект фактора Х_А на i -ом уровне (отклонение математического ожидания выходного параметра при i -ом уровне фактора Х_А от общего математического ожидания);

– эффект фактора Х_В на j -ом уровне (отклонение математического ожидания выходного параметра при j -ом уровне фактора Х_B от общего математического ожидания);

– эффект взаимодействия факторов Х_А и Х_В;

– случайный остаток или вариация результатов внутри отдельной ячейки (ошибка воспроизводимости).

Эффект взаимодействия факторов представляет собой отклонение среднего по наблюдениям в ij -ой серии от суммы первых трех членов модели (4.46). Если предположить, что между факторами нет взаимодействия, то можно построить линейную модель вида:

. (4.47)

Эта модель, как правило, применяется лишь в случае отсутствия параллельных опытов, например, как показано в таблице 4.5. (при анализе трех и более факторов отдельные эффекты взаимодействия удается оценить и без параллельных наблюдений).

Таблица 4.5 – Исходные данные для двухфакторногоДАсодним наблюдением в ячейке

ХВ	XA
xA1	xA2	…	xAi	…	xAK
xB1			…		…
xB2			…		…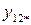
…	…	…	…	…	…	…	…
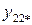
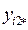
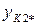
xBj			…		…
…	…	…	…	…	…	…	…
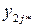
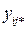
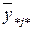
xBm			…		…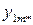
			…		…

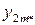
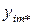
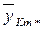
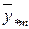
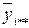
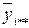
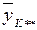
В таблице 4.5 обозначено:

i= 1 ,k – число уровней фактора Х_А (число столбцов);

J= 1 ,m – число уровней фактора Х_В (число строк);

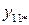,…, у_kmn – наблюдавшиеся значения выходного параметра;

– среднее значение по уровням фактора Х_B (средние по столбцам);

(4.48)

– среднее значение по уровням фактора Х_А (средние по столбцам);

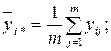(4.49)

– общее среднее;

. (4.50)

В рассматриваемом случае (модель (4.47)) оценки общей дисперсии, как и ранее, можно получить из основного тождества ДА. Однако следует подчеркнуть, что в двухфакторном ДА, в отличие от однофакторного, общая сумма квадратов отклонений наблюдений от общего среднего (числитель (4.9)) раскладывается согласно (4.47) уже не на две, а на три части: часть, обусловленную влиянием фактора Х_А, часть, обусловленную влиянием фактора Х_{В ,} и часть, обусловленную влиянием всех неучтенных факторов.

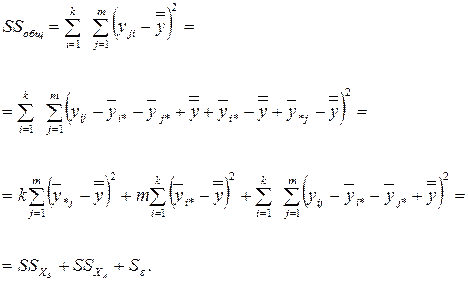(4.51)

Слагаемое представляет собой сумму квадратов разностей между средними по строкам и общим средним и характеризует изменение выходного параметра по фактору Х_B:

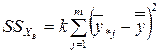. (4.52)

Слагаемое представляет собой сумму квадратов разностей между средними по строкам и общим средним и характеризует изменение выходного параметра по фактору Х_A:

. (4.53)

Слагаемое SS_Е называется остаточной суммой квадратов и характеризует влияние неучтенных моделью (4.47) факторов:

. (4.54)

Зная суммы квадратов отклонений, определим оценки соответствующих дисперсий:

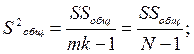(4.55)

(4.56)

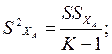(4.57)

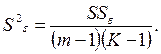(4.58)

Нулевые гипотезы о незначимости факторов Х_А и Х_В проверяют по критерию Фишера. Если дисперсионное отношение

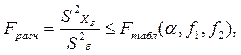(4.59)

где

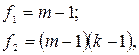
принимается гипотеза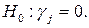

Если дисперсионное отношение

(4.60)

нулевая гипотеза отвергается, и влияние фактора Х_В считается значимым.

Аналогично, если дисперсионное отношение

(4.61)

где

принимается гипотеза При несправедливости неравенства

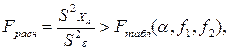(4.62)

влияние фактора Х_А считается значимым. При проверке нулевых гипотез, также принимается односторонний F-критерий (приложение Б).

При проведении ДА в условиях линейной модели (4.47) удобно использовать следующий алгоритм расчета. Находят:

- итоги по столбцам:

;

- итоги по строкам:

;

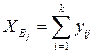- сумму квадратов всех наблюдений:

;

- сумму квадратов итогов по столбцам, деленную на число наблюдений в столбце:

;

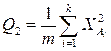- сумму квадратов итогов по строкам, деленную на число наблюдений в строке:

;

- квадрат общего итога, деленный на число всех наблюдений (корректирующий член):

- сумму квадратов для столбца:

;

- сумму квадратов для строки:

;

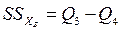- общую сумму квадратов:

- остаточную сумму квадратов:

- оценку дисперсии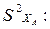

;

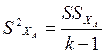- оценку дисперсии

;

- оценку дисперсии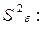

.

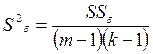Результаты расчета удобно представлять в виде таблицы 4.6.

Таким образом, установив при помощи ДА значимость влияния факторов, выясняют затем, какие именно средние значения Y различны.

Как было отмечено ранее, линейная модель вида (4.47) справедлива лишь при отсутствии взаимодействия факторов. В противном случае этому взаимодействию как самостоятельному фактору присуща своя дисперсия .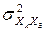

В приведенном выше алгоритме при наличии взаимодействия между факторами Х_А и Х_В дисперсия 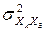, как составная часть, входит в дисперсию ошибки . Выделить и оценить эту дисперсию можно только при наличии параллельных наблюдений (таблица 4.4). При указанном расположении наблюдений их рассеяние в каждой ячейке относительно среднего той же ячейки обусловлено действием только случайных причин с дисперсией 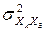. Рассеяние же самих средних в ячейках по всем возможным сочетаниям уровней факторов Х_А и Х_В вокруг общего среднего, помимо фактора случайности, вызывается влиянием фактора взаимодействия Х_А Х_В с дисперсией 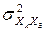. Кроме этих факторов на рассеяние средних по строкам оказывает влияние только один фактор Х_В с дисперсией 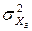, а на рассеяние средних по столбцам – только один фактор Х_А с дисперсией 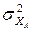, так как все уровни другого фактора в каждом из этих случаев осреднены.

В этом случае для получения модели вида (4.46) общую сумму квадратов отклонений, наблюдений от общего среднего необходимо разложить уже на четыре компонента, отвечающие перечисленным выше факторам.

Таблица 4.6 – Двухфакторный ДА с одним наблюдением в ячейке

Компоненты дисперсии	Число степеней свободы	Сумма квадратов	Средний квадрат (оценка дисперсии)	Математическое ожидание среднего квадрата
ХА	k- 1
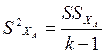
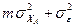
ХВ	m- 1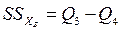
Остаточная (ошибки)	(k- 1 )(m- 1 )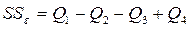
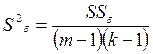
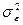
Общая (полная)	km- 1			–

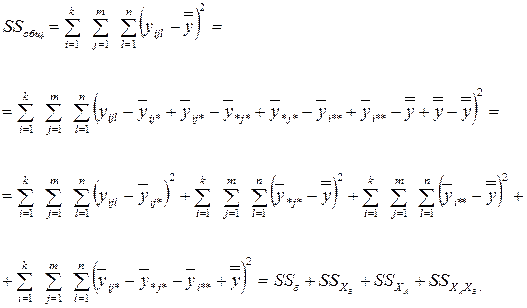(4.63)

Полученные суммы имеют следующий смысл: - сумма квадратов отклонений внутри ячейки (серии опытов), характеризующая рассеяние отдельных наблюдений 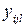в сериях опытов только за счет влияния фактора случайности, так как на протяжении серии опытов внутри одной ячейки факторы Х_А и Х_В остаются неизменными:

, (4.64)

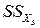– сумма квадратов отклонений между строками:

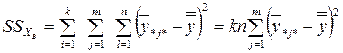. (4.65)

Сумма характеризует рассеяние средних 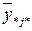по строке в результате действия фактора случайности (с дисперсией среднего для строки 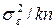) и фактора Х_В (с дисперсией );

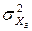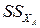– сумма квадратов отклонений между строками:

. (4.66)

Сумма 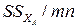характеризует рассеяние средних по столбцам в результате действия фактора случайности (с дисперсией среднего для строки 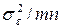) и фактора Х_А (с дисперсией );

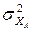– сумма квадратов отклонений между сериями:

(4.67)

Сумма характеризует рассеяние средних по ячейкам (сериям) в результате действия фактора случайности (с дисперсией среднего ячейки ) и фактора взаимодействия (с дисперсией ).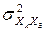

Поделив полученные суммы на соответствующее число степеней свободы, получим оценки дисперсий:

– оценку общей дисперсии по всем N = mkn наблюдением выходного параметра с числом степеней свободы f_общ= mkn- 1 = N - 1:

(4.68)

– оценку дисперсии рассеяния внутри ячеек, то есть оценку остаточной дисперсии, которая является средневзвешенной оценкой дисперсии по всем km сериям наблюдений с числом степеней свободы:

;

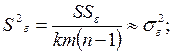(4.69)

– оценку дисперсии рассеяния между строками с числом степеней свободы

(4.70)

– оценку дисперсии рассеяния между столбцами с числом степеней свободы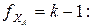

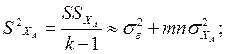(4.71)

– оценку дисперсии рассеяния между сериями (ячейками) с числом степеней свободы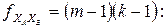

(4.72)

Правильность подсчета чисел степеней свободы можно проверить с помощью соотношения

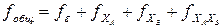. (4.73)

При практических расчетах удобно использовать следующий алгоритм. По таблице 4.4. находят:

– суммы наблюдений в каждой ячейке:

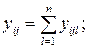
– квадрат суммы в каждой ячейке:

– итоги по столбцам:

– итоги по строкам:

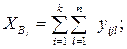
– сумму всех наблюдений (общий итог):

– сумму квадратов всех наблюдений:

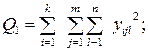
– сумму квадратов итогов по столбцам, деленную на число наблюдений в столбце:

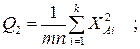
– сумму квадратов итогов по строкам, деленную на число наблюдений в строке:

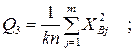
– квадрат общего итога, деленный на число всех наблюдений (корректирующий член):

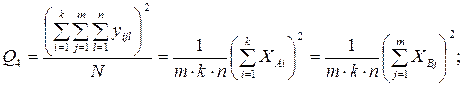
– сумму квадратов для столбца:

;

– сумму квадратов для строки:

;

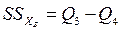– сумму квадратов для дисперсии воспроизводимости:

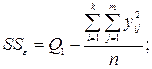
– общую сумму квадратов:

– остаточную сумму квадратов отклонений для эффекта взаимодействия X_AX_B:

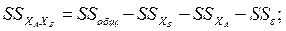
– оценку дисперсии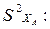

;

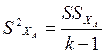– оценку дисперсии

;

– оценку дисперсии

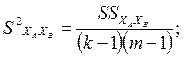
– оценку дисперсии воспроизводимости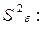

.

Полученные результаты целесообразно представить в виде таблицы 4.7.

Проверка гипотезы о значимости влияния факторов X_A, X_B и взаимодействия X_AX_B производится по критерию Фишера. С этой целью рассчитывают дисперсионное отношение вида:

(4.74)

Таблица 4.7 – Двухфакторный ДА с n наблюдениями в каждой ячейке

Компоненты дисперсии	Число степеней свободы	Сумма квадратов	Средний квадрат (оценка дисперсии)	Математическое ожидание среднего квадрата
ХА	k- 1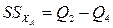
ХВ	m- 1
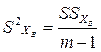
XAXB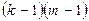
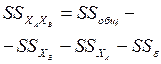
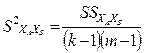
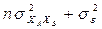
Остаточная (ошибки)	km (n- 1)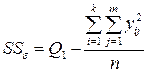
Общая (полная)	kmn- 1		–	–

и сравнивают их с табличными критическими

.

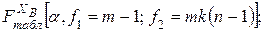
Если дисперсионные отношения (4.74) больше соответствующих табличных, то влияние факторов X_A, X_B и взаимодействия X_AX_B следует признать значимыми. В противном случае – незначимыми. Дальнейший анализ и выводы о существенности влияния факторов производят так же, как и в однофакторном ДА.

Таким образом, мы рассмотрели процедуру двухфакторного дисперсионного анализа. При многофакторном анализе последовательность операций аналогична, но значительно усложняются таблицы наблюдений и расчетные формулы.

С целью упрощения расчетов можно воспользоваться одним из возможных алгоритмов машинной обработки результатов проведения ДА.

Примечания.

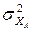1 По своему физическому смыслу символы (смотреть таблицу 4.2), и (смотреть таблицы 4.6 и 4.7) являются сокращенным обозначением следующих функций параметров:

где d_i – эффект фактора Х (Х_А) на i -ом уровне;

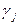– эффект фактора Х_В на j -ом уровне.

Однако по аналогии с обычной дисперсией в большей части литературных источников их называют дисперсиями соответственно факторов Х, X_A и X_B. В этом смысле оценки дисперсией 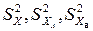(смотреть таблицы 4.2, 4.6 и 4.7) для корректности следует называть средними квадратами.

2 При проведении ДА можно получить математическую модель, но это не является главной целью, так как при наличии качественных факторов эту модель нельзя использовать для прогнозирования выходного параметра, не найденных из эксперимента.

3 Если исследуемый процесс определяется действием, как качественных, так и количественных факторов, то для их исследования следует применить ковариационный анализ, объединяющий регрессионные и дисперсионные методы.

Задача 4.2.

Пусть имеется три однотипные боевые машины реактивных систем залпового огня (БМ РСЗО) (при постоянных уровня фактора Х_В), заряженные снарядами М21 ОФ, которые были произведены на двух различных заводах (два уровня фактора Х_А). Стоит задача: по результатам стрельб, представленных в таблице 4.8, оценить существенность влияния факторов X_A и X_B на величину систематического отклонения неуправляемых реактивных снарядов от точки прицеливания по дальности ().

Таблица 4.8

Уровни фактора ХВ (j=1,m)	Уровни фактора XA (i=1,k)
xA1	xA2
xB1	190,.260,170,170,170 (l=I,n)	190,150,210,150,150
xB2	150,250,220,140,180	230,190,200,190,200
xB3	190,185,135,195,195	150,170,150,170,180

Будем считать, что все предпосылки проведения дисперсионного анализа (ДА) выполняются.

Дата добавления: 2014-11-29