Число степеней свободы

Стандартное (среднеквадратическое) отклонение

Степень разнообразия особей в группе по изучаемому признаку измеряется несколькими показателями, из которых наибольшее значение имеет стандартное отклонение или стандартное отклонение:

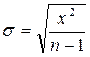(7.1)

(7.2)

s – стандартное отклонение;

x² – сумма квадратов центральных отклонений, т. е. квадратов разностей между каждым значением и средней арифметической;

X_i – значение признака у каждого объекта в группе;

μ – средняя арифметическая признака для данной группы;

n – 1 – число степеней свободы, равное числу объектов в группе без одного.

Число степеней свободы равно числу элементов свободного разнообразия в группе. Оно равно числу всех имеющихся элементов изучения без числа ограничений разнообразия.

Например, для исследования требуется взять три объекта с любым развитием изучаемого признака. В данном случае величина признака не имеет никаких ограничений, поэтому число степеней свободы n= 3 – 0 = 3.

Если требуется взять три числа с условием, что сумма их должна быть равна определенной величине, например: 100, то первое число может быть любой величины: 80, 800 и т. д., второе число также может быть выбрано свободно без всяких ограничений, например 10, 1269 и т. д., то третье же число может иметь только одно значение, такое, чтобы оно вместе с двумя предыдущими составило бы в сумме 100. Если два первых числа были 80 и 10, то третье должно быть 10; если два первых числа 800 и 1269, то третье должно быть отрицательным: –1969 (800+1269–1969 = 100).

В данном случае, при одном ограничении (сумма чисел должна быть равна 100), два числа выбираются свободно, а третье не имеет свободы выбора: для трех чисел имеются две степени свободы
n = 3 – 1 = 2.

Для n значений при k ограничениях имеется n = n–k степеней свободы.

При вычислении средней арифметической никаких ограничений величины значений признака не имеется. Поэтому число элементов, образующих среднюю арифметическую, равно числу вариантов.

При вычислении среднего квадратического отклонения имеется одно ограничение. Сигма вычисляется для определенной группы, имеющей определенную среднюю арифметическую. Поэтому разнообразие элементов, образующих стандартное отклонение, ограничено этим одним условием и в данном случае число степеней свободы равно числу вариантов без одного n = n–1.

Определение критерия достоверности разности 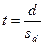двух средних величин производится при числе степеней свободы
n = n₁+n₂–2. Это связано с тем, что ошибка разности определяется на основе ошибок 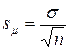обеих средних, каждая из которых имеет число степеней свободы (для соответствующей сигмы) n–1. В сумме число степеней свободы:

n = n₁–1+n₂–1 = n₁+n₂–2

Для критерия достоверности разности двух коэффициентов корреляции число степеней свободы равно для первого коэффициента n₁ = n₁–2; для второго коэффициента n₂ = n₂–2; для их разности:

n_d = n₁+n₂ = n₁–2+n₂–2 = n₁+n₂–4

По приведенным формулам можно рассчитывать стандартное отклонение для групп любого объема.

Стандартное отклонение служит основным показателем разнообразия значений признака в группе. Используется сигма и как самостоятельный показатель, и как основа для построения многих других показателей статистики: коэффициента вариации, ошибок репрезентативности, различных показателей распределения, коэффициентов корреляции и регрессии, элементов дисперсионного анализа, формул регрессии.

Основное свойство всякой группы – разнообразие входящих в нее объектов по изучаемому признаку – измеряется несколькими показателями. К ним относятся: лимиты и размах, стандартное отклонение, коэффициент вариации, квартили, децили, перцентили.

Следует иметь в виду, что формула сигмы с числом степеней свободы в знаменателе подкоренного количества применяется только для выборок:

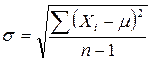(7.3)

Сигма генеральной совокупности вычисляется по формуле:

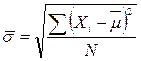, (7.4)

где:

– генеральная сигма;

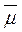– генеральная средняя;

N – объем генеральной совокупности

Пример

На сельскохозяйственной выставке сравниваются экспонаты двух хозяйств, представивших лучшие экземпляры тыквы со своих огородов. Первое хозяйство представило 6 тыкв, весивших 33, 37, 32, 38, 34, 36 кг, второе представило 5 тыкв, весивших 33, 37, 34, 36, 35 кг.

Так как средний вес экспонатов оказался одинаковым у обоих экспонатов (μ₁ = 35, μ₂ = 35), было решено провести сравнение стандартности тыкв по среднему стандартному отклонению.

В данном случае сравнивались не выборки, а генеральные совокупности, так как оценка проводилась по выставочным экземплярам, которые целиком исчерпывали всю требующуюся в данном случае информацию.

Дисперсии и средние стандартные отклонения (сигмы):

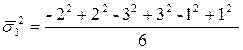
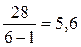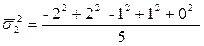
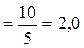(а не );

(а не ).

;

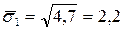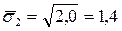
Коэффициенты вариации:

; .

Оказалось, что второй совхоз представил более стандартную партию тыкв.

Так как сравнение в данном случае проводилось по генеральным параметрам, то разность сигм заведомо достоверна и не нуждается в определении достоверности. Обычные методы определения достоверности разности в данном случае не нужны и неприменимы, так как сравниваемые группы выбирались не так, как это требуется при организации выборок (не рендомизированно).

Сравнение стандартности двух партий тыкв характеризует более благоприятно второе хозяйство, которое смогло подобрать более выровненную группу экспонатов.

Дата добавления: 2014-11-29