Достоверность различия распределений

Кумулята

Кумулята – это изображение распределения в виде кривой, ординаты которой пропорциональны накопленным частотам вариационного ряда. Чтобы составить ряд накопленных частот, нужно к частоте первого, наименьшего класса, прибавить частоту второго класса (S f₂ для второго класса), затем прибавить частоту третьего класса (S f₃ для третьего класса) и т. д. Кумулята для распределений веса показана на рисунке 8.3. Кумулята иногда имеет преимущество перед вариационной кривой.

Рисунок 8.3 – Кумулята

Некоторые методы математической статистики основаны на использовании кумуляты. К ним относятся, например, критерий лямбда и χ², определяющие достоверность различия двух распределений.

Статистическая гипотеза – это определённое предположение о распределении вероятностей, лежащем в основе наблюдаемой выборки данных.

Проверка статистической гипотезы – это процесс принятия решения о том, противоречит ли рассматриваемая статистическая гипотеза наблюдаемой выборке данных.

Статистический тест или статистический критерий – строгое математическое правило, по которому принимается или отвергается статистическая гипотеза.

Наряду с нулевой гипотезой, которая принимается или отвергается по результату анализа выборки, статистические критерии могут опираться на дополнительные предположения, которые априори предполагаются выполненными.

Параметрические критерии предполагают, что выборка порождена распределением из заданного параметрического семейства. В частности, существует много критериев, предназначенных для анализа выборок из нормального распределения. Преимущество этих критериев в том, что они более мощные. Гипотезы о виде распределения проверяются с помощью критериев согласия.

Не всегда эмпирическое распределение хорошо соответствует нормальному. Для практических и научных работ часто требуется выяснить, сильно или слабо расходятся эмпирический и теоретический ряды. Для этого необходимо установить такой предел, недостижение которого означает, что расхождение между эмпирическим и нормальным распределениями еще не настолько велико, чтобы с ним считаться, и что данный эмпирический ряд еще можно практически принять за нормальный. Для этой цели применяются особые показатели, из которых в биологических исследованиях используются критерий χ² и критерий λ.

8.4.1 Критерий χ² (хи квадрат)

Критерий χ² предложен Карлом Пирсоном и применяется во всех случаях, когда необходимо определить степень отличия фактического распределения частот от теоретического. Определяется величина χ² по следующей формуле:

(8.1)

тде f – эмпирическая частота; – теоретическая частота.

Современные способы, использования критерия χ² отличаются от тех, которые были предложены автором критерия, и тех его модификаций, которые были разработаны в первой половине двадцатого века.

Критерий χ², или критерий согласия (подобия), используется для оценки степени соответствия эмпирических данных определенным теоретическим предпосылкам, нулевой гипотезе (Н_о).

Гипотеза опровергается, если χ²_факт ≥ χ²_теор, и не опровергается, если χ²_факт < χ²_теор. Когда фактические и теоретически ожидаемые частоты полностью совпадают, χ² = 0.

Следует обратить внимание на то, что при определении различий между эмпирическим и теоретическим распределениями требуется обратный порядок планирования порогов вероятности безошибочных прогнозов.

В таких исследованиях чем выше ответственность, тем при меньшем расхождении распределений различие уже считается достоверным, и, наоборот, чем менее ответственно исследование, тем при большем расхождении распределений различие между ними все еще может считаться недостоверным.

Это различие в планировании порогов достоверности показано в таблице 8.2.

Таблица 8.2 – Три порога вероятности безошибочных прогнозов

Пороги	Минимальная вероятность безошибочных прогнозов	Ответственность исследований
В обычных биологических работах	При анализе расхождений эмпирических и теоретических распределений
I	β1=0,95	Обычная	Повышенная
II	β2=0,99	Повышенная	Обычная
III	β3=0,999	Высокая	Пониженная

Таким образом, при оценке различий между эмпирическими и теоретическими распределениями в большинстве биологических работ следует устанавливать не первый, а второй порог вероятности.

Первый порог (β₁ ≥ 0,95) будет излишне строгим для обычных биологических работ, но для очень ответственных исследований придется устанавливать эту пограничную вероятность и даже еще меньшую, например β ≥ 0,93, β ≥ 0,90.

Равнение на третий порог (β₃ ≥ 0,999) можно допускать только в первых ориентировочных наблюдениях, так как при таком пороге нормальными распределениями будут считаться такие, которые уже сильно от него отличаются.

Еще одно важное отличие, касающееся минимально допустимых теоретических частот в крайних классах распределения, которые следует объединять в один общий крайний класс.

После того как будет найдено эмпирическое значение χ², надо произвести его оценку путем сравнения со стандартными значениями этого критерия для числа степени свободы ν₂ = r₂ – 3 и трех порогов вероятности безошибочных прогнозов.

При определении числа степеней свободы в нормальном распределении данных по классам следует помнить, что в данном случае (нормальное распределение) имеются три ограничения: определенный объем всей группы (n), определенная средняя (μ), от которой берутся центральные отклонения, и определенная сигма (σ), по которой производится нормирование центральных отклонений средин классов.

Поэтому число степеней устанавливается следующим образом.

1 Определяется первое число степеней свободы, равное имеющемуся числу классов без трех: ν₁ = r₁ – 3

2 По первому числу степеней свободы устанавливается минимально допустимая теоретическая частота крайних классов.

3 Классы с малыми (меньше минимально допустимых) теоретическими частотами объединяются в один общий крайний класс; при этом получается второе, уменьшенное число классов: r₂.

4 Устанавливается окончательное число степеней свободы, равное уменьшенному числу классов без трех: ν₂ = r₂ – 3.

8.4.2 Критерий λ (лямбда)

Критерий λ предложен советскими учеными
А. Н. Колмогоровым и Н. В. Смирновым и может применяться для определения достоверности расхождения между фактическими и теоретическими распределениями, а также различий между любыми двумя распределениями частот одного и того же признака даже в том случае, когда число классов и число данных у этих распределений неодинаково. Для применения критерия лямбда не требуется определять число степеней свободы и не нужны таблицы для определения трех стандартных значений критерия, так для любого числа классов эти предельные значения одинаковы: 1,36 1,63; 1,95 и соответствуют обычным трем степеням вероятности достоверного различия: β₁ = 0,95; β₂ = 0,99; β₂ = 0,999. Единственным условие применения критерия лямбда является достаточная численность сравниваемых распределений – не менее нескольких десятков данных.

Для сравнения эмпирического распределения с теоретическим при одинаковом числе классов и при одинаковой общей численности групп критерий лямбда определяется по формуле:

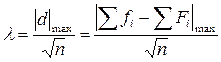(8.2)

где |d|_max – максимальная разность (без учета ее знака) между накопленными частотами в эмпирическом и теоретическом распределениях для одного и того же класса;

n – общее число данных, образовавших эмпирическое распределение.

Для определения критерия лямбда требуется составить ряды накопленных частот для обоих сравниваемых распределени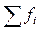й и 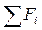, взять наибольшую разность (без учета ее знака) между этими величинами и полученную разность разделить на .

Эмпирический критерий оценивается по трем постоянным стандартным значениям: 1,36 – 1,63 – 1,95. При этом применяется такой же обратный порядок порогов достоверности расхождения, как и при использовании критерия χ².

Для выяснения достоверности различия между двумя любыми распределениями частот одного и того же признака при неодинаковом числе данных и классов критерий лямбда вычисляется по формуле:

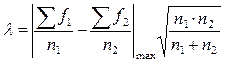(8.3)

– суммы накопленных частот по каждому классу первого распределения (начиная с меньшего), деленные на общее число данных;

– то же по второму распределению;

– максимальное абсолютное значение (без учета знака) разности частных от деления накопленных частот на численности групп по каждому классу, начиная с наименьшего;

n₁, n₂ – общее число данных по первому и второму распределениям.

Дата добавления: 2014-11-29