Свойства операций

Свойства операций

1^о .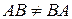

Проверим это свойство для матриц 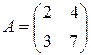и .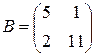

, .

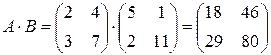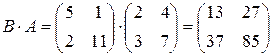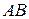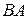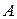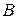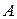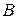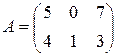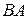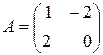На самом деле может случиться так, что произведение существует, а не существует (это связано с тем, что операция умножения матриц и определена только для того случая, когда число столбцов матрицы равно числу строк матрицы ). Например, матрицу можно умножить на , а найти произведение – невозможно. Однако, в частном случае равенство возможно, например, для матриц и 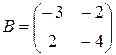. (Поверьте).

2^о .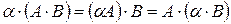

3^о .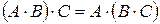

4^о .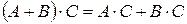

5^о .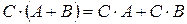

6^о .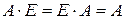

5) Если в матрице 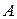поменять местами строки и столбцы, то новая матрица 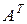называется транспонированной по отношению к матрице :

; .

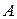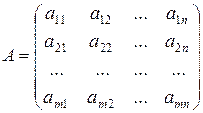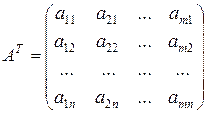Пример 2.5. Для матрицы 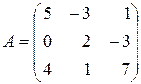запишите соответствующую ей транспонированную.

Решение. Поменяем местами строки и столбцы

.

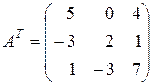1^о 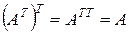, т.е. если над матрицей 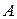дважды произвести операцию транспонирования, то матрица останется неизменной.

Пример 2.6. На примере матрицы 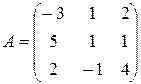, доказать, что .

Решение. Найдем матрицу 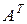, транспонированную по отношению к матрице :

.

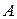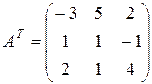После транспонирования последней матрицы, получим:

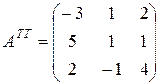, а это в точности есть матрица .

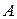2^о 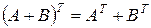, т.е. транспонированная матрица суммы двух матриц равна сумме транспонированных матриц.

Пример 2. 7. Проверим это свойство для матриц и .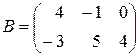

Решение.

Найдем матрицы, транспонированные по отношению к данным

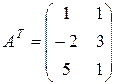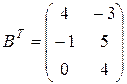; и их сумму .

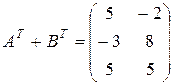Для того, чтобы проверить свойство 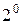, вычислим сумму исходных матриц, а затем транспонируем ее:

, .

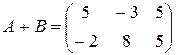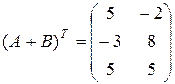Матрицы 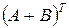и 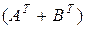равны, что и требовалось доказать.

3^о 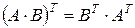, т.е. транспонированная матрица произведения двух матриц равна произведению транспонированных матриц, взятых в обратном порядке.

Пример 2.8. Проверим это свойство для матриц 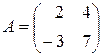и .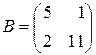

Решение.

Найдем произведение данных матриц:

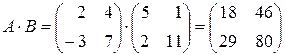
и запишем матрицу, транспонированную по отношению к ней:

.

Найдем произведение матриц, транспонированных по отношению к данным:

, , .

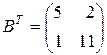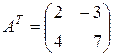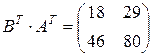Из полученного видно, что: .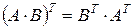

Дата добавления: 2014-11-29