Приклад застосування алгоритму АЗП по дугах, що виходять

ЗАДАЧА ПРО НАЙКОРОТШИЙ ШЛЯХ

Етап. Планування кроку 1.

Зазвичай відомо, у якому стані система може перебувати на початку кроку 1. Тому ніяких припущень про це не треба робити (рис. 6). Враховуючи те, що всі останні кроки вже умовно сплановані, управління на кроці 1 обирається таким чином, щоб воно було оптимальним з урахуванням всіх подальших управлінь.

Рис. 6

Динамічне програмування вирішує задачу, розбиваючи її на підзадачі й поєднуючи їх розв’язки, при цьому воно застосовується тоді, коли підзадачі не є незалежними, тобто, коли у підзадач є спільні «підпідзадачі». Алгоритм, заснований на динамічному програмуванні, розв’язує кожну з підзадач один раз і запам'ятовує відповіді в спеціальній таблиці. Це дозволяє не обчислювати заново відповідь підзадачі, що вже зустрічалася [3].

Обчислення на мережах характерні для ДП. Дослідження мережевих моделей дозволяє краще усвідомити специфіку (суть) обчислювальної схеми ДП.

Кожен багатокроковий процес прийняття рішень може бути зведений до задачі знаходження найкоротшого шляху (ЗЗНШ) у спрямованій ациклічній слоїстій мережі (САСМ). Саме з такої точки зору і будемо розглядати ЗЗНШ.

Розглянемо ряд визначень.

Спрямована мережа - це трійка 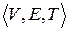, де - непорожня кінцева множина вершин (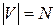), - множина дуг: .

Наявність дуги вказує на можливість прямого руху з вершини до вершини 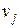. З того, що , не випливає, що . Тому ці дуги називають спрямованими (орієнтованими).

Кожній дузі поставлено у відповідність деяке дійсне число - довжина дуги, що з'єднує вершини і , , .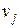

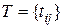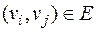Шляхом називається кінцева послідовність вершин, таких, що . Довжина шляху – сума довжин дуг, що входять у нього.

Шлях, у якого , називається циклом.

Мережа називається ациклічною, якщо вона не містить жодного циклу.

В спрямованій ациклічній мережі завжди можна позначити вершини цілими числами від 1 до , таким чином, що для кожної дуги буде справедлива нерівність . Далі будемо вважати, що така нумерація проведена.

Спрямовану ациклічну мережу будемо називати слоїстою, якщо всі її вершини можуть бути розбиті на підмножин (слоїв), що взємно не перетинаються 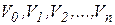, таким чином, що кожна дуга може зв'язувати лише вершини із сусідніх слоїв. Тобто, якщо й , то .

Відзначимо, що в загальному випадку 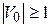й 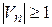, і має сенс розв’язувати задачі при кількості слоїв 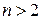(рис. 7).

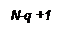
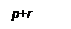
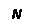
Рис. 7

Кожна спрямована ациклічна мережа може бути зведена до слоїстої мережі шляхом введення фіктивних вершин і дуг. Наступний приклад ілюструє цей процес. Нехай маємо спрямовану ациклічну мережу (рис. 8). Ця мережа не є слоїстою.

Рис. 8

Після додавання фіктивних вершин 4', 5', 6', 7' і 8', а також дуг з нульовими вагами, що входять у ці вершини, одержали слоїсту мережу (рис 9).

Рис. 9

Розглянемо задачу знаходження найкоротшого шляху в САСМ з погляду ідей і прийомів ДП.

Нехай . Мета задачі – знайти найкоротший шлях між вершинами 1 і .

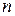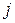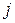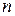Задача може бути інтерпретована як багатокрокова (багатоетапна). У ній кожен шлях складається рівно з дуг - кроків. Під -м кроком (етапом) будемо розуміти перехід зі слою до слою . Таким чином, при переході з вершини 1 у вершину буде зроблено рівно кроків.

На початку кроку 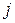система може перебувати в одній з вершин . У цьому випадку кажуть, що система перебуває в одному з можливих станів . Для кожної вершини відомі дуги, що з'єднують її з однією з вершин множини . Інакше кажучи, для кожного стану відомі варіанти розв’язків (управлінь), що переводять систему в один із станів наступного кроку. Таким чином, варіантами розв’язків для стану : є всі дуги (s,k), що починаються в вершині .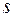

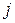Нехай - довжина найкоротшого шляху на кроках від до 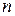включно, за умови, що на початку кроку 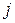система перебуває в стані 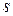. Якщо на кроці 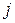, перебуваючи у вершині 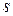, ми приймаємо рішення піти по дузі , то мінімальна довжина шляху з вершини 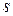в цьому випадку становитиме

де – довжина найкоротшого шляху від вершини 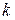до вершини , що складається з кроків 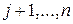. Перебравши всі можливі варіанти розв’язків і знайшовши мінімум, отримаємо:

(1)

Цей вираз справедливий і при , якщо прийняти .

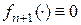З урахуванням позначень, мета нашої задачі – знайти .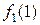

3.1 Схема алгоритму зворотньої прогонки (АЗП) по дугах, що виходять

1. Вважаємо, що .

2. Планування кроку .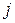

2.1. Виділити всі можливі стани, які можуть бути на початку кроку 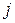, тобто визначити множину .

2.2. Для кожного знайти умовне оптимальне управління:

(мінімум шукаємо по дугах, що виходять).

Запам'ятати вершину , при якій досягається мінімум у виразі .

3. , якщо , то перейти до п. 4, інакше - перейти до п. 2.

4. Формування оптимального розв’язку. Для знаходження найкоротшого шляху пройти по мережі в напрямку, зворотньому до напрямку розрахунків, використовуючи знайдені умовні оптимальні розв’язки (вершини) .

Використовуючи алгоритм зворотньої прогонки по дугах, що виходять, знайти найкоротший шлях з вершини 1 у вершину 10 (рис. 10).

При застосуванні алгоритму зворотньої прогонки, першим планується крок 4 (останній крок). Вважаємо, що 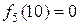(довжина найкоротшого шляху від вершини 10 до самої себе).

Планування кроку 4. Виділимо всі можливі стани, які можуть мати місце на початку кроку 4, тобто визначимо множину : . Для цих вершин знайдемо умовні оптимальні розв’язки й відповідно, де – довжина найкоротшого шляху на кроці 4 (на кроках від 4-го до (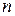 = 4)-го включно), за умови, що на початку кроку 4 система перебуває в стані (вершині) 8. Аналогічно визначається . Відповідно до виразу (1) отримаємо:

; ;

; .

!	У цьому випадку, з кожної вершини виходить тільки по одній дузі (говоримо, що в кожному стані можливий тільки один варіант розв’язку). Тобто маємо “вибір без вибору”. Така ситуація завжди має місце, якщо в останньому слої є тільки одна вершина (у нас - вершина 10).

Заповнюємо таблицю таким чином:

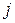
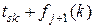
Крок	Можливі стани на початку кроку (вершини )	Варіанти розв’язків	Вартість розв’язку	Умовний оптимальний розв’язок
Вихідна дуга	Наступна вершина
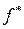
		r		1+0=1	10
		s		4+0=4		4

У стовпчику 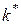вказується вершина 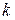, перехід у яку з вершини 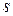забезпечує мінімум виразу (1). У стовпчику f^* вказується значення цього мінімуму – довжина найкоротшого шляху з вершини 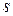до останньої вершини 10.

Планування кроку 3. На початку цього кроку система може перебувати в одному з трьох станів (вершин): 5, 6 й 7. Якщо система, наприклад, перебуває в стані (вершині) 5, то з нього можна вийти по дугах 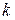і (і потрапимо у вершини 8 або 9 відповідно). Тоді для стану 5 умовний оптимальний розв’язок знаходиться таким чином:

,

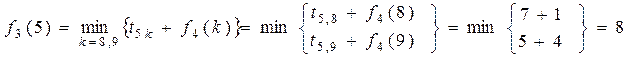– тобто, якщо з вершини 5 перейти у вершину 8, то досягається мінімум виразу (1).

!	Згадаємо одне з основних положень ДП: „ в процесі поетапного планування управління на кожному кроці повинно обиратися з урахуванням його майбутніх наслідків ”. У нашому випадку це здійснюється через урахування величин і .

Для стану 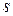= 5 таблицю заповнюємо таким чином:

		k		7+1=8
l		5+4=9

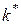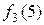Отримали: = 8, = 8.

Аналогічні дії виконуються і для випадків, коли на початку кроку 3 система перебуває в станах 6 або 7:

, .

, .

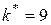		m		3+1=4
n		4+4=8
	p		7+1=8
q		1+4=5

Аналогічно плануються кроки 2 і 1.

Повний процес розв’язку задачі наведено у таблиці 1:

Таблиця 1

Крок	Можливі стани на початку кроку (вершини )	В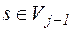аріанти розв’язків	Вартість розв’язку	Умовний оптимальний розв’язок
Вихідна дуга	Наступна вершина
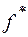
		r		1+0=1	10
	9	s		4+0=4
		k		7+1=8
		l		5+4=9
		m		3+1=4
		n		4+4=8
	7	p		7+1=8
		q		1+4=5
		d		10+8=18
		e		12+4=16
		f		5+8=13
	3	g		10+4=14
		h		7+5=12
		i		15+4=19
		j		13+5=18
		a		2 + 16=18
	1	b		5 + 12=17	3
		c		3 +18=21

Порядок формування відповіді (найкоротшого шляху) показаний стрілками.

Відповідь: найкоротший шлях: 1-3-7-9-10, довжина шляху 17.

Дата добавления: 2014-11-29