Приклад 3.1

Приложения

Приложение 1.

Таблица П1. Средние технологические нагрузки (относительные)

Месяц	Годовое время использования максимума технологической нагрузки
4300-4600	4700-5000	5000-5300
	0,92	0,95	0,97
	0,81	0,89	0,92
	0,65	0,76	0,77
	0,59	0,67	0,68
	0,57	0,61	0,64
	0,55	0,59	0,63
	0,56	0,61	0,65
	0,63	0,67	0,71
	0,75	0,78	0,83
	0,88	0,89	0,91
	0,95	0,96	0,97

Приложение 2.

Таблица П2. Укрупненные показатели максимального теплового потока на отопление жилых зданий (5 этажей и более) 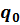, Вт/м²

Расчетная температура для отопления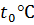^,	-5	-10	-15	-20	-25	-30	-35	-40	-45	-50	-55
Здания, постройки до 1985 года
Здания, постройки после 1985 года

Приложение 3.

Таблица П3. Укрупненные показатели среднего теплового потока на горячее водоснабжение жилых и общественных зданий при температуре воды 55°С 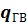, Вт/чел.

Средняя за отопительный период норма расхода горячей воды на одного человека в сутки	л/сут	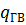, Вт/чел
В жилых домах с душами без ванн
В жилых домах с сидячими ваннами и душами.
В жилых домах с душами и ваннами длиной 1,5 – 1,7 м
В жилых домах с высотой более 12 этажей, с повышенными требованиями к благоустройству

Приложение 4

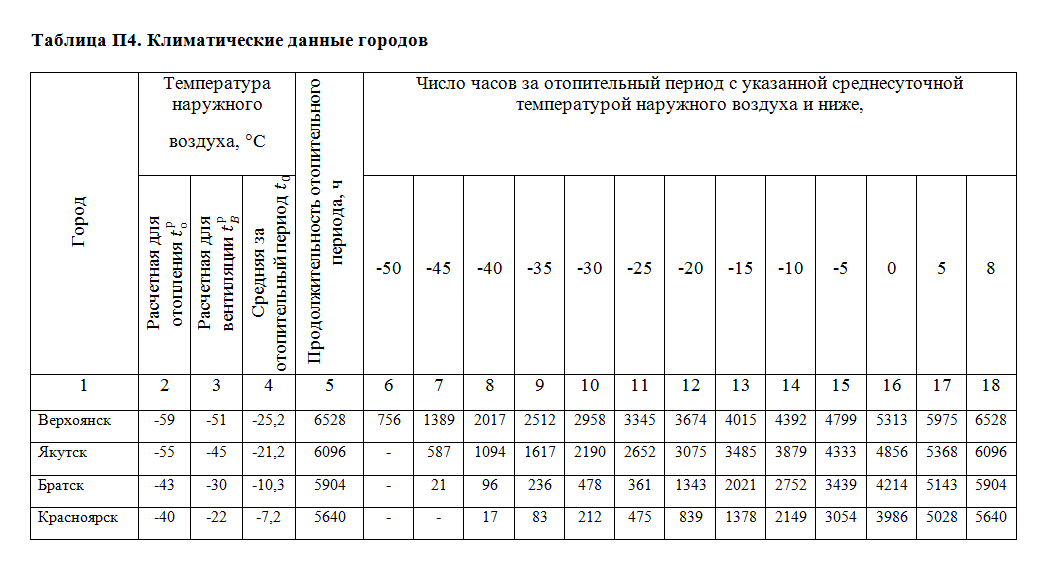
Продолжение приложения 4

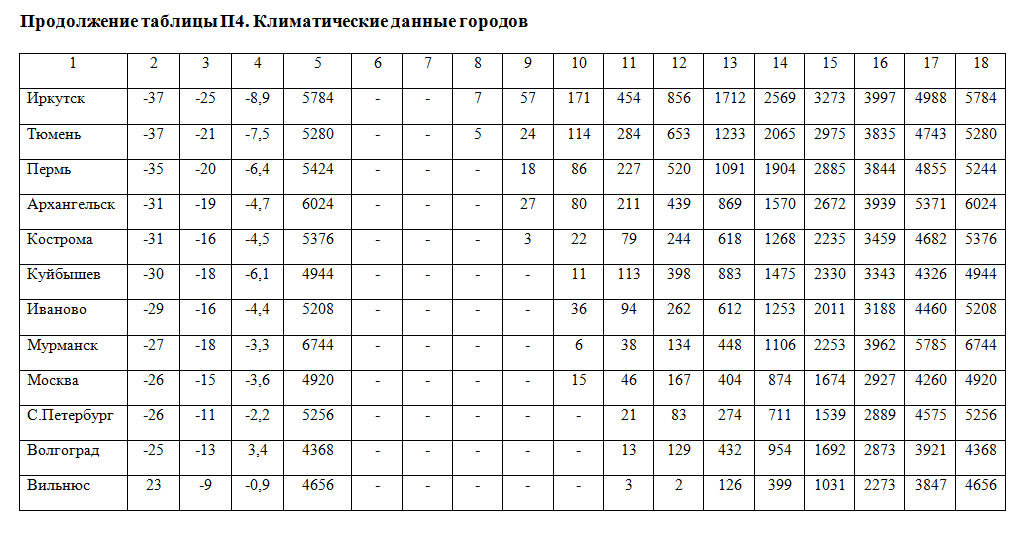
Окончание приложения 4

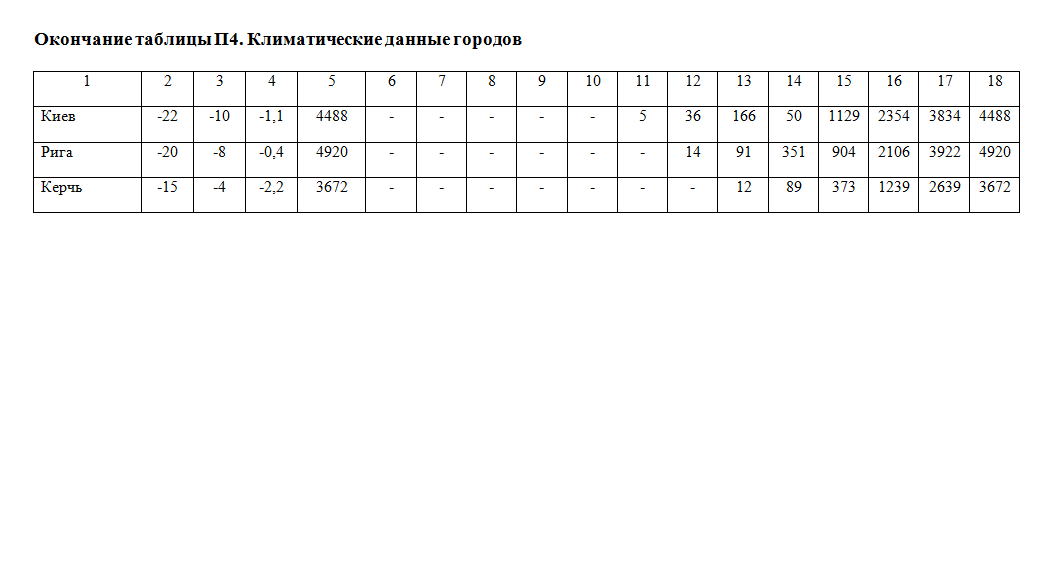
Приложение 5

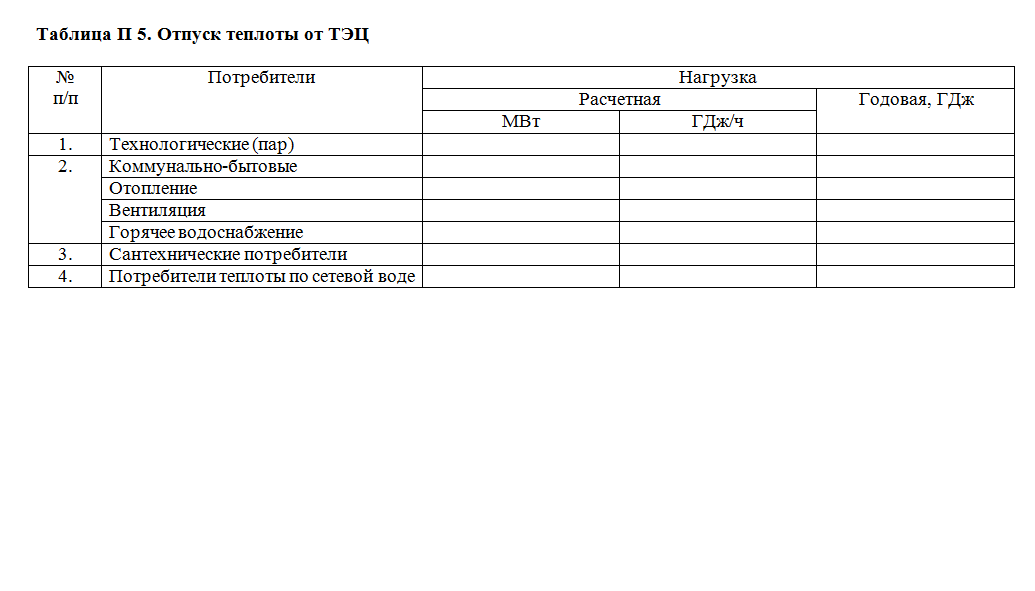
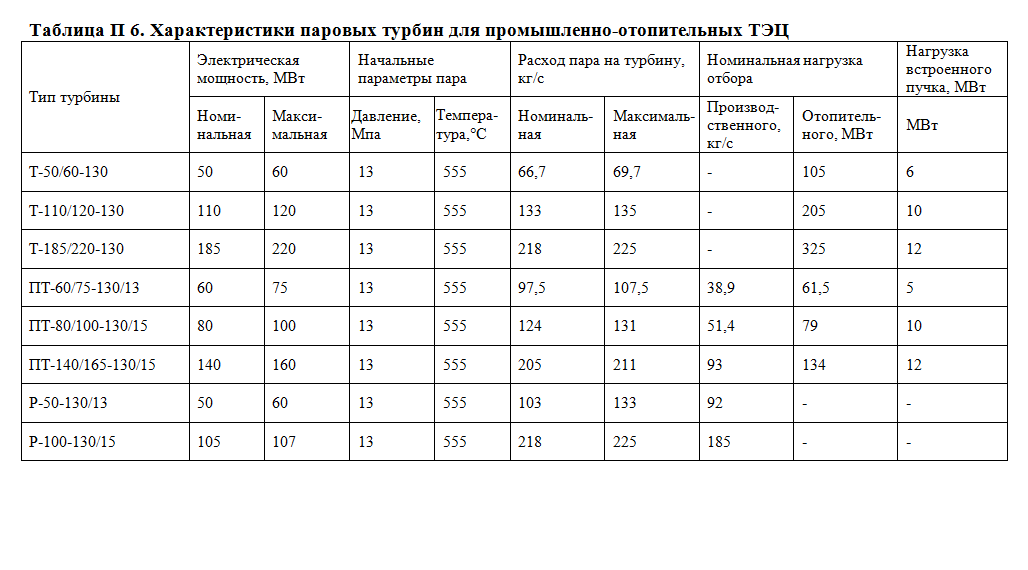
Приложение 6

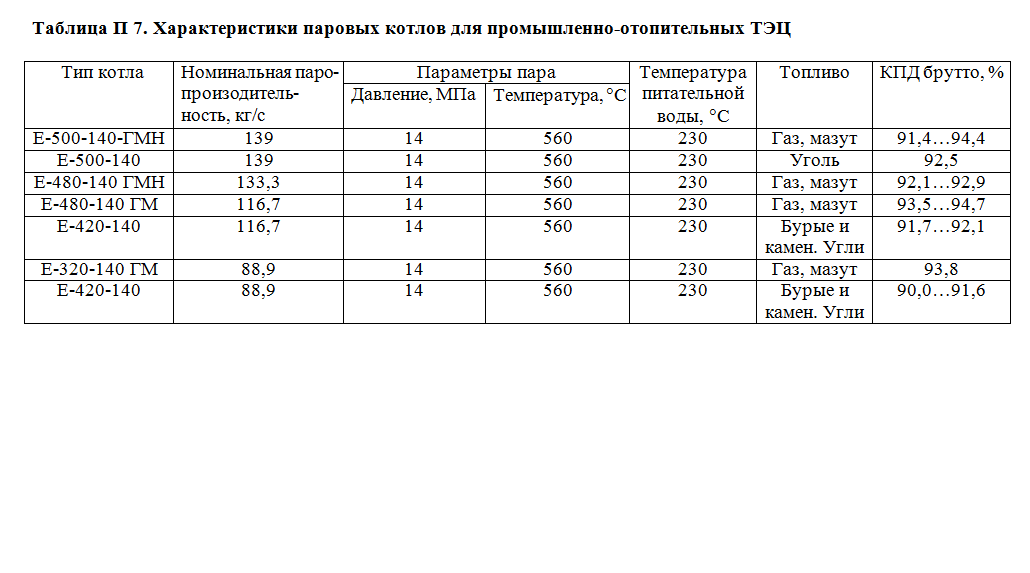
Приложение 7

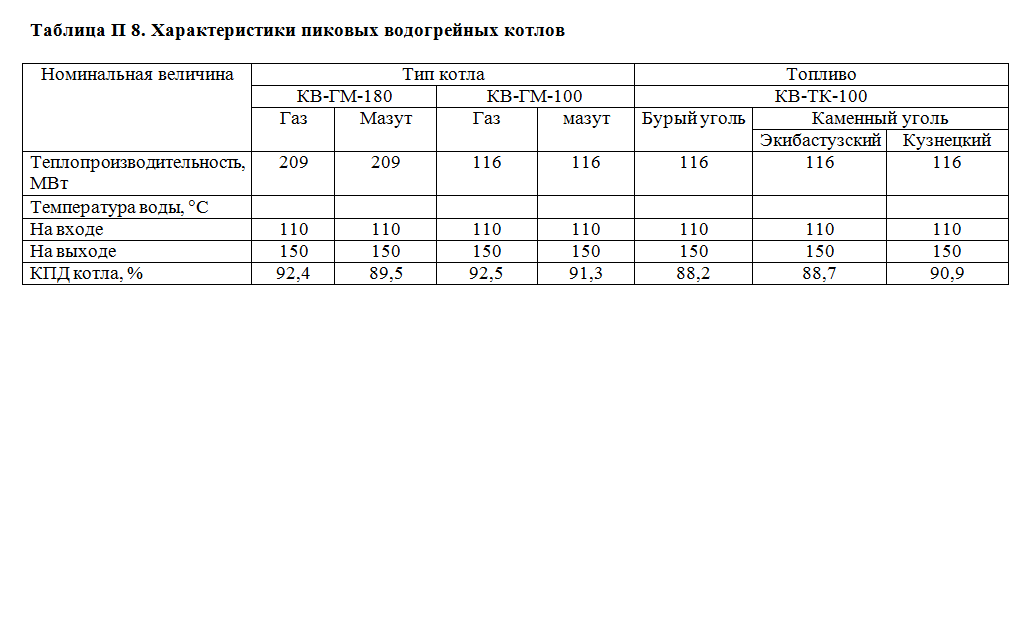
Приложение 8

Приложение 9

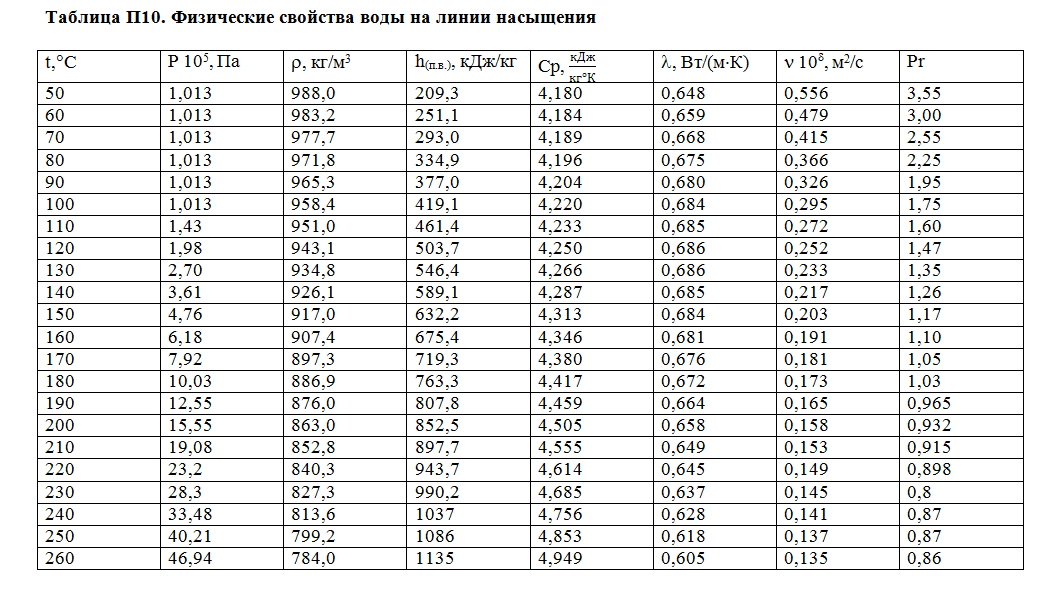
Приложение 10

Окончание приложения 10

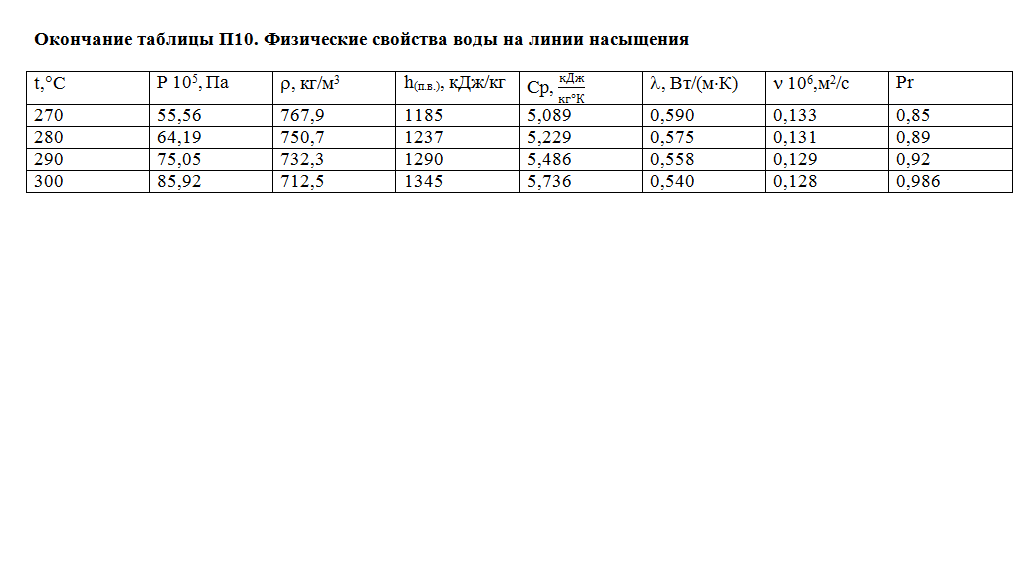
Приложение 11

Приложение 12

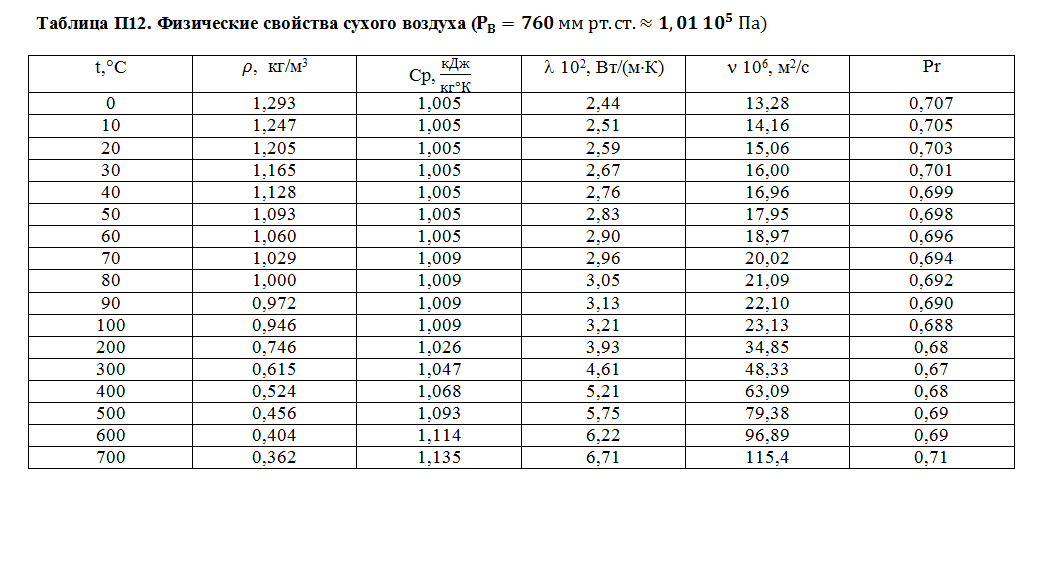
Приложение 13

Учебное издание

Языкова Любовь Николаевна

МЕТОДИЧЕСКИЕ УКАЗАНИЯ

К ПРАКТИЧЕСКИМ ЗАНЯТИЯМ

по ОБЩЕЙ ЭНЕРГЕТИКЕ

Редактор Г.В. Казьмина

Подписано в печать________________. Формат 60х84 1\16. Бумага офсетная.

Объем 3 п.л. Тираж 50 экз. Заказ № ________. Ризография.

Издательство Липецкого государственного технического университета

Полиграфическое подразделение издательства ЛГТУ

398600 Липецк, ул. Московская, 30.

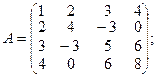
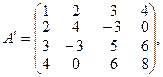
тобто A = A¢.

Неважко показати, що A′A=AA′ — симетричні матриці.

Зауважимо, що справджується тотожність

(A′)′ = A.

3.2. Елементарні дії над матрицями

Дві матриці A = (a_ij) та B = (b_ij) одного й того самого порядку (m × n) вважаються рівними, якщо всі відповідні елементи цих матриць рівні між собою, тобто

A = B <=> a_ij = b_ij (i = 1, …, m; j = 1, …, n)

Отже, матриці різних порядків завжди не рівні між собою.

матриці можна додавати, віднімати, множити матрицю на число та матриці на матрицю.

Додавання і віднімання виконуються лише для матриць одного й того самого порядку. Якщо A = (a_ij) і B = (b_ij) мають порядок m × n, то

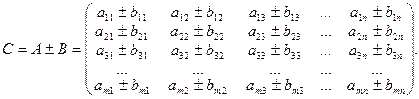(3.10)

Скорочено: C = (c_ij) =(a_ij ± b_ij).

Очевидно,що

A+B=B+A; (A+B)′= A ′+ B ′; A +(B-A)= B

При додаванні матриць А, В, і С одного й того самого порядку справджується закон асоціативності:

(А + В) + С = А + (В + С).

Добутком скаляра l на матрицю 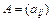порядку (m × n) називається матриця, елементи якої дорівнюють l a_ij, тобто

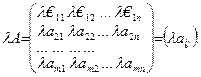(3.10)

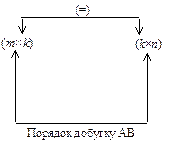Рис. 3.1

При множенні матриці А на скаляр l виконуються такі закони:

а) λA=Aλ;

б) (λA)′ = λA′;

в) λ(A + B)= λA+ λB;

г) (λ+γ)A= λA+γA;

д) (λγ)A= γ(λA);

Дві матриці А і В можна помножити одна на одну, тобто визначити С = АВ, коли кількість стовпців матриці А дорівнює кількості рядків матриці В.

Нехай маємо матрицю А порядку m × k і матрицю В — k × n. Добуток двох матриць С = АВ існує, бо матриця А має k стовпців, і стільки ж рядків має матриця В. Матриця-добуток С = АВ матиме порядок m × n, тобто стільки рядків, скільки має перша матриця А, і стільки стовпців — скільки їх має матриця В. Цей висновок унаочнює рис. 3.1.

Правило множення двох матриць А на В: кожний елемент матриці c_ij є сумою добутків відповідних елементів i -го рядка матриці А на елементи j -го стовпця матриці В, тобто

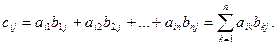
Приклад. Знайти добуток С = АВ, коли

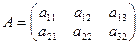— порядок 2 × 3;

— порядок 3 × 2.

Добуток цих двох матриць існує, оскільки кількість стовпців матриці А дорівнює трьом, стільки ж рядків має матриця В, тобто виконується умова множення двох матриць. Перемноживши ці матриці, дістанемо:

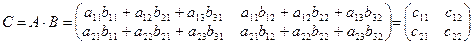(3.11)

Порядок матриці С, яка є добутком А і В, дорівнює 2 × 2.

При множенні матриць діють такі закони:

а) AB≠BA, тобто добуток матриць не є комутативним.

Нехай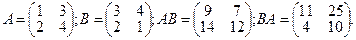

Отже, .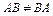

б) (АВ) С = А (ВС);

в) (А+В) С = АС + ВС;

г) С (А+В) = СА + СВ;

д) α (AB) = (αA) B=A (αB);

е) АE = EA = A, де E — одинична матриця того самого порядку, що й матриця А;

є) (AB)′ = B ′ A ′;

ж) (ABC)′ = C′B ′ A ′.

Як окремий випадок добуток матриці розміру 1 × p (вектор-рядок) на матрицю порядку p × 1 (вектор-стовпець) дає скаляр, а саме:

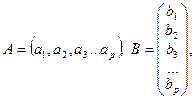
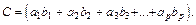
Якщо вектор ,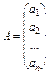

то

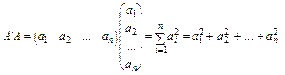
і

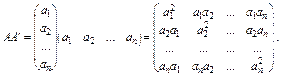
Означення 3.11. Два вектори А і В, для яких скалярний добуток дорівнює нулю і A′A≠0, B′B≠0, називаються взаємно ортогональними, тобто A′B= 0 або B′A =0 .

Нехай ; 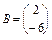, тоді 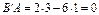, отже, вектори А і В — взаємно ортогональні.

Означення 3.12. Квадратна матриця А, яка задовольняє умову A ² =A (A ² =A∙A), тобто квадратна матриця, яка при множенні сама на себе не змінюється, називається ідемпотентною.

Нехай 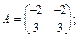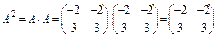, тобто A ² =A, матриця А є ідемпотентною.

3.3. Скалярні характеристики матриць

Кожна матриця А має скалярну характеристику, яка називається рангом матриці А (rg A). Крім неї, квадратні матриці мають ще дві скалярні характеристики: слід матриці А (tr A) і її детермінант, або визначник, який позначають (det A або ). Значення всіх трьох характеристик пов’язане з конкретною матрицею.

Розглянемо докладніше ці характеристики.

Для визначення рангу матриці введемо поняття лінійної комбінації векторів і їх лінійної залежності (незалежності). Для n векторів 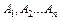лінійна комбінація векторів визначається як , де — дійсні числа.

Означення 3.13. Якщо вектор А подається у вигляді

A = 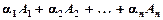, (3.12)

де 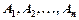— вектори одного й того самого простору, то говорять, що вектор А є лінійною комбінацією векторів 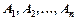. Числа 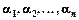називаються коефіцієнтами лінійної комбінації.

Означення 3.14. Вектори 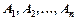n-вимірного простору називаються лінійно незалежними, якщо

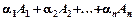= 0 (нуль-вектор), (3.13)

Дата добавления: 2014-11-29