Визначення блочних матриць 1 страница

Коли

= 0,

тобто в разі лінійної незалежності векторів нульовий вектор 0 (0,0,...0) має вигляд тривіальноїлінійноїкомбінаціі векторів .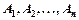

Означення 3.15. Вектори лінійно залежні, якщо існує хоча б одне в лінійній комбінації (3.13) нульового вектора.

Іншими словами, в разі лінійної залежності векторів нуль-вектор не можна подати у вигляді тривіальної лінійної комбінації векторів 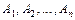, тобто

,

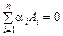коли 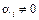хоча б для одного і.

Означення 3.16. Максимальна кількість лінійно незалежних векторів-стовпців (рядків) матриці А називається рангом стовпців (рядків) цієї матриці.

Коли ранг стовпців збігається з рангом рядків матриці А, то можна говорити просто про ранг матриці А.

Зрозуміло, що

rg A 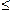min(m,n),

де m — кількість рядків матриці А; n — кількість її стовпців.

Говорять, що матриця А має повний ранг, коли

rg A = min(m,n).

Означення 3.17. Квадратна матриця повного (неповного) рангу називається відповідно невиродженою (виродженою) або регулярною (сингулярною) матрицею.

Прикладом невиродженої матриці є одинична матриця 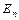(n -го порядку), ранг якої дорівнює n, тобто

rg 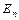= n.

Для рангу виконуються такі співвідношення:

а) rgA = rg ;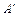

б) rg A = rgA;

в) rgAB 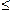min(rgA, rgB).

Означення 3.18. Слідом матриці А порядку n є сума елементів її го­ловної діагоналі, тобто

tr A = .

Для сліду виконуються такі співвідношення:

а)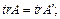

б) де А і В — квадратні матриці одного й того самого порядку; і — дійсні числа;

в) tr(AB) = tr(BA).

Якщо А — симетрична матриця, то

г)

д)

Означення 3.19. Детермінантом (визначником) квадратної матриці А порядку n називається алгебраїчна сума n членів, кожний з яких містить n співмножників, узятих по одному з кожного рядка (стовпця) матриці.

Позначається:

det A або 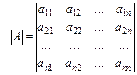(3.14)

Властивості визначників.

1. При транспонуванні матриці її визначник не змінюється, тобто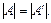

2. Якщо всі елементи рядка (стовпця) матриці дорівнюють нулю, то її визначник також дорівнює нулю.

3. При перестановці двох будь-яких стовпців (рядків) визначника його знак змінюється на протилежний, а абсолютна величина не змінюється.

4. Визначник з двома однаковими стовпцями (рядками) дорівнює нулю.

5. При множенні якого-небудь стовпця (рядка) на довільне число 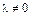значення визначника множиться на це саме число.

6. Спільний множник всіх елементів стовця (рядка) можна винести за знак визначника.

7. Якщо два стовпці (рядки) визначника пропорційні, то визначник дорівнює нулю.

8. Визначник не зміниться, якщо до будь-якого стовпця (рядка) додати елементи другого стовпця (рядка), попередньо помноживши їх на відмінний від нуля множник.

Розглянемо визначник матриці n -го порядку

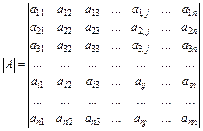(3.15)

Викреслимо в ньому i -й рядок і j -й стовпець, на перетині яких міститься елемент a_ij. У результаті залишиться визначник матриці (n – 1)-го порядку

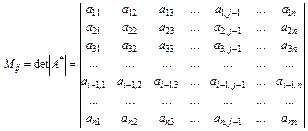. (3.16)

Означення 3.20. Визначник матриці (n – 1) -го порядку, в якій викреслені і-й рядок та j-й стовпець, називається міноромелемента a_ij і позначається .

Мінор , який береться зі знаком (– 1) ^{i + j} (і — номер рядка; j — номер стовпця елемента a_ij), є алгебраїчним доповненням цього елемента, тобто

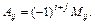
Визначник дорівнює сумі попарних добутків елементів будь-якого його стовпця (рядка) на відповідні їх алгебраїчні доповнення:

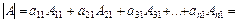
(3.17)

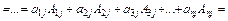
Ця властивість дає змогу розкласти визначник за елементами стовпця (рядка). Нехай потрібно знайти визначник . Розкладемо його за елементами другого рядка:

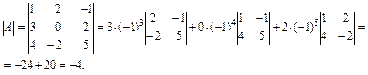
Зауважимо, що детермінант другого порядку обчислюють відніманням добутку елементів побічної від добутку елементів головної діагоналі:

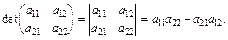
Обчислити детермінант матриці А розміром 3 × 3 можна згідно з властивістю (18) або за правилом Сарруса (Sarrus):

+ + + – – –

– – – + + +

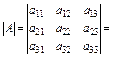
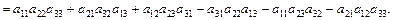
Визначимо за правилом Сарруса:

Правило Сарруса часто називають правилом трикутника. Далі поступово проілюструємо обчислення всіх членів визначника .

Члени зі знаком «плюс»:

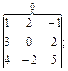
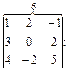
Члени зі знаком «мінус»:

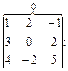
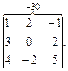
Користуючись поняттям детермінанта, дамо інше означення рангу матриці.

Означення 3.21. Рангом матриці А називається найвищий порядок відмінного від нуля мінора цієї матриці.

Якщо rg A = r, то це означає, що серед мінорів матриці є, зрештою, хоча б один мінор r -го порядку, відмінний від нуля, тоді коли всі мінори вищого порядку: r + 1, r + 2 і т.д. дорівнюють нулю.

Нехай потрібно знайти ранг матриці А:

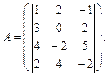
Згідно з означенням рангу матриці його значення не може перевищувати 3.

Обчислимо один з визначників третього порядку матриці А:

Отже, ранг матриці А дорівнює 3.

3.4. Обернена матриця.
Обернення (інвертування) матриць

Поняття оберненої матриці є одним з центральних у матричних перетвореннях. Дамо означення оберненої матриці та розглянемо її знаходження.

Означення 3.22. Для кожної невиродженої матриці А порядку n × n існує однозначновизначена обернена матриця 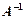того самого порядку, така що виконується рівність

(3.18)

— одинична матриця порядку n.

Отже, умова невиродженості (несингулярності) матриці А є необхідною і достатньою для існування оберненої матриці . Процес знаходження називають інвертуванням матриці А

А інвертування

Таким чином, інвертуватись можуть тільки квадратні матриці, визначник яких відмінний від нуля.

Теорема 3.1. Якщо визначник (det А) не дорівнює нулю, то матриця А має обернену:

(3.19)

де — визначник матриці А; J — так звана приєднана до А матриця. Вона складається з алгебраїчних доповнень 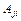до елементів 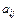матриці А, а саме:

Отже,

(3.20)

Наведемо основні властивості оберненої матриці:

а) ;

б) ;

в) ;

г) ;

д) ;

е) .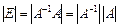

Дамо означення ще одного типу матриць. якщо матрицю називають ортогональною.

Приклад 3.2. Знайти матрицю обернену до матриці А:

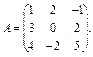
(див. підрозд. 3.3).

Визначимо приєднану матрицю J:

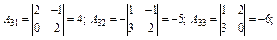
Отже,

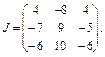
Тоді

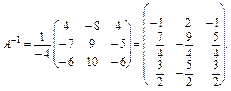
Перевіримо, чи справді матриця є оберненою до матриці А. Знайдемо або ; у результаті має бути одинична матрицю Е. Отже, перевіряється рівність = = E:

3.5. Блочні матриці.
Дії з блочними матрицями

В цілому ряді випадків доцільно великі матриці розбивати вертикальними і горизонтальними прямими на кілька частин. Наприклад, нехай матриця А має порядок 5×6:

(3.21)

(3.21)

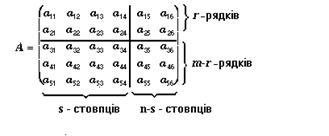
Розіб’ємо її на чотири підматриці:

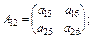
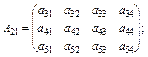
Тоді матрицю А запишемо:

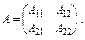(3.22)

Таким чином, маємо два різні записи однієї і тієї ж матриці А. В (3.22) матриця А складається з блоків елементів, або підматриць, тому таку матрицю часто називають блочною. Розбиття матриці роблять так, щоб підматриці, які стоять поруч ( – ; – 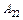), мали б рівну кількість рядків (відповідно r; m – r), а підматриці, які розміщені одна під одною ( – ; – ), — рівну кількість стовпців, а саме: s; n – s (3.21).

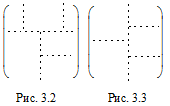
Неприпустимі такі розбиття матриць, схеми яких показані на рис. 3.2 і 3.3.

3.5.2. Дії з блочними матрицями

а) Додавання матриць.

Нехай маємо блочні матриці А i B одного і того ж порядку та однаково розбиті:

Матриця 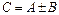є також блочною матрицею того ж порядку, що й матриці А i B:

(3.23)

Таким чином, при додаванні (відніманні) блочних матриць насамперед має виконуватись умова, що відповідні матриці-доданки мають однаковий порядок.

Зауважимо, якщо матриці розбиті таким чином, що можна виконати дію подібно тому, як це зроблено при додаванні матриць А i B в (3.23), то таке розбиття має назву «відповідне».

б) Множення матриць.

Нехай А — матриця порядку m × k; a B — матриця порядку k × n. У такому разі існує добуток С = АВ (див. рис.3.1). Нехай матрицю А розбито на дві підматриці:

(3.25)

(3.24)

(3.24)

Другу матрицю В розбито на дві підматриці , :

(3.25)

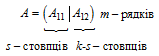
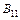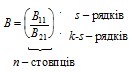
Добуток двох матриць є матриця ,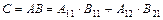

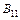де має порядок m × s; – s × n;

– m × (k – s); – (k – s) × n.

Нехай матриці А i B розбито відповідно на чотири підматриці:

Тоді відповідні підматриці мають розміри:

– r × s; – (m – r) × s;

– r × (k – s); – (m – r) × (k – s);

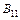– s × p; – (k – s) × p;

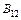– s × (n – p); – (k – s) × (n – p).

Добуток С = АВ складається з чотирьох підматриць C ₁₁, C ₁₂, C ₂₁, C ₂₂:

Розміри підматриць відповідно дорівнюють:

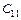– r × p; – r × (n – p);

– (m – r) × p; – (m – r) × (n – p).

Отже, при множенні блочних матриць має існувати відповідність між кількістю стовпців першої матриці А і кількістю рядків другої матриці В, тобто вони мають бути рівними.

Далі з блочними матрицями виконують операцію множення за тими самими правилами, що й зі звичайними матрицями.

Приклад 3.3. Знайти добуток С = АВ двох блочних матриць А i B:

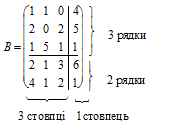
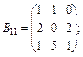
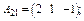
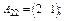
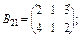
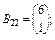
Обчислюємо добуток С = АВ:

;

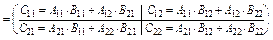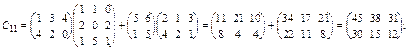
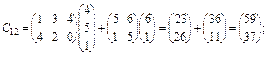
Запишемо блочну матрицю-добуток С = АВ:

(3.26)

(3.26)

Отже, блочна матриця С = АВ має стільки рядків, скільки їх має блочна матриця А (m = 3), і стільки стовпців, скільки їх має блочна матриця В (n = 4).

Існує поняття прямого, або кронеккерового, добутку двох матриць. Якщо матриця А має порядок m × n, а матриця В — розмір p × q, то їх прямий добуток позначається і обчислюється так:

Порядок матриці є mp × nq.

Приклад 3.4. Знайти прямий добуток , якщо:

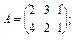
А має порядок 2 × 3; В — порядок 2 × 2; — порядок 4 × 6.

Якщо матриці А та B квадратні й невироджені, а також мають один і той самий розмір, то справджується властивість: (на відміну від .

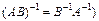Для блочної матриці

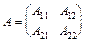
існує таке правило транспонування:

;

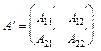множення блочної матриці на число виконується так:

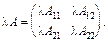
3.6. Обернення блочних матриць (формула Фробеніуса).
Детермінант блочної матриці

Нехай А — невироджена матриця, яка є блочною

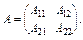
Обернена до А матриця — також блочна, причому

, (3.27)

де ;

Вираз (3.27) відомий в літературі як формула Фробеніуса. Для оберненої матриці виконується рівність: , де Е — одинична підматриця.

Запам’ятайте такий вираз:

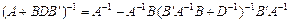, (3.28)

де А i D — невироджені матриці відповідно розміру m × n i n × n; матриця В — порядку m × n.

Детермінант (визначник) квадратної блочної матриці А визначається як

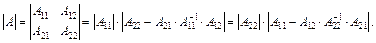(3.29)

Нехай матриця А — невироджена і має блочно-діагональний вигляд:

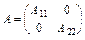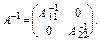, (3.30)

Визначник такої блочної матриці:

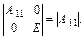
Визначник блочно-діагональних матриць:

(3.31)

і

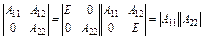. (3.32)

3.7. Системи лінійних рівнянь

Запишемо систему рівнянь у матричному вигляді

АХ = В, (3.32)

де

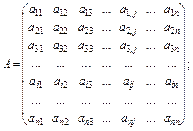
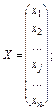
Матриця А є квадратною порядку n; вектор-стовпець Х має розмір n × 1; вектор-стовпець В — порядок n × 1.

Якщо матриця А невироджена, тобто rgA = n і 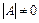, то система лінійних рівнянь (3.32) має єдиний розв’язок виду

(3.33)

Приклад 3.5. Знайти розв’язок системи

У матричному виді:

AX = B;

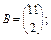
отже,

.

= –2 – 15 = –17 — матриця невироджена.

Запам’ятайте: для матриці обернена матриця має вигляд .

.

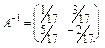Дата добавления: 2014-11-29