Квадратична форма та її властивості

Квадратична функція n змінних називається квадратичною формою і може бути подана у вигляді:

,

де , , ,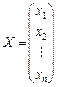

причому матриця С завжди симетрична, тобто c_ij=c_ji для всіх .

Квадратична форма Z (X) називається від’ємно означеною, якщо для всіх Х, крім Х = 0, значення Z (X) < 0 (якщо Z (X) ≤ 0, то маємо від’ємно напівозначену квадратичну форму), у протилежному разі Z (X) є додатно означеною (якщо Z (X) ≥ 0, то маємо додатно напівозначену квадратичну форму).

Квадратична форма Z (X) називається неозначеною, якщо вона додатна для одних значень Х і від’ємна для інших.

Вид квадратичної форми можна визначити, використовуючи

— вектор характеристичних коренів (власних значень) матриці С.

Вектор характеристичних коренів матриці С є вектором, кожна компонента якого задовольняє систему рівнянь виду . Система має ненульовий розв’язок, якщо 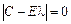. Таке рівняння називається характеристичним рівнянням матриці С і має 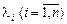коренів, які утворюють вектор :

.

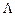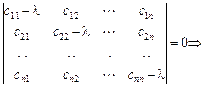
Наведемо без доведення теорему (доведення можна знайти в літературі [19]).

Теорема 8.5. Для того, щоб довільна квадратична форма була додатно (від’ємно) означеною, необхідно і достатньо, щоб усі компоненти вектора характеристичних коренів були додатними (від’ємними) значеннями.

Якщо хоча б один із характеристичних коренів дорівнює нулю, то квадратична форма є напівдодатною (напіввід'ємною). Якщо корені мають різні знаки, то квадратична форма є неозначеною.

Визначити вид квадратичної форми:

Матриця С має вигляд:

.

Запишемо характеристичне рівняння .

Звідси маємо:

.

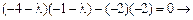
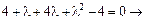
Коренями отриманого квадратного рівняння є: , тоді . Отже, квадратична форма за теоремою 8.5 є напіввід’ємною.

8.8.2. Метод розв’язування задач квадратичного
програмування

Зазначимо, що відомим з теорії аналізу функцій є таке твердження: від’ємно означена квадратична форма є угнутою, а додат­но означена — опуклою.

Розглянемо випадок від’ємно означеної квадратичної форми, що входить у цільову функцію задачі квадратичного програмування.

max , (8.42)

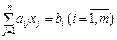; (8.43)

. (8.44)

Оскільки цільова функція задачі є опуклою, а обмеження — лінійні, тобто визначають опуклу множину допустимих розв’язків, то ця задача належить до задач опуклого програмування, для яких справджується твердження, що будь-який локальний максимум є і глобальним. Отже, використовуючи умови теореми Куна — Таккера для задачі (8.42)—(8.44), отримаємо необхідні та достатні умови оптимальності плану у вигляді такої теореми.

Теорема 8.6. Вектор Х ^* є оптимальним розв’язком задачі квадратичного програмування тоді, і тільки тоді, коли існують такі m -вимірні вектори 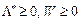і n -вимірний вектор , що виконуються умови:

(І) 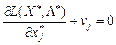, 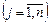; (8.45)

(ІІ) , 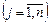; (8.46)

(ІІІ) 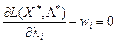, 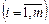; (8.47)

(ІV) 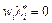, 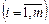. (8.48)

Доведення. Запишемо функцію Лагранжа для задачі квадратич­ного програмування (8.42)—(8.44):

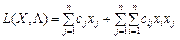+ . (8.49)

Нехай 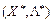— сідлова точка функції Лагранжа, тобто яка визначає оптимальний план задачі квадратичного програмування. Застосуємо теорему 8.4 до виразу (8.49). За теоремою для того, щоб точка 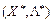визначала оптимальний план, необхідно і достатньо виконання умов (8.38)—(8.41):

для має виконуватись умова:

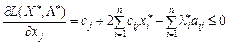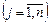, , (8.50)

а також 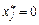, (8.51)

а для 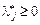має виконуватись умова:

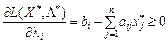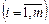, , (8.52)

а також 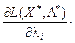. (8.53)

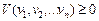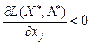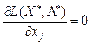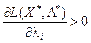Візьмемо два вектори та , компоненти яких будуть введені як додаткові змінні в рівняння (8.50) та (8.52). Для цього виберемо v_j >0, якщо і v_j =0, якщо . Аналогічно виберемо , якщо і 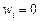, якщо 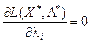. Тепер додамо компоненти вектора 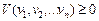у (8.50) і віднімемо компоненти век­тора від (8.52). Враховуючи правила вибору компонент векторів, матимемо для (8.50):

, .

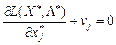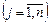Звідси: , тому для (8.51) маємо:

.

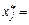
Аналогічно для другої групи обмежень:

, .

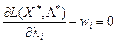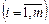Звідки , тому .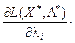

Теорему доведено.

Наведену теорему можна використати для побудови ефективного методу розв’язування задач квадратичного програмування на основі алгоритму симплексного методу.

Умови (8.45)—(8.49) утворюють стосовно змінних X^*, Λ ^*,V,W систему (n + m) рівнянь з 2(n + m) невідомими.

Умови (8.47) та (8.48) означають, що змінні x_j^*, v_j не можуть одночасно мати додатні значення, тобто входити в базис разом. Якщо деякі k компонент вектора X^* додатні, то відповідні їм компоненти вектора V дорівнюють нулю і лише (n – k) компонент відмінні від нуля (додатні). Отже, разом x_j^*, v_j будуть мати не більш ніж n додатних компонент. З аналогічних міркувань щодо рівності (8.48) випливає, що разом з 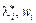буде n + m відмінних від нуля компонент, тобто це може бути базисний розв’язок системи, що утворена умовами (8.45) та (8.47). Для знаходження такого розв’язку можна застосувати симплексний метод.

Якщо зазначена система рівнянь має допустимий план (він буде єдиним), то оптимальний план відповідної задачі квадратич­ного програмування також існує.

Розв’язуємо систему рівнянь (8.45) і (8.47) симплексним методом. Як відомо, спочатку необхідно привести систему обмежень до канонічного виду введенням потрібної кількості додаткових та штучних змінних. Для зведення системи до канонічної форми та визначення початкового опорного плану вводимо штучні змінні α(α₁,α₂,…,α_n) у рівняння виду (8.45), які будуть базисними для першого опорного плану, а змінні 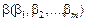— у групу рівнянь (8.47), які також дають базисні змінні для початкового плану. Потім для знаходження базисного розв’язку системи (8.45), (8.47) розв’язуємо симплексним методом таку задачу лінійного програмування:

max (8.54)

за умов:

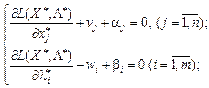(8.55)

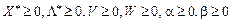. (8.56)

Якщо в процесі розв’язування задачі (8.54)—(8.56) всі штучні змінні будуть виведені з базису (α=0, β=0) і разом з цим для знайдених значень змінних X^*, Λ ^*,V,W виконуються умови (8.46), (8.48), то знайдений розв’язок є оптимальним планом задачі квадратичного програмування (8.42)—(8.44).

Розв’язати задачу квадратичного програмування:

max F =9 x ₁+5 x ₂−2 x ₁²−2 x ₂²−2 x ₁ x ₂

за умов:

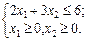
Розв’язання. Оскільки цільова функція виражена сумою лінійної функції F ₁=9 x ₁+5 x ₂ та квадратичної форми F ₂=−2 x ₁²−2 x ₂²−2 x ₁ x ₂, а система обмежень є лінійною, то маємо задачу квадратичного програмування.

Визначимо вид квадратичної форми F ₂=−2 x ₁²−2 x ₂²−2 x ₁ x ₂, для чого відшукаємо корені характеристичного рівняння, що відповідає матриці, складеній з коефіцієнтів при змінних даної функції:

.

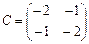Характеристичним рівнянням для матриці С буде:

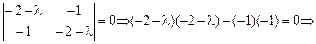
Оскільки обидва корені характеристичного рівняння від’ємні, то квадратична форма F ₂=−2 x ₁²−2 x ₂²−2 x ₁ x ₂ є від’ємно означеною, а отже, опуклою.

Запишемо функцію Лагранжа для цієї задачі:

.

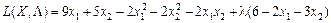Скористаємося теоремою 8.4. Необхідні умови існування екст­ремуму матимуть вигляд:

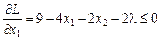, причому ;

, причому ;

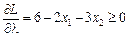, причому ,

де 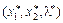— координати сідлової точки.

Обмеження, що відповідають нерівностям, запишемо у вигляді:

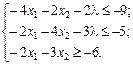
Вводимо додаткові змінні для зведення нерівностей до рівнянь:

Для зведення задачі до канонічної форми помножимо кожне рівняння на (–1):

Очевидно, що в даному разі штучні змінні необхідно вводити в перші два рівняння. У третьому рівнянні базисною змінною буде w ₁. Маємо таку задачу лінійного програмування:

,

.

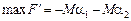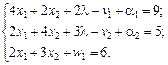
Розв’язавши її симплексним методом, отримаємо:

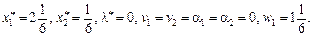
Необхідно перевірити виконання умов:

;

;

.

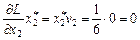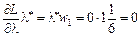Всі умови виконуються, отже, 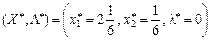є сідловою точкою функції Лагранжа для задачі квадратичного програмування, а — оптимальним планом задачі, для якого значення функціонала дорівнює:

.

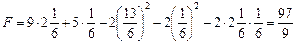8.9. Економічна інтерпретація множників Лагранжа

Теорему 8.4 можна розглядати як узагальнення другої теореми двоїстості задач лінійного програмування для задач нелінійного програмування. Умови (8.39)—(8.41) є умовами доповнюючої нежорсткості.

Для з’ясування питання стосовно економічного змісту множників Лагранжа розглянемо застосування методу множників Лагранжа до задачі лінійного програмування як частинного випадку нелінійних задач. Нехай задача має вигляд:

max F = c ₁ x ₁+ c ₂ x ₂+…+ c_nx_n (8.57)

(8.58)

Функція Лагранжа для даної задачі має вигляд:

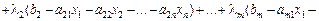
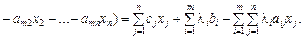
Якщо деякий змінний вектор 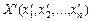є допустимим розв’язком задачі (8.57)—(8.58), то функція Лагранжа ідентич­на функції мети (8.57). Через те що виконуються умови 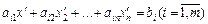, доданки виду 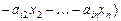у функції Лагранжа перетворюються в нуль і L (X',Λ)= F (X').

З необхідних умов існування екстремуму для функції Лагранжа можна помітити, що істотною для розгляду є лише умова рівності нулю частинних похідних L (X,Λ) по множниках Лагранжа. Отже, маємо задачу, що еквівалентна (8.57), (8.58):

max 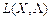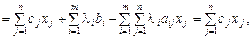(8.59)

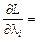
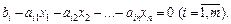(8.60)

Розглянемо другу групу умов існування екстремальних точок функції Лагранжа, коли частинні похідні по 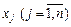дорівнюють нулю:

. (8.61)

Допустимо, що деякий вектор задовольняє умови (8.61), тоді для нього функція Лагранжа набуває вигляду:

.

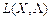
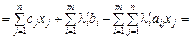
Причому для того, щоб задовольнити умову (8.59), необхідно знайти такі значення вектора, що , тобто приходимо до такої задачі:

, (8.62)

(8.63)

Очевидно (див. розділ 3), що пара задач (8.57), (8.58) та (8.62), (8.63) є парою спряжених задач (початковою та двоїстою), а множники Лагранжа — змінними двоїстої з цієї пари задач .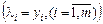

Отже, 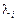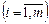— це двоїсті оцінки ресурсів, «тіньові» ціни відповідних ресурсів виробництва.

Якщо поширити ці висновки на загальну задачу нелінійного програмування, додавши до задачі (8.57), (8.58) умову , то розв’язування можна здійснювати узагальненням методу Лагранжа (§ 8.4).

В результаті отримаємо двоїсту задачу, що має вигляд:

,

,

.

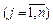Звідси отримуємо економічну інтерпретацію змінних парамет­рів початкової задачі, а також множників Лагранжа.

Очевидно, що залежно від економічної постановки задачі, функ­ція Лагранжа та умови існування сідлової точки можуть мати різ­ну економічну інтерпретацію. Розглянемо задачу нелінійного програмування стосовно визначення оптимального плану виробництва продукції за умов використання обмежених ресурсів:

max F = f (x ₁, x ₂,… x_n),

,

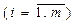Головна мета виробничої системи — максимізація прибутку від реалізованої продукції. Отже, цільова функція F=f (X) — це прибуток від реалізації продукції в обсягах , причому f (X) — нелінійна. Крім того, для виробництва продукції необхідне використання m видів сировини, обсяги кожного виду якої відомі і становлять b_i 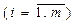. Система рівнянь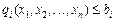 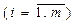може бути подана у вигляді: 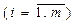. Тобто, q_i (X) — обсяг і -го виду сировини, що використовується для виробництва продук­ції в обсязі Х, тоді g_i (X) — лишок і -го ресурсу після виробницт­ва продукції. Якщо g_i (X)>0, то це означає, що на виробництво продукції використано не весь запас ресурсу, а якщо g_i (X)=0 — ресурс вичерпано і якщо g_i (X)<0, то це значить, що наявної (початкової) кількості сировини недостатньо для виробництва продукції на рівні Х.

Виробнича система здебільшого функціонує в конкурентному середовищі, що характеризується антагоністичними інтересами.

Як було показано вище, 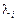— це змінні двоїстої до поставленої певної задачі. Вони можуть являти собою ціну, за якою на конкурентному ринку продається чи купується одиниця і -го виду сировини. Якщо 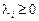і g_i (X)>0, то така виробнича система може продати лишки сировини і отримати додатковий прибуток у розмірі . Якщо g_i (X)<0, то підприємство може закупити потрібну кількість сировини, витративши суму грошей, що дорівнює . Така закупівля дасть змогу забезпечити виробництво продукції на рівні Х. Отже, функція Лагранжа

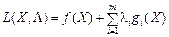
являє собою загальний прибуток від виробництва, який включає прибуток від реалізації виготовленої продукції f (X) та прибуток від продажу лишків сировини (чи витрати на придбання потрібної кількості сировини) .

За цін 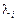, що встановлюються на ринку, виробнича система прагне максимізувати прибуток шляхом визначення оптимального обсягу виробництва продукції 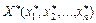. Отже, знаходиться значення функції Лагранжа при Х ^*:

.

Оскільки прибуток формується на конкурентному ринку, слід розраховувати на встановлення цін на ресурси на мінімально мож­ливому рівні, тобто слід відшукати

.

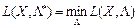Якщо для розглянутої задачі нелінійного програмування існує сідлова точка 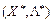, то це означає, що існує такий рівень вироб­ництва 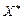та цін на ресурси 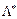, за яких має місце конкурентна рівновага:

=

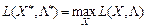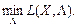
Оскільки за теоремою Куна — Таккера для сідлової точки за будь-яких значень виконується нерівність:

,

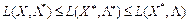то очевидно, що ніяка зміна рівня виробництва 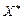виробничою системою не збільшить прибутку і також ніяка зміна цін на ресурси в ринковому середовищі не зможе змен­шити прибутку 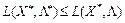. Отже, сідлова точка функції Лагранжа є точкою ринкової рівноваги.

Розглянемо інтерпретацію множників Лагранжа. Позначимо через 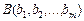вектор з компонентами, що означають обсяг і -го ресурсу у виробничій системі. Нехай означає, що оптимальний план задачі є функцією від значень наявних ресурсів В. Для спрощення допустимо, що функції та f (X), q_i (X) 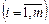мають властивості неперервності та диференційовності. І нарешті, допустимо також, що коли для і -го ресурсу , то за невеликих змін значення вектора В (що позначимо через ), які є досить близькими до В, також виконується нерівність g_i (X (B'))>0.

За теоремою Куна — Таккера в задачах нелінійного програмування з обмеженнями — нерівностями для оптимального плану задачі має місце рівність ([3]):

.

Використовуючи правило диференціювання складної функції, можна написати таку рівність:

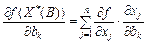. Враховуючи, що , маємо:

.

Тепер допустимо, що деяке і -те обмеження активне в точці В, тобто 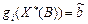. Тоді згідно з початковим допущенням це обмеження активне також і в деякому невеликому околі цієї точки. Враховуючи це, матимемо:

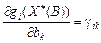, де

Отже,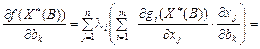

Тому 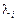є маргінальними змінами оптимального значення цільової функції за зміни . Аналогічно, як і в задачах лінійного програмування, можна вважати, що 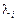приблизно відповідає приросту цільової функції за збільшення обсягу відповідного і -го ресурсу на одиницю. Виходячи з цього, можна оцінити, як зміниться оптимальне значення цільової функції за змін обсягів ресурсів, не розв’язуючи нову задачу.

8.10. Градієнтний метод

Градієнтні методи належать до наближених методів розв'язування задач нелінійного програмування і дають лише певне наближення до екстремуму, причому за збільшення обсягу обчислень можна досягти результату з наперед заданою точністю, але в цьому разі є можливість знаходити лише локальні екстремуми цільової функції. Зауважимо, що такі методи можуть бути застосовані лише до тих типів задач нелінійного програмування, де цільова функція і обмеження є диференційовними хоча б один раз. Зрозуміло, що градієнтні методи дають змогу знаходити точки глобального екстремуму тільки для задач опуклого програмування, де локальний і глобальний екстремуми збігаються.

В основі градієнтних методів лежить основна властивість градієнта диференційовної функції — визначати напрям найшвидшого зростання цієї функції. Ідея методу полягає у переході від однієї точки до іншої в напрямку градієнта з деяким наперед заданим кроком.

Розглянемо метод Франка — Вульфа, процедура якого передбачає визначення оптимального плану задачі шляхом перебору розв’язків, які є допустимими планами задачі.

Нехай необхідно відшукати

max F = f (x ₁, x ₂,… x_n)

за лінійних обмежень:

;

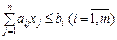Допустимо, що Х ₀ — початкова точка, що належить множині допустимих планів даної задачі. В деякому околі цієї точки нелінійну цільову функцію замінюють лінійною і потім розв’язують задачу лінійного програмування. Нехай розв’язок лінійної задачі дав значення цільової функції F ₀, тоді з точки Х ₀ в напрямку F ₀ необхідно рухатись доти, поки не припиниться зростання цільової функції. Тобто у зазначеному напрямку вибирають наступну точку Х ₁, цільова функція знову замінюється на лінійну, і знову розв’язується задача лінійного програмування.

Розглянемо детальніше перехід від k -ої ітерації методу до (k + 1)-ої ітерації.

Припустимо, що відома точка X_k, яка належить області допустимих розв’язків. У даній точці обчислюємо градієнт цільової функції:

.

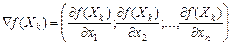Значення градієнта функції задає в даній точці напрям най­швидшого її зростання.

Замінюємо цільову функцію задачі лінійною функцією виду:

.

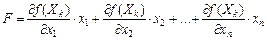Потім розв’язуємо задачу лінійного програмування з обмеженнями початкової задачі і новою цільовою функцією:

за умов:

;

.

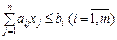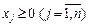Нехай розв’язком такої задачі є точка .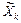

З початкової точки в напрямку 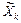рухаємося з деяким довільним кроком 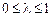, визначаючи координати нової точки Х_{k +1} у такий спосіб:

Зауважимо, що значення параметра 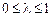доцільно вибирати таким, що дає найбільше значення цільової функції початкової задачі .

Для точки Х_{k +1} повторюємо розглянутий процес, для чого знову розраховуємо значення градієнта і т. д.

У такий спосіб знаходимо послідовність точок X ₀, X ₁,…, які поступово наближаються до оптимального плану початкової задачі. Ітераційний процес повторюється до того моменту, поки значення градієнта цільової функції не стане рівним нулю або виконуватиметься умова |f(X_{k +1})-f(X_k)|<ε, де ε — досить мале число, яке означає потрібну точність обчислень.

Підприємство виробляє два види продукції (А і В) і використовує на виробництво три види ресурсів: І, ІІ, ІІІ. Витрати ресурсів на виробництво одиниці кожного виду продукції подано в табл. 8.2.

Таблиця 8.2

Вид ресурсу	Вид продукції	Загальний обсяг ресурсу
А	В
І
ІІ
ІІІ

Ціна реалізації одиниці продукції виду А становить 20 ум. од., проте прибуток залежить від витрат на виробництво, які пропорційні квадрату кількості виготовленої продукції. Аналогічно визначається прибуток для продукції виду В, ціна реалізації якої дорівнює 18 ум. од.

Розв’язання. Позначимо через х ₁ кількість продукції виду А, х ₂ — кількість продукції виду В, тоді загальний прибуток матиме вигляд: .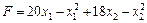

Математична модель задачі має вигляд:

max F =20 x ₁ – x ₁²+18 x ₂ – x ₂²),

.

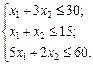
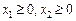Розв’яжемо задачу методом Франка Вульфа.

Дата добавления: 2014-11-29