Краткие теоретические сведения. Порядок выполнения лабораторной работы

Лабораторная работа № 4

Порядок выполнения лабораторной работы

1. По виду построенной в лабораторной работе № 1 гистограммы сделать предположение о законе распределения.

2. Найти параметры предполагаемого распределения методом моментов и максимального правдоподобия.

3. Уточнить параметры распределения методом наименьших квадратов. Оценить норму среднеквадратичного отклонения по серединам интервалов.

4. Выполнить сравнительный анализ полученных результатов.

5. Все найденные аналитические зависимости изобразить графически.

Тема: «Проверка статистических гипотез. Параметрические гипотезы»

Цель работы: получение практических навыков в формировании и проверке статистических гипотез параметрического типа. Построение допустимой и критических областей с заданным уровнем доверительной вероятности и получение оценок.

Статистической гипотезой называют предположение о параметрах или виде распределения случайной величины. Статистическая гипотеза называется простой, если она содержит только одно предположение. Например: если – параметр показательного распределения, то гипотеза 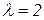– простая. Простой будет являться и гипотеза о том, что случайная величина распределена по нормальному закону с параметрами .

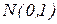Сложной называют гипотезу, состоящую из конечного или бесконечного числа простых гипотез. Сложная гипотеза для параметра показательного распределения состоит из бесчисленного множества простых вида 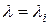, где – любое число, большее 2. Сложной будет и гипотеза о том, что случайная величина распределена по нормальному закону с параметрами , где .

Гипотезы называются параметрическими, если распределение случайной величины Х известно, и по выборке наблюдений необходимо проверить предположения о значении параметров этого распределения.

Проверяемая гипотеза называется нулевой (основной) и обозначается 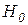. Наряду с выдвинутой основной гипотезой рассматривают и одну из противоречащих ей (конкурирующих, альтернативных), которую обозначают . Если выдвинутая гипотеза 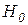будет отвергнута, то имеет место противоречащая гипотеза. Следовательно, эти гипотезы целесообразно различать. Например, если проверяется основная гипотеза о равенстве параметра показательного распределения, т.е. 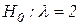, то в качестве конкурирующей может быть выбрана одна из следующих гипотез

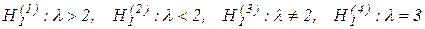и т.д.

Выбор альтернативной гипотезы определяется конкретной формулировкой задачи. Выдвинутая основная гипотеза может быть правильной или неправильной, поэтому возникает необходимость ее проверки. Поскольку проверку производят статистическими методами, ее называют статистической. В итоге статистической проверки гипотезы в двух случаях может быть принято неправильное решение, т. е. могут быть допущены ошибки двух видов. Ошибка первого рода состоит в том, что будет отвергнута правильная гипотеза. Ошибка второго рода состоит в том, что будет принята неправильная гипотеза. Вероятность совершить ошибку первого рода принято обозначать через , ее называют уровнем значимости. Наиболее часто уровень значимости принимают равным 0.05, 0.01 или 0.001. Если, например, принят уровень значимости, равный 0.05, то это означает вероятность допустить ошибку первого рода (отвергнуть правильную гипотезу).

Статистический критерий проверки нулевой гипотезы

Для проверки нулевой гипотезы используют специально подобранную случайную величину, точное или приближенное распределение которой известно. Эту величину обозначают через U, если она распределена нормально, F, если имеет место распределение Фишера, T – распределение Стьюдента, – закон «хи-квадрат» и т. д. Все эти случайные величины обозначим через Z. Тогда правило, по которому принимается решение принять или отклонить гипотезу 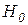, назовем критерием К. Так как решение принимается на основе выборки наблюдений случайной величины Х, необходимо подобрать подходящую статистику, называемую в этом случае статистикой Z критерия К. Наблюдаемым значением назначают значение критерия, вычисленное по выборкам.

Статистическим критерием (или просто критерием) называют случайную величину Z, которая служит для проверки нулевой гипотезы.

Для проверки гипотезы по данным выборок вычисляют частные значения входящих в критерий величин, и таким образом получают частное (наблюдаемое) значение критерия. После выбора определенного критерия множество всех его возможных значений разбивают на два непересекающихся подмножества: одно из них содержит значения критерия, при которых нулевая гипотеза отвергается, а другое – при которых она принимается.

Критической областью называют совокупность значений критерия, при которых нулевую гипотезу отвергают. Областью принятия гипотезы (областью допустимых значений) называют совокупность значений критерия, при которых гипотезу принимают.

Основной принцип проверки статистических гипотез можно сформулировать так: если наблюдаемое значение критерия принадлежит критической области – гипотезу отвергают, если наблюдаемое значение критерия принадлежит области принятия гипотезы – гипотезу принимают.

Поскольку критерий К – одномерная случайная величина, все ее возможные значения принадлежат некоторому интервалу. Поэтому критическая область и область принятия гипотезы также являются интервалами и, следовательно, существуют точки, которые их разделяют.

Критическими точками (границами) называют точки, отделяющие критическую область от области принятия гипотезы.

Различают одностороннюю (правостороннюю или левостороннюю) или двустороннюю критические области.

Правосторонней называют критическую область, определяемую неравенством , где – положительное число.

Левосторонней называют критическую область, определяемую неравенством 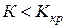, где – отрицательное число.

Односторонней называют правостороннюю или левостороннюю критическую область.

Двусторонней называют критическую область, определяемую неравенствами 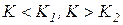, где . В частности, если критические точки симметричны относительно нуля, двусторонняя критическая область определяется неравенством .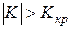

Правосторонняя критическая область. Критическая область для правостороннего критерия определяется неравенством , где 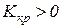. Для отыскания правосторонней критической области необходимо найти критическую точку. С этой целью задаются достаточно малой вероятностью – уровнем значимости. Затем ищут критическую точку 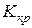, исходя из требования 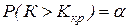, чтобы при условии справедливости нулевой гипотезы вероятность того, что критерий К примет значение , была равна принятому значению уровня значимости. Для каждого критерия имеются соответствующие таблицы, по которым находят критическую точку, удовлетворяющую этому требованию. Когда критическая точка уже найдена, вычисляют по выборкам наблюденное значение критерия и, если окажется, что , то нулевую гипотезу отвергают; если же 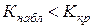, то нет оснований, чтобы отвергнуть нулевую гипотезу.

Поскольку вероятность события мала ( – малая вероятность), такое событие при справедливости нулевой гипотезы в силу принципа практической невозможности маловероятных событий в единичном испытании не должно наступить. Если все же оно произошло, т. е. наблюдаемое значение критерия оказалось больше , то это можно объяснить тем, что нулевая гипотеза ложна и, следовательно, должна быть отвергнута. Таким образом, требование 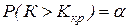определяет такие значения критерия, при которых нулевая гипотеза отвергается, а они составляют правостороннюю критическую область.

Наблюдаемое значение критерия может оказаться большим 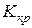не потому, что нулевая гипотеза ложна, а по другим причинам (малый объем выборки, недостатки методики эксперимента и др.). В этом случае, отвергнув правильную нулевую гипотезу, совершают ошибку первого рода. Вероятность этой ошибки равна уровню значимости .

Левосторонняя критическая область

Отыскание левосторонней и двусторонней критических областей сводится (так же как и для правосторонней) к нахождению соответствующих критических точек. Левосторонняя критическая область определяется неравенством .

Критическую точку находят, исходя из требования, чтобы при справедливости нулевой гипотезы вероятность того, что критерий имеет значение, меньшее 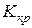, была равна принятому уровню значимости: .

Двусторонняя критическая область определяется неравенствами: . Критические точки находят, исходя из требования, чтобы при справедливости нулевой гипотезы сумма вероятностей того, что критерий примет значение, меньшее и большее 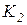, была равна принятому уровню значимости: 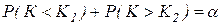. Ясно, что критические точки могут быть выбраны множеством способов. Если распределение критерия симметрично относительно нуля, то, зная, что 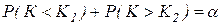, получим . Это соотношение и служит для отыскания критических точек двусторонней критической области. Критические точки находят по соответствующим таблицам.

Пример 1. Изнормальной генеральной совокупности извлечена выборка объема n=24 и по ней найдена исправленная выборочная дисперсия s²=17,2, генеральная дисперсия 15,1. При уровне значимости α=0,05 проверить гипотезу H0: δ² = δ₀² , если альтернативная гипотеза H1: δ² > δ₀²

Критическая область правосторонняя.

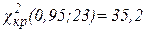
, т.к. 26,2<35,2 то принимаем основную гипотезу H0.

Пример 2. По двум независимым выборкам n1=13 и n2=15 извлеченным из нормальных генеральных совокупностей X1 и X2 с дисперсиями δ₁²=9, δ₂²=12. Оценки математических ожиданий . При уровне значимости α=0,05 проверить гипотезу H0: , если альтернативная гипотеза
H1: .

Критическая область двусторонняя.

Критерий: , основная гипотеза принимается.

Контрольные вопросы

1. Дать определение статистической гипотезы.

2. Определить понятие простой и сложной, параметрической и непараметрической гипотез. Привести примеры.

3. Нулевая и альтернативная гипотезы. Статистика критерия. Статистический критерий.

4. Критическая область и область принятия основной гипотезы. Уровень значимости.

5. Двусторонний, односторонний: правосторонний и левосторонний критерии. Неравенства для критической области.

6. Схема проверки простой параметрической гипотезы.

7. Статистические ошибки первого и второго рода

Дата добавления: 2014-11-29