Зразки розв’язування задач

Приклад 1. (Задача 1.1) Розв'язати систему лінійних рівнянь

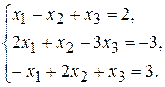
двома способами:

а) за правилом Крамера;

б) матричним способом.

Розв'язання.

а) Обчислимо визначник матриці системи

.

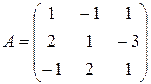Маємо

Так як визначник системи 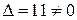, то система має єдиний розв'язок, який можна знайти за формулами Крамера:

.

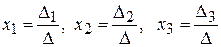В цьому прикладі маємо

Підставивши знайдені значення визначників у формули Крамера, отримаємо

.

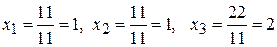б) Знайдемо розв'язок системи матричним способом.

Дана система рівносильна наступному матричному рівнянню

,

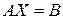де

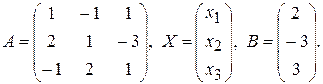
Якщо 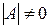, то розв'язок системи можна знайти за формулою

,

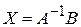де 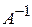– обернена до А матриця, що має вигляд

.

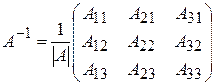Так як 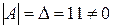, то матриця А має обернену.

Знаходимо матрицю 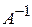, обернену до А. Обчислимо алгебраїчні доповнення елементів матриці А:

.

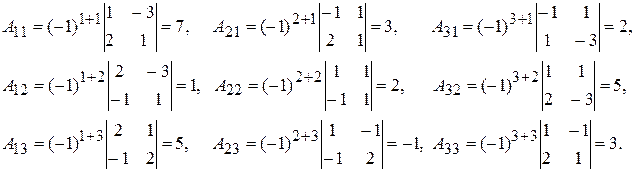
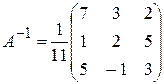Розв'язок системи запишемо за формулою (6) у вигляді:

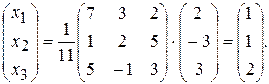
Звідси .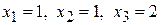

Приклад 2. (Задача 1.2)

а) Підприємство випускає чотири види виробів П ₁, П ₂, П ₃, П ₄ з використанням чотирьох типів сировини S ₁, S ₂, S ₃, S ₄. Норми витрат сировини задано матрицею

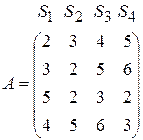
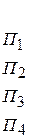
Треба знайти витрати сировини кожного типу при заданому плані випуску кожного виду виробів

.

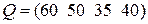Розв'язання.

Очевидно, що витрати П сировини кожного типу можна обчислити, користуючись формулою

.

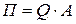Тоді

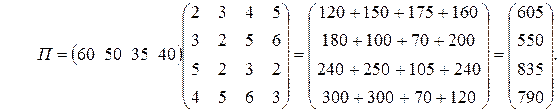
Отже, витрати сировини кожного типу становлять відповідно 605, 550, 835 та 790 одиниць.

б) Взуттєва фабрика спеціалізується з випуску трьох типів продукції П ₁, П ₂, П ₃, використовуючи при цьому сировину трьох видів S ₁, S ₂, S ₃. Норми витрат кожної сировини на одну пару взуття і обсяг витрат сировини на один день задані таблицею 3.

Таблиця 3.

Вид сировини	Витрати сировини на одиницю продукції	Запаси сировини
П 1	П 2	П 3
S 1
S 2
S 3

Знайти щоденний обсяг випуску кожного типу взуття.

Розв'язання.

Нехай щоденно фабрика випускає 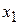пар виробів П ₁, 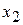пар виробів П ₂ і пар виробів П ₃. Тоді згідно з витратами сировини кожного виду маємо систему рівнянь

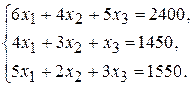
Розв'яжемо дану систему за формулами Крамера:

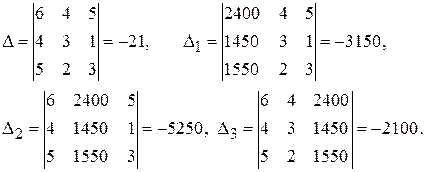
Отже,

,

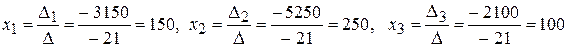а це означає, що фабрика випускає 150 пар взуття типу П ₁, 250 пар взуття типу П ₂ і 100 пар взуття типу П ₃.

Приклад 3. (Задача 1.3)

Розв'язати систему лінійних рівнянь методом Гаусса.

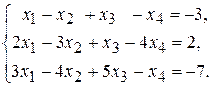
Розв'язання.

Маємо

Отже, 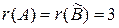. Система сумісна. Оскільки ранг менший числа невідомих, то система має безліч розв'язків.

Перетворена система матиме вигляд

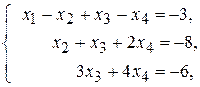або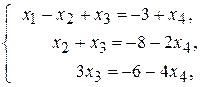

де 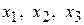– базисні, а 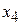– вільна невідома. Розв'язавши останню систему відносно 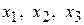, піднімаючись знизу вгору, знайдемо

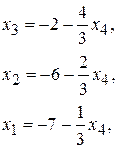
де 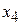набуває довільних значень.

Отже, 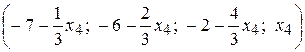, – розв’язок системи.

Дата добавления: 2014-11-29