
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Если же , то в силу (2.1) . 3 страница
|
|
|
|
Доказательство. Разложим определитель  по первой строке, получим
по первой строке, получим  =
=  +
+ 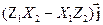 +
+ 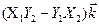 =
=  .
.
П р и м е р 26. Известно, что 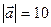 ,
, 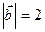 и
и 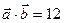 . Найти длину векторного произведения векторов
. Найти длину векторного произведения векторов  и
и  .
.
Решение. По определению векторного произведения  , где
, где  - угол между векторами. По формуле (2.22) имеем:
- угол между векторами. По формуле (2.22) имеем:  . Учитывая, что угол между векторами не превышает
. Учитывая, что угол между векторами не превышает 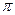 , из основного тригонометрического тождества получим:
, из основного тригонометрического тождества получим:  . Таким образом,
. Таким образом,  .
.
П р и м е р 27. Даны точки  ,
,  и
и 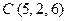 . Вычислить площадь
. Вычислить площадь  треугольника
треугольника  .
.
Решение. Площадь  треугольника
треугольника  равна половине площади
равна половине площади  параллелограмма, построенного на векторах
параллелограмма, построенного на векторах 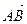 и
и  , т. е.
, т. е.  . Согласно (2.4)
. Согласно (2.4)  ,
,  , поэтому по формуле (2.29) имеем:
, поэтому по формуле (2.29) имеем: 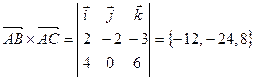 . Тогда
. Тогда  .
.
П р и м е р 28. Найти вектор  , зная, что он перпендикулярен векторам
, зная, что он перпендикулярен векторам  и
и 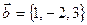 и удовлетворяет условию
и удовлетворяет условию  .
.
Решение. Пусть вектор  имеет координаты
имеет координаты  . Тогда условие
. Тогда условие  можно записать в виде
можно записать в виде  . Вектор
. Вектор  перпендикулярен векторам
перпендикулярен векторам  и
и  , поэтому он коллинеарен вектору
, поэтому он коллинеарен вектору  . По формуле (2.29)
. По формуле (2.29)  . Условие коллинеарности векторов
. Условие коллинеарности векторов  и
и  согласно (2.28) имеет вид
согласно (2.28) имеет вид  . Поэтому для неизвестных
. Поэтому для неизвестных  получили систему уравнений
получили систему уравнений 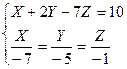 , решив которую найдем, что
, решив которую найдем, что 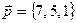 .
.
2.8. Смешанное произведение трех векторов
Пусть даны три произвольных вектора  ,
,  и
и  .
.
Определение. Смешанным произведением трех векторов  ,
,  ,
,  называется скалярное произведение вектора
называется скалярное произведение вектора  на векторное произведение векторов
на векторное произведение векторов  и
и  , т. е.
, т. е.
 . (2.30)
. (2.30)
Геометрический смысл смешанного произведения раскрывает следующая теорема.
Теорема 13. Смешанное произведение  равно объему параллелепипеда, построенного на приведенных к общему началу векторах
равно объему параллелепипеда, построенного на приведенных к общему началу векторах  ,
,  и
и  , взятому со знаком плюс, если тройка векторов
, взятому со знаком плюс, если тройка векторов  правая, и со знаком минус, если тройка
правая, и со знаком минус, если тройка  левая. Если же векторы
левая. Если же векторы  ,
,  и
и  компланарны, то
компланарны, то 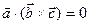 .
.
Доказательство. Если векторы  и
и  коллинеарны, то векторы
коллинеарны, то векторы  ,
,  и
и  компланарны. Для компланарных векторов
компланарны. Для компланарных векторов  и
и  по свойству векторного произведения
по свойству векторного произведения  , поэтому по свойству скалярного произведения
, поэтому по свойству скалярного произведения  , т. е. для компланарных векторов теорема доказана.
, т. е. для компланарных векторов теорема доказана.
|
|
|
Пусть векторы  ,
,  и
и  не компланарны. Приведем эти векторы к общему началу
не компланарны. Приведем эти векторы к общему началу 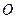 . По формуле (2.23)
. По формуле (2.23)  , где
, где  - площадь параллелограмма, построенного на приведенных к общему началу векторах
- площадь параллелограмма, построенного на приведенных к общему началу векторах  и
и  ,
,  - орт векторного произведения
- орт векторного произведения 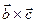 . Тогда
. Тогда
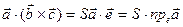 . (2.31)
. (2.31)
Проекция вектора  на ось, определяемую вектором
на ось, определяемую вектором  , с точностью до знака равна высоте
, с точностью до знака равна высоте 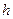 параллелограмма, построенного на приведенных к общему началу векторах
параллелограмма, построенного на приведенных к общему началу векторах  ,
,  и
и  , при условии, что основанием служит параллелограмм, построенный на векторах
, при условии, что основанием служит параллелограмм, построенный на векторах  и
и  .
.
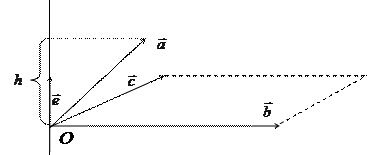 |
Таким образом, правая часть равенства (2.31) с точностью до знака равна объему параллелепипеда, построенного на векторах  ,
,  и
и  . Если векторы
. Если векторы  и
и  лежат по одну сторону от плоскости, определяемой векторами
лежат по одну сторону от плоскости, определяемой векторами  и
и  , то
, то 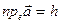 , если же векторы
, если же векторы  и
и  лежат по разные стороны от этой плоскости, то
лежат по разные стороны от этой плоскости, то 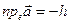 . Векторы
. Векторы  ,
,  и
и  образуют правую тройку по определению векторного произведения
образуют правую тройку по определению векторного произведения 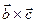 , таким образом,
, таким образом, 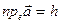 , если векторы
, если векторы  ,
,  и
и  (соответственно векторы
(соответственно векторы  ,
,  и
и  ) образуют правую тройку, и
) образуют правую тройку, и 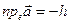 , если тройка векторов
, если тройка векторов  левая.
левая.
Если векторы  ,
,  и
и  компланарны, то вектор
компланарны, то вектор  лежит в плоскости векторов
лежит в плоскости векторов  и
и  , следовательно,
, следовательно, 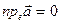 , и
, и 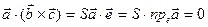 . Теорема доказана.
. Теорема доказана.
Из этой теоремы следует, что объем параллелепипеда, построенного на приведенных к общему началу векторах  ,
,  и
и  , вычисляется по формуле
, вычисляется по формуле
 . (2.32)
. (2.32)
Следствие 1. Для любых трех векторов  ,
,  и
и  справедливо равенство
справедливо равенство
 . (2.33)
. (2.33)
Доказательство. Из переместительного свойства скалярного произведения следует  , поэтому достаточно доказать, что
, поэтому достаточно доказать, что  . Последнее равенство выполняется с точностью до знака, потому что обе его части с точностью до знака определяют объем параллелепипеда, построенного на векторах
. Последнее равенство выполняется с точностью до знака, потому что обе его части с точностью до знака определяют объем параллелепипеда, построенного на векторах  . Но тройки векторов
. Но тройки векторов  и
и  одновременно являются либо правыми, либо левыми, следовательно, знаки выражений
одновременно являются либо правыми, либо левыми, следовательно, знаки выражений 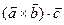 и
и 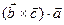 совпадают. Таким образом,
совпадают. Таким образом,  . Следствие доказано.
. Следствие доказано.
|
|
|
Доказанное равенство (2.33) позволяет записывать смешанное произведение трех векторов  ,
,  и
и  просто в виде
просто в виде 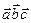 , без указания при этом, какие два вектора (первые два или последние два) перемножаются векторно.
, без указания при этом, какие два вектора (первые два или последние два) перемножаются векторно.
Следствие 2. Три вектора компланарны тогда и только тогда, когда их смешанное произведение равно нулю.
Доказательство. Если векторы компланарны, то, согласно доказанной теореме, их смешанное произведение равно нулю. Если смешанное произведение векторов равно нулю, то по этой же теореме проекция одного из векторов на ось, определяемую векторным произведением двух других векторов, равна нулю, т. е. он параллелен плоскости, в которой лежат два другие вектора. Это означает, что векторы компланарны. Следствие доказано.
Следствие 3. Смешанное произведение трех векторов, два из которых совпадают, равно нулю.
Доказательство. Если два вектора из трех совпадают, то такие три вектора компланарны и их смешанное произведение равно нулю. Следствие доказано.
Теорема 14. Если векторы  ,
,  и
и  заданы своими координатами, т. е.
заданы своими координатами, т. е. 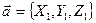 ,
,  ,
, 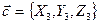 , то смешанное произведение векторов
, то смешанное произведение векторов  ,
,  и
и  вычисляется по формуле
вычисляется по формуле
 . (2.34)
. (2.34)
Доказательство. Разложим определитель, стоящий в правой части выражения (2.34), по первой строке. Получим: 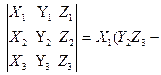
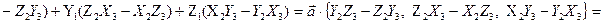
 . Теорема доказана.
. Теорема доказана.
Теорема 15.Пусть даны точки  ,
, 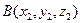 ,
,  ,
,  . Тогда объем параллелепипеда, построенного на векторах
. Тогда объем параллелепипеда, построенного на векторах 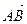 ,
,  и
и  как на сторонах, вычисляется по формуле
как на сторонах, вычисляется по формуле
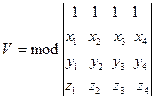 . (2.35)
. (2.35)
Доказательство. Преобразуем правую часть (2.35), используя свойства определителей:
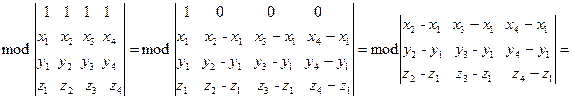
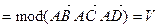 . Теорема доказана.
. Теорема доказана.
Следствие. Объем треугольной пирамиды с вершинами в точках  ,
, 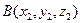 ,
,  ,
,  вычисляется по формуле
вычисляется по формуле
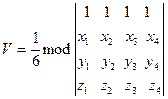 . (2.36)
. (2.36)
Доказательство. Если четыре вершины параллелепипеда, не лежащие в одной плоскости, являются вершинами треугольной пирамиды, то объем пирамиды составляет 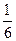 объема параллелепипеда. Учитывая, что объем параллелепипеда вычисляется по формуле (2.35), получаем доказываемое тождество. Следствие доказано.
объема параллелепипеда. Учитывая, что объем параллелепипеда вычисляется по формуле (2.35), получаем доказываемое тождество. Следствие доказано.
П р и м е р 29. Вершины тетраэдра находятся в точках  ,
, 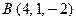 ,
,  и
и 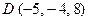 . Найти длину высоты
. Найти длину высоты 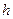 тетраэдра, опущенной из вершины
тетраэдра, опущенной из вершины  .
.
Решение. Так как объем  тетраэдра и его высота
тетраэдра и его высота 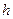 связаны соотношением
связаны соотношением 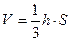 , где
, где  - площадь грани
- площадь грани  , то
, то 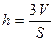 . Объем
. Объем  тетраэдра и площадь
тетраэдра и площадь  грани
грани  найдем, используя векторное и смешанное произведения векторов. По формуле (2.36) имеем:
найдем, используя векторное и смешанное произведения векторов. По формуле (2.36) имеем:  . Из определения векторного произведения следует, что
. Из определения векторного произведения следует, что  . Так как
. Так как  ,
,  , то
, то 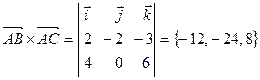 и
и 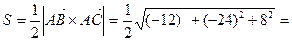
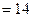 . Таким образом,
. Таким образом, 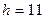 .
.
|
|
|
|
|
|
|
|
Дата добавления: 2014-11-29; Просмотров: 211; Нарушение авторских прав?; Мы поможем в написании вашей работы!