Способи опису руху точки

Векторний спосіб. Цей спосіб знайшов широке застосування у теоретичних розрахунках. Розглянемо сутність цього способу.

Припустимо, що довільна точка М рухається у просторі по деякій траєкторії (рис.2.1). візьмемо у просторі прямокутну декартову систему координат xOyz з одиничними векторами (ортами) . З початку системи координат точки О проведемо до точки М радіус-вектор 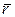. При русі точки М її радіус-вектор 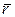буде з плином часу змінюватися за величиною (модулем) та напрямом. Таким чином, якщо буде заданий закон зміни радіус-вектора 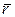рухомої точки М як функція часу, то рух матеріальної точки вважається заданим векторним способом. Математично це можна записати так:

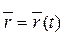, (2.1)

де t - час.

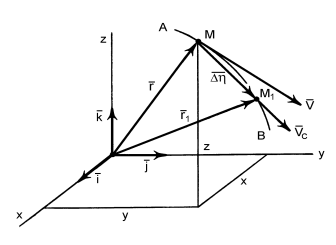
Рис.2.1

Співвідношення (2.1) називається кінематичним рівнянням руху точки у векторній формі. Одночасно цей вираз можна розглядати як рівняння траєкторії.

Знайдемо у прийнятій системі координат Oxyz величину радіус-вектора 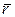, для чого спроектуємо його на осі координат. Отримаємо:

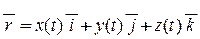, (2.2)

де , , 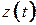- поточні значення координат кінця радіус-вектора 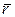або, фактично, рухомої точки М.

Визначимо кінематичні характеристики рухомої точки М.

Траєкторією АВ руху матеріальної точки М є геометричне місце кінців радіус-вектора 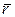або неперервна лінія, яку описує точка під час свого руху відносно даної системи відліку.

Введемо поняття годографа векторної функції 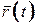(2.1) по скалярному аргументу t. Це крива, яка накреслюється кінцем вектора 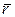при неперервній зміні часу t, коли початок вектора залишається у фіксованій точці О. Тобто, годограф описують кінці векторів , що відповідають конкретним положенням точки у процесі руху. Це стосується не тільки радіус-векторів, а і векторів швидкості, прискорень тощо. В даному разі годограф співпадає з траєкторією АВ.

Визначимо другу кінематичну характеристику – швидкість руху матеріальної точки М.

Швидкість – це векторна величина, яка характеризує зміну переміщення за одиницю часу , .

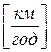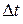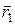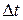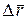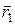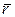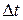Для цього розглянемо рух точки М. Вважаємо, що точка рухається по довільній траєкторії АВ (рис.2.1). за деякий проміжок часу точка перемістилась із положення М в положення (радіус-вектор ). Для того, щоб визначити переміщення точки М за проміжок часу ,з'єднаємо точки М і М ₁ і отримаємо вектор , який є геометричною різницею між векторами і . Тоді середня швидкість точки за проміжок часу (згідно визначення) дорівнює відношенню 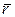до 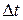, а саме:

,

а швидкість точки у будь-який момент часу буде дорівнювати:

. (2.4)

Як бачимо з останнього виразу, при векторному способі задання руху матеріальної точки її швидкість є першою похідною від радіус-вектора точки по часу.

Напрямок вектора швидкості 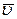точки – по дотичній до траєкторії і спрямований у бік її руху.

Прискорення – це векторна величина, яка характеризує зміну вектора швидкості за одиницю часу.

Одиниця виміру прискорення – .

Визначимо прискорення матеріальної точки М. Розглянемо рух точки у площині і вважаємо, що вона рухається по довільній траєкторії (рис.2.2). У положенні М швидкість точки була 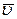. За деякий проміжок часу 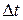точка перемістилась у положення М ₁, а її швидкість змінилась і стала дорівнювати . Вказані вектори швидкостей точки будуть спрямовані по дотичних до траєкторії. Знайдемо приріст швидкості за даний проміжок часу. Для цього перенесемо паралельно вектор швидкості у положення М. З'єднаємо кінці векторів 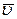і і отримаємо вектор . 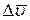Відношення приросту 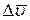вектора 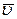до проміжку часу 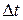згідно визначення прискорення і буде середнім прискоренням рухомої матеріальної точки М. А саме:

(2.5)

Вектор буде паралельним вектору 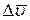, але не має точки прикладання.

Рис.2.2

Для отримання миттєвого прискорення матеріальної точки необхідно розглянути нескінченно малий проміжок часу (тобто 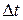→ 0), а весь вираз (2.5) звести до границі. Отримаємо:

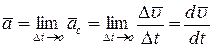. (2.6)

Якщо підставити у (2.6) значення швидкості точки (2.4), то матимемо:

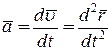. (2.7)

Таким чином, при векторному способі задавання руху матеріальної точки її прискорення дорівнює першій похідній від швидкості руху точки по часу, або другій похідній від радіус-вектора точки по часу.

Вектор миттєвого прискорення матеріальної точки буде спрямований у бік угнутості траєкторії, тобто її центра кривизни. Більш детально про напрямок вектора прискорення матеріальної точки буде розглянуто далі.

Координатний спосіб. Цей спосіб опису руху матеріальної точки широко використовується при розв'язанні задач, у технічних розрахунках.

При такому способі задавання руху матеріальної точки наперед задаються координати матеріальної точки як функції часу. Якщо вибрати у просторі прямокутну декартову систему координат Oxyz, то при русі точки М всі три її координати будуть змінюватися з часом (рис.2.1). Для того, щоб знати положення точки у будь-який момент часу, а також для визначення її кінематичних характеристик, необхідно задати вирази цих координат як функції часу. В загальному вигляді це можна записати так:

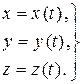(2.8)

Ці параметричні рівняння, в яких роль параметра відіграє час t, є кінематичними рівняннями руху точки у прямокутній декартовій системі координат і визначають суть даного способу.

Слід зауважити, що якщо рух матеріальної точки здійснюється в одній площині, то в системі (2.8) закон зміни однієї з координат вже не потрібний. Якщо рух точки здійснюється, наприклад, у площині xOy, то система (2.8) набуває такого вигляду:

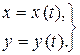(2.9)

Якщо матеріальна точка здійснює прямолінійний рух, то досить вибрати лише одну вісь координат, наприклад Ох, сумістивши її з напрямом руху, тоді цей рух буде описаний лише одним рівнянням:

. (2.10)

3. Основні кінематичні характеристики руху точки.

Визначимо кінематичні характеристики руху матеріальної точки при координатному способі опису її руху.

Траєкторія руху.

Рівняння (2.8) та (2.9) фактично є рівняннями траєкторії руху матеріальної точки у параметричній формі, в яких, як було сказано вище, роль параметра відіграє час . Для знаходження траєкторії руху у звичайній формі необхідно виключити з рівнянь руху час t, тобто здобути залежність між самими координатами. Це можна зробити декількома способами. Наприклад, підстановкою або піднесенням обох частин рівнянь до квадрату та по членним додаванням (якщо рівняння містять тригонометричні функції).

Дата добавления: 2014-11-29