Основы теории

ОСТАТОЧНЕ ОЗДОБЛЕННЯ

ВОЛОГО-ТЕПЛОВА ОБРОБКА СПІДНИЦІ

Заключна волого-теплова обробка включає в себе остаточне прасування виробу для надання йому гарного зовнішнього вигляду. При цьому розпрасовуються всі заломи тканини, прибирається полиск та відбитки на лицьовий бік припусків на шви, якщо це не було виконано у процесі пошиття при внутрішньо операційній волого-тепловій обробці.

Волого-теплова обробка виконується через пропрасувач – нефарбовану бавовняну тканину невеликого розміру.

Температура праски та час прасування повинні відповідати матеріалу виробу, що обробляється. Дію праски спочатку перевіряють на невеликому відрізку припуску на шов.

Шви припрасовують до повного прилягання, проте пам’ятайте, що збільшення тиску призводить до появи полиску, а подовження часу дії – до руйнування матеріалу.

Заключну волого-теплову обробку прямої двошовної спідниці виконують на столі зі спеціальним покриттям або на прасувальній дошці з виворотного боку виробу.

У спідниці в першу чергу відпрасувати виточки, складочки, шви.

Розмістити спідницю поясом до себе і відпрасувати пояс з внутрішнього боку не натискаючи на праску.

Повернути спідницю низом до себе і відпрасувати його з боку підгину слідкуючи за тим, щоб припуск на шов не відбивався на лицьовий бік.

Оздоблення використовують для прикрашання одягу. Це оздоблення декоративним шнуром, тасьмою, бісером, аплікацією, машинною строчкою та інше. Вид оздоблення, колір, форму обирають у відповідності до призначення одягу, волокнистою будовою, кольором тканини, фасоном виробу.

Остаточне оздоблення містить такі операції:

- обробка петель і пришивання фурнітури: ґудзиків, гачків і петель, кнопок тощо;

- прасування;

- чистка: в готовому виробі видаляються залишки ниток, крейди, чистять виріб з лицьового та виворотного боку.

При застібці пояса на гачки і петлі, гачки пришивають на відстані 0,5 см від бокових сторін і від кінця пояса з боку передньої частини спідниці. Застібнувши спідницю на тасьму-блискавку намічають місце розташування петель другому кінці пояса. Гачки і петлі пришивають 12 – 14 стібками.

При застібці пояса на петлю і ґудзик, петлю обробляють по середині пояса на баці передньої частини спідниці. При застібнутій тасьмі-блискавці намічають місце розташування ґудзика олівцем або крейдою і пришивають його на невеликій ніжці 3 – 4 стібками в кожну пару отворів.

1.1. Понятие о напряженном состоянии

Величина и направление вектора напряжения в точке зависят от того, как ориентирована проведенная плоскость сечения.

Возьмем упругое тело, на которое действуют нагрузки, и через точку А проведем ряд плоскостей сечения, тогда в каждом сечении в точке А будут действовать напряжения σ₁, σ₂,…, σ_n (рис. 1).

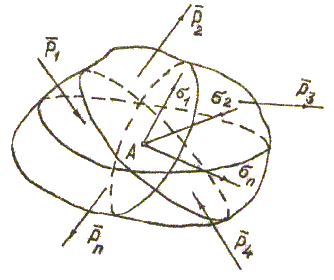
рис. 1

Через точку А можно провести бесчисленное множество плоскостей сечений, и в каждом из них будет действовать напряжение. Совокупность напряжений, действующих в данной точке во всех сечениях, проведенных через нее, называется напряженным состоянием в этой точке.

Для удобства изучения напряженного состояния в области этой точки проводят элементарный параллелепипед, грани которого стремятся к нулю, т.е. этот параллелепипед все время сжимается и стремится обратиться в рассматриваемую точку. На гранях этого параллелепипеда будут действовать напряжения в зависимости от того, как расположен параллелепипед. На его гранях могут действовать либо только нормальные напряжения, либо только тангенциальные напряжения, или, наконец, те и другие напряжения.

Возьмем элементарный параллелепипед в области точки А и так его сориентируем, чтобы на его гранях действовали только нормальные напряжения (рис. 2).

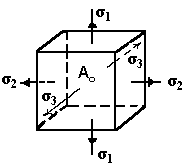рис. 2

Условимся называть его грани главными сечениями, а нормальные напряжения, действующие на главных площадках – главными напряжениями.

Таким образом, будем иметь три пары главных площадок и три главных напряжения σ₁, σ₂ и σ₃. Такое напряженное состояние, когда действуют три главных напряжения, называется объемным или трехосным.

Однако может быть такой случай, когда одно из главных напряжений обратится в нуль (σ₃ = 0), тогда будут действовать только два главных напряжения σ₁ и σ₂. Такое напряженное состояние называется плоским или двухосным (рис. 3).

рис. 3

Возможен и еще более простой случай, когда будем иметь только одно главное напряжение σ_{1 ,} остальные два σ₂ и σ₃ обратятся в нуль, такое напряженное состояние называется линейным (рис. 4).

рис. 4

Лучшим примером линейного напряженного состояния является простое растяжение или сжатие.

Нумерация главных напряжений производится не произвольно, а по следующему правилу. За первое главное напряжение (σ₁), принимают наибольшее по алгебраической величине, а за третье (σ₃) – наименьшее по алгебраической величине.

1.2. Линейное напряженное состояние

а) АНАЛИТИЧЕСКИЙ МЕТОД ОПРЕДЕЛЕНИЯ НАПРЯЖЕНИЙ

Возьмем брус, который подвергается растяжению, найдем напряжения в наклонном сечении под углом α к поперечному сечению (рис. 5).

рис. 5

Для этого проведем наклонное сечение, отбросим верхнюю часть бруса и приложим внутренние силы, которые должны уравновесить нагрузку Р (рис. 6).

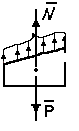рис. 6

Все внутренние силы приведутся к одной равнодействующей силе N, направленной в противоположную нагрузке Р сторону. Причем 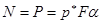N, где F_α – площадь наклонного сечения; р^* - полное напряжение в наклонном сечении.

Так как (где F – площадь поперечного сечения), то можем записать

, но 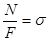(σ – напряжение в поперечном сечении), отсюда

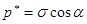[1]

Построив вектор полного напряжения р^* и разложивего вдоль внешней нормали к сечению и касательной к нему, получим нормальное напряжение в наклонном сечении σ_α и тангенциальное τ_α (рис. 7).

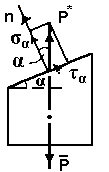рис. 7

Если угол α получается поворотом внешней нормали против часовой стрелки, его считают положительным, в противном случае он будет отрицательным.

Определим σ_α и τ_α :

;

Подставив в эти выражения значение р^* из формулы[1], получим:

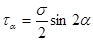[2]

Исследуя полученные выражения, найдем экстремальные значения σ_α и τ_α :

при α=0 σ_{α max}= σ cos²0⁰, т.е. σ_{α max} = σ,

Наибольшие нормальные напряжения действуют в поперечных сечениях;

при α=90⁰ σ_{α min}= σ cos²90⁰, т.е. σ_{α min} = 0,

Наименьшее значение, равное нулю, нормальные напряжения имеют в продольном сечении;

при α=45⁰ , т.е. ,

Наибольшее тангенциальное напряжение действует в наклонном сечении под углом 45⁰;

при α=0 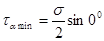, т.е.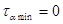

В поперечном сечении (α=0) тангенциальное напряжение отсутствует. А нормальные напряжения = σ_αmax. Это сечение является главным. Главное напряжение имеет максимальное значение. Во всех других сечениях нормальные напряжения будут меньше, чем в главном.

Условимся нормальное напряжение считать положительным, если направление его вектора совпадает с направлением внешней нормали – это растягивающее напряжение, в противном случае будем считать нормальное напряжение отрицательным – сжимающее напряжение.

Тангенциальное напряжение считают положительным, когда его вектор получается поворотом внешней нормали по направлению движения часовой стрелки, в противном случае оно будет отрицательным.

б) ГРАФИЧЕСКОЕ РЕШЕНИЕ (построение круга Мора)

Известно главное напряжение σ₁, равное напряжению в поперечном сечении при растяжении. Нужно определить напряжения в этой точке в наклонном сечении под углом α. Решить эту задачу надо графически.

Проводим оси координат. По оси абсцисс откладываем нормальные напряжения, а по оси ординат тангенциальные (рис. 8).

рис. 8

Отложим вдоль оси абсцисс значение главного напряжения σ в определенном масштабе. Получив отрезок ОА, разделим его пополам и из его середины (точка С) опишем окружность радиуса ОС=АС. Проведем из точки О луч под углом α с осью абсцисс до пересечения с окружностью (точка Д_α). Для нахождения координат σ_α и τ_α соединим центр окружности с точкой Д_α.

Из рис. 8 следует, что: ОК_α= ОС + СК_α, но 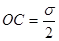, а из треугольника Д_αСК_α следует, чт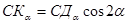о , но как радиус круга, поэтому:

.

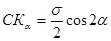Угол Д_αСК_α как внешний угол треугольника ОСД_α равен сумме внутренних несмежных с ним углов, т.е. равен 2α.

Подставив полученные значения отрезков ОС и СК_α в выражение для ОК_α, получим: или

Окончательно получим , а

Сравнив эти выражения, замечаем, что абсцисса точки в определенном масштабе равна нормальному напряжению в наклонной площадке, т.е. .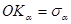

Из треугольника СД_α К_α следует, что Д_α К_α = CД_α sin2α, но , поэтому , а .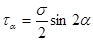

Отсюда следует, что ордината точки Д_α в определенном масштабе равна тангенциальному напряжению в наклонной площадке, т.е. .

Таким образом, координаты точки Д_α дают нам значения напряжений, действующих в наклонной площадке под углом α. При помощи построенного круга, называемого кругом напряжения, можно определить напряжения во всех сечениях, проведенных через рассматриваемую точку, т.е. круг определяет напряженное состояние в точке. Этот метод был предложен немецким исследователем Мором, и поэтому часто круг напряжений называют кругом Мора.

в) ЗАКОН ПАРНОСТИ КАСАТЕЛЬНЫХ НАПРЯЖЕНИЙ

Определим нормальные и касательные напряжения на двух взаимно перпендикулярных площадках.

Для площадки, наклоненной под углом α, по формуле [2] имеем:

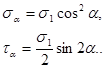
Для взаимно перпендикулярной площадки при значении угла нормальные и касательные напряжения можно определить или непосредственно из условия равновесия верхней или нижней части стержня (рис. 9), или по формулам [2] с заменой α на .

Применяя формулы [2], получим:

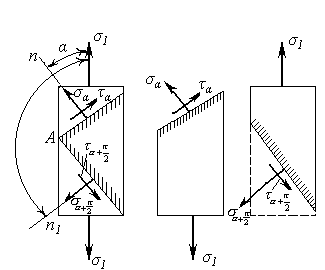рис. 9

Анализируя полученные результаты, видим, что, во-первых,

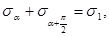
т.е. сумма нормальных напряжений по двум взаимно перпендикулярным площадкам постоянна и равна главному напряжению; во-вторых,

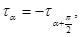
т.е. на двух взаимно перпендикулярных площадках действуют равные по величине и обратные по знаку касательные напряжения (закон парности или взаимности касательных напряжений). При этом касательные напряжения на двух взаимно перпендикулярных площадках направлены оба либо к ребру пересечения площадок, либо от ребра, как на рис. 9.

Например, если изменить знак σ, то напряжения и 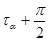изменят свое направление на противоположное и будут оба направлены к ребру А пересечения площадок.

Закон парности (взаимности) касательных напряжений имеет силу не только для одноосного, но и для любого другого напряженного состояния: двухосного и объемного.

1.3. Напряжения в наклонных сечениях при растяжении (сжатии) по двум взаимно перпендикулярным направлениям

а) АНАЛИТИЧЕСКИЙ МЕТОД РЕШЕНИЯ

Рассмотрим более общий случай плоского (двухосного) напряженного состояния, когда отличны от нуля два главных напряжения σ₁ и σ₂ (рис. 10а).

рис. 10

Как уже было отмечено ранее, индексы у обозначений главных напряжений ставятся так, что соблюдается неравенство σ₁ > σ₂, положительный угол α между направлением σ₁ и нормалью к произвольной площадке будем отсчитывать против часовой стрелки.

Между направлением напряжения σ₂ и площадкой угол равен .

Напряжения σ_α и τ_α в произвольном наклонном сечении можно или определить из условий равновесия трехгранной призмы АВС (рис. 10б), или вычислить по формулам [2], суммируя напряжения от действия σ₁ с напряжениями от действия σ₂ (при замене угла α на угол ).

В результате получим откуда

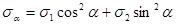[3]

Далее 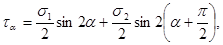откуда

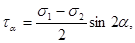[4]

Из формулы 4 видно, что максимальные касательные напряжения равны полуразности главных напряжений

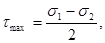[5]

и имеют место в сечениях, наклоненных под одним и тем же углом к направлениям σ₁ и σ₂, т.е. при α=45˚. Это следует из условия, что τ_max соответствует sin 2α=1.

Определив касательные напряжения на площадке, перпендикулярной к площадке АВ, убедимся, что и для двухосного напряженного состояния сохраняет свою силу закон парности касательных напряжений. В этом можно убедиться также по формуле [4], определив по ней значения и .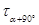

Частные случаи

1-й случай. Рассмотрим напряженное состояние, при котором σ₁= σ₂= σ (рис. 10в).

в этом случае на всех площадках, проходящих через исследуемую точку, касательное напряжение равно нулю, а нормальное напряжение имеет одно и то же значение σ_α = σ (см. формулы [3] и [4]). Такое напряженное состояние называется равномерным двухосным растяжением (или сжатием).

2-й случай. Рассмотрим напряженное состояние, представленное на рис. 10г, характеризующееся главными напряжениями σ₁= σ и σ₃= - σ. При этом σ₂= 0.

Определим напряжения в сечениях, одинаково наклоненных к направлениям σ₁ и σ_3, т.е. при α=45^˚ и α=135^˚ .

По формулам [3] и [4] получим σ_α = 0; =±σ. Такое напряженное состояние называется чистым сдвигом.

б) ГРАФИЧЕСКИЙ МЕТОД ОПРЕДЕЛЕНИЯ НАПРЯЖЕНИЙ ПРИ ПЛОСКОМ НАПРЯЖЕННОМ СОСТОЯНИИ

Пусть известны главные напряжения σ₁ и σ₂, требуется определить напряжения на площадке под углом α. Проведем координатные оси. По оси абсцисс отложим главные напряжения σ₁ и σ₂ (рис. 11), получим отрезки ОА и ОВ. Отрезок АВ разделим пополам, получим точку С. Точку С примем за центр круга, и опишем его радиусом СА = СВ.

рис. 11

Из точки В проведем луч под заданным углом α к оси абсцисс до пересечения с кругом, найдем координаты точки пересечения луча с кругом Д_α.

Из рис. 11 следует: ОК_α = ОВ + ВС + СК_α;

Подставив полученные значения отрезков ОВ, ВС и СК_α в выражение для отрезка ОК_α, получим:

После преобразований получим

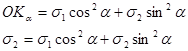
Сравнив приведенные выше выражения, приходим к выводу, что абсцисса точки Д_α представляет нормальное напряжение на наклонной площадке, т.е. .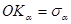

Найдем ординату точки Д_α . Из треугольника Д_α СК_α следует:

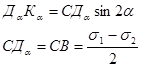
поэтому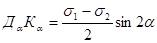

так как , то

Таким образом, ордината точки Д_α выражает тангенциальное напряжение на наклонной площадке .

Для определения напряжений на перпендикулярной площадке к данной, строим двойной угол (2β=180^˚+2α), путем продолжения радиуса СД_α до пересечения с кругом получаем точку Д_β, координаты которой и есть напряжения на этой площадке.

Таким образом, координаты любой точки круга дают напряжения на наклонных площадках, т.е. круг определяет напряженное состояние в данной точке.

1.4. Определение главных напряжений и положения главных площадок при плоском напряженном состоянии

а) АНАЛИТИЧЕСКИЙ СПОСОБ ОПРЕДЕЛЕНИЯ

Данная задача обратна предыдущей. Теперь известны нормальные и касательные напряжения, действуя по граням элемента (рис. 12.а). требуется определить положение главных площадок (угол φ) и величину главных напряжений (σ_max и σ_min). Рассмотрим равновесие трехгранной призмы с основанием АВС (рис. 12.б). Примем, что σ_α>σ_β. Угол φ будем отсчитывать от направления большего напряжения до нормали к площадке. За положительное направление отсчетов угла φ примем направление против часовой стрелки.

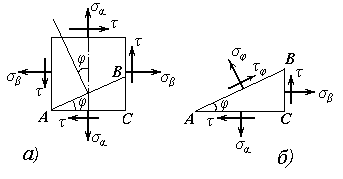рис. 12

Площадь наклонной грани обозначим через dF. Тогда площадь вертикальной грани будет dF sin φ, а горизонтальной - dF cos φ.

Проектируя все силы на направление σ_φ, получим

Проектируем теперь все силы на направления τ_φ

Сократив на dF и введя функции двойных углов, получим:

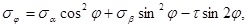[6]

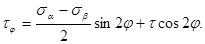[7]

При изменении угла наклона площадки φ величина σ_φ будет непрерывно изменяться.

Чтобы отыскать положения главных площадок, т.е. площадок, на которых действуют экстремальные нормальные напряжения, следует либо приравнять нулю производную , либо приравнять нулю касательные напряжения τ_φ, так как на главных площадках касательных напряжений нет.

В обоих случаях получаем следующую зависимость для определения угла φ₀ наклона главных площадок:

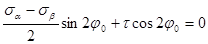
или

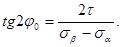[8]

Для получения экстремальных значений нормальных напряжений, т.е. величин главных напряжений, значение угла из формулы [8] подставим в формулу [6]. Предварительно тригонометрические функции в формуле [6] следует выразить через тангенс двойного угла. Для этого используют известные формулы тригонометрии:

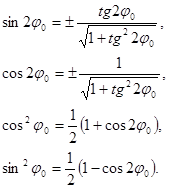
После несложных преобразований, которые необходимо сделать учащемуся самостоятельно, получим следующую формулу для определения величин главных напряжений

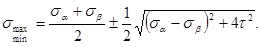[9]

Если одно из заданных нормальных напряжений равно нулю, то формула [9] упростится и примет вид

[10]

Этой формулой будем пользоваться в дальнейшем при изучении изгиба и сложного сопротивления.

Исследуя вторую производную 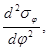можно убедиться, что на главной площадке под углом φ₀ при принятых условиях (σ_α > σ_β) действует максимальное главное напряжение, а на площадке под углом φ₀ +90^˚ действует минимальное главное напряжение.

Пример. Определить величину и направление главных напряжений в случае напряженного состояния, показанного на рис. 13.1.

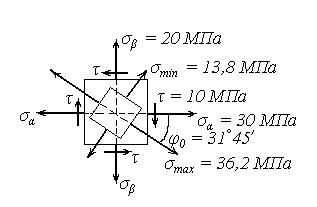рис. 13

Р е ш е н и е. По формуле [8] определяем положение главных площадок, перпендикулярных плоскости чертежа

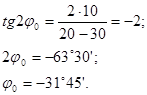
Знак «минус» показывает, что φ₀ отсчитывается от направления σ_α=30 мПа по часовой стрелке.

По формуле [9] получим:

В соответствии со сказанным выше σ_max действует на площадке под углом φ₀, σ_min – на площадке под углом φ₀ + 90^˚.

б) ОПРЕДЕЛЕНИЕ ГЛАВНЫХ НАПРЯЖЕНИЙ ГРАФИЧЕСКИМ МЕТОДОМ

При известных σ_α, σ_β и τ_α необходимо графически определить направление и величину σ_max = σ₁ и σ_min = σ_3. Графическое построение (рис. 14.1).

Принимаем масштаб напряжений. Проводим оси прямоугольной системы координат. Отложим на оси нормальных напряжений σ_α = OK_α и σ_β = OK_β. Восстанавливаем перпендикуляры к оси σ, отложив на них отрезки К_αД_α = τ_α и К_βД_β = τ_β (направление τ_α и τ_β принимаются в зависимости от знаков напряжений). Соединив точки Д_α и Д_β, получаем центр С круга Мора. Радиусом С Д_α или С Д_β описываем окружность, пересечение которой с осью нормальных напряжений дает точку А и В. Тогда ОА=σ₁ и ОВ= σ₃. Чтобы получить направление 1-го и 2-го главных напряжений на круге Мора, необходимо воспользоваться полюсом М.

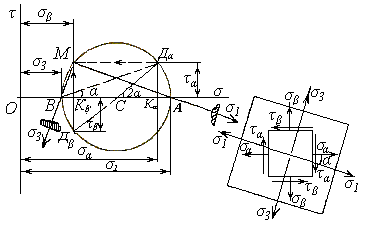рис. 14

1.5. Зависимость между деформациями и напряжениями при плоском напряженном состоянии. Удельная работа деформации.

Пусть брус прямоугольного сечения (рис. 15) растягивается по двум взаимно перпендикулярным направлениям х и у напряжениями σ₁ и σ₂. Определим относительные удлинения, которые получит брус в направлениях осей х, у и z.

рис. 15

Если бы на брус действовало одно растягивающее напряжение σ₁, то относительное удлинение в направлении растяжения согласно закону Гука было бы равно а по осям у и z брус получил бы относительные укорочения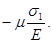

Аналогично этому при действии только одного растягивающего напряжения σ₂ относительное удлинение в направлении растяжения было бы равно а по осям х и z брус получил бы относительные укорочения

Следовательно, при одновременном действии напряжений σ₁ и σ₂ относительные деформации в направлениях осей х, у и z будут соответственно равны:

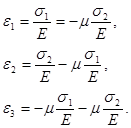
В общем случае объемного напряженного состояния относительные деформации ε₁, ε₂ и ε₃ соответственно будут равны:

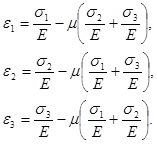[11]

Частные случаи. 1) Простое растяжение: σ₁= σ, σ₂= 0, σ₃=0; тогда по формуле [11] получим:

2) Растяжение по двум взаимно перпендикулярным направлениям, если σ₁= σ₂= σ; σ₃=0; тогда из формул [11] получим:

Если напряженное состояние плоское, т.е. σ₃=0, и известны относительные деформации ε₁ и ε₂, то из формул [11] легко определяются напряжения σ₁ и σ₂:

Этими формулами часто пользуются при экспериментальном определении напряжений, измеряя ε₁ и ε₂.

Найдем теперь выражение удельной работы деформации при растяжении или сжатии по двум направлениям. Удельная работа деформации при растяжении (сжатии) в одном направлении выражается формулой

[12]

При плоском напряженном состоянии, ориентируя грани кубика со стороной, равной единице, по площадкам, где действуют напряжения σ₁ и σ₂, получим:

Подставив сюда значения ε₁ и ε₂ из формул [11], при σ₃ = 0 будем иметь:

или

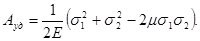[13]

Это и есть выражение удельной работы при плоском напряженном состоянии.

Пример. Определить относительные деформации бруса ε₁ и ε_2, если растягивающее напряжение σ₁ =60 МПа, а сжимающее σ₂ =- 75 МПа (рис. 16). Модуль упругости Е =2,2·10⁵ МПа. Коэффициент Пуассона μ=0,3.

Решение. На основании формул [11] имеем:

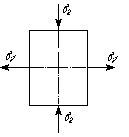рис. 16

Дата добавления: 2014-11-29