Аналіз і моделювання ризиків на основі функції корисності

Нехай виграш (дохід) представлений випадковою величиною Х і задана функція корисності .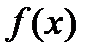

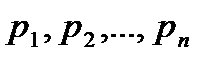Якщо Х приймає кінцеве число значень з ймовірностями , то математичне сподівання виграшу (очікуваний виграш 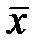) і математичне сподівання корисності (очікувана корисність 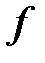) відповідно рівні:

; (4.28)

. (4.29)

У загальному випадку для безперервної випадкової величини 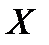з функцією щільності розподілу маємо:

;

.

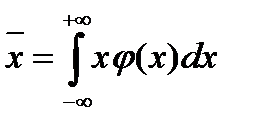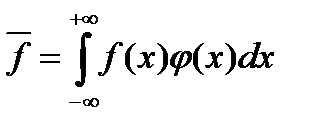Для встановлення взаємозв’язку між ризиком і функцією корисності використовується поняття детермінованого еквіваленту лотереї – гарантована сума 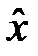, отримання якої еквівалентно участі у лотереї ( 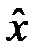~ G, тобто значення виграшу 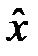гарантує особі таку ж корисність, як і участь у ризиковій лотереї). Детермінований еквівалент лотереї 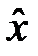визначається з рівняння:

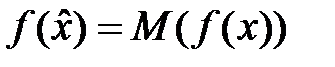. (4.30)

Сума, яку згідна уступити ОПР із середнього виграшу (доходу) з метою уникнення ризику, називається премією за ризик. Премія за ризик вимірюється в тих самих одиницях, що й випадкова величина , і для зростаючої функції корисності визначається як різниця між математичним сподіванням виграшу і детермінованим еквівалентом лотереї:

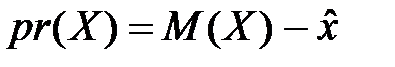. (4.31)

Очевидно, що інвестор, намагаючись уникати ризику, не погодиться брати участь у ризиковому проекті, якщо не матиме компенсаторів не тільки за використання своїх грошей, але і за ризик їх втратити - премії за ризик. Іншими словами, інвестор вимагає більш високої норми прибутку, якщо має місце ризик.

►Приклад 4.2. Нехай 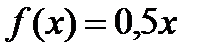і має місце лотерея 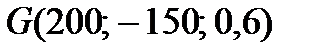. Знайти математичне сподівання виграшу, детермінований еквівалент лотереї і премію за ризик.

Користуючись (4.28) і (4.29), обчислюємо:

;

.

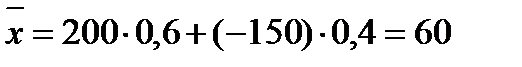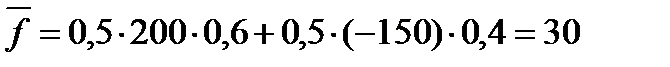З рівняння 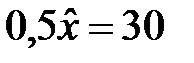знаходимо детермінований еквівалент лотереї: .

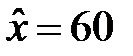Премія за ризик згідно (4.31) рівна:

.

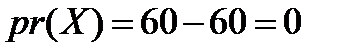Не важко переконатися, що для довільної лінійної функції корисності математичне сподівання виграшу і детермінований еквівалент лотереї співпадають, а премія за ризик рівна нулю. ◄

►Приклад 4.3. Знайти математичне сподівання виграшу, детермінований еквівалент лотереї і премію за ризик, якщо функція корисності має вигляд 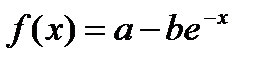, де і 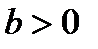, і ОПР має справу з лотереєю .

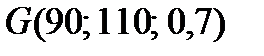Математичне сподівання виграшу рівне:

.

.

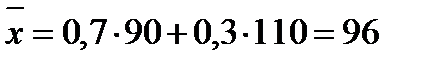Детермінований еквівалент лотереї знаходимо з рівняння

.

У результаті елементарних перетворень отримуємо таке значення детермінованого еквівалента лотереї:

.

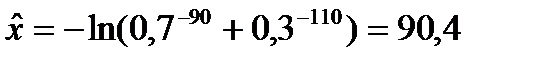Премія за ризик складає:

. ◄

Згідно основного положення теорії корисності, в умовах ризику ОПР керується рішенням, яке максимізує математичне сподівання корисності результатів.

Інформацію про ставлення ОПР до ризику надає функція корисності. У загальному випадку графік зростаючої функції корисності може бути трьох типів:

▪ кожна дуга кривої лежить вище своєї хорди – ОПР не схильна до друку;

▪ кожна дуга кривої лежить нижче своєї хорди – ОПР схильна до ризику;

▪ пряма лінія – ОПР нейтральна (байдужа) до ризику.

Графічну інтерпретація функцій корисності ОПР, не схильної і схильної до ризику, подано відповідно на рис.4.2 і рис.4.3, де

.

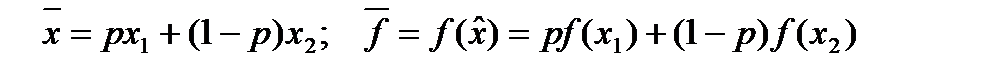ОПР вважають не схильною до ризику, якщо для неї можливість одержати гарантовано сподіваний виграш має вищий пріоритет за участь у лотереї:

. (4.31)

ОПР вважають схильною до ризику, якщо для неї більш пріоритетною є участь у лотереї, чим одержання гарантованого сподіваного виграшу:

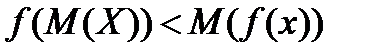. (4.32)

Нейтральність до ризику визначається байдужістю ОПР щодо вибору між отриманням гарантованої суми та участю у лотереї:

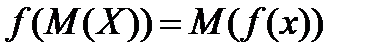. (4.33)

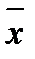
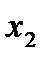
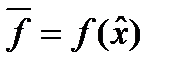
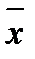
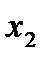
Рис.4.3. Функція корисності ОПР, схильної до ризику

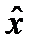
П

Рис.4.2. Функція корисності ОПР, не схильної до ризику

Премія за ризик є:

▪ додатною 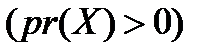для ОПР, не схильної до ризику;

▪ від’ємною для ОПР, схильної до ризику;

▪ рівною нулю 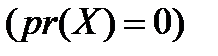для ОПР, нейтральної до ризику.

Представлені на рис.4.2 і 4.3 графіки функцій корисності не дають пояснення того факту, що особа в одних випадках демонструє схильність до ризику, а в інших намагається його уникнути.

Так, наприклад, реальною є поведінка особи, згідно якої вона схильна до ризику, пов’язаного з незначними сумами відносно великого достатку, та несхильність до ризику, пов’язаного з великими сумами. Графічна інтерпретація такої поведінки представлена на рис.4.4, а функції, які описують її, називаються функціями схильності – несхильності до ризику (С-НСР).

Аналітично функції С-НСР можна задати за допомогою зрізаних функцій розподілу ймовірностей:

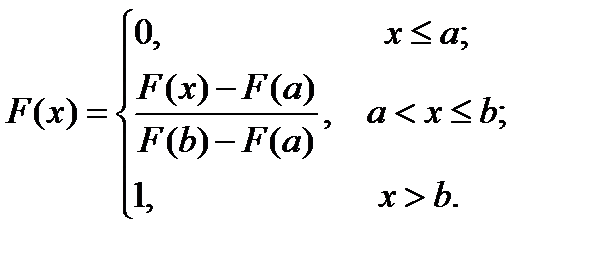(4.34)

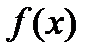
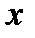
схильність до ризику

нейтраль-нітсь

несхильність до ризику

Рис.4.4. Функція схильності – несхильності до ризику

Для нормального закону розподілу з параметрами 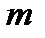і (математичне сподівання і середньоквадратичне відхилення) маємо:

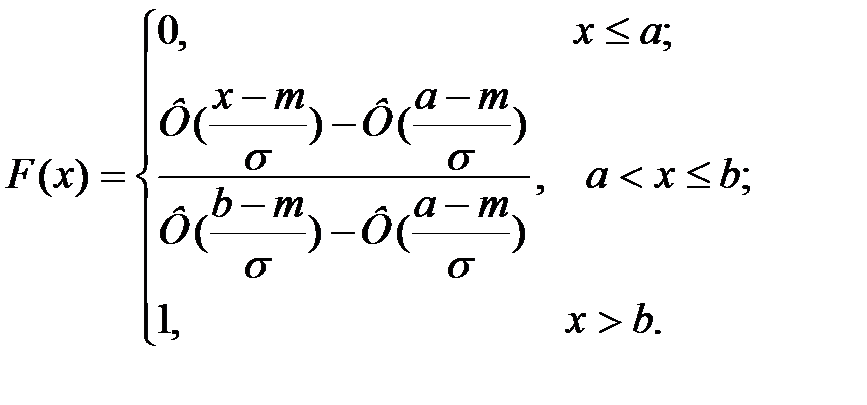
Лотерея з неперервним розподілом ймовірностей може бути записана таким чином:

,

де 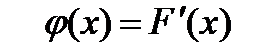, а - функція розподілу ймовірностей (функція С-НСР).

► Приклад 4.4. Особа має три альтернативні варіанти щодо вибору місця праці:

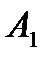▪ - місце праці зі стабільним доходом у розмірі 680 гр.од.;

▪ - місце праці, пов’язане із ризиком: дохід 600 гр.од. з ймовірністю і дохід 800 гр.од. з ймовірністю ;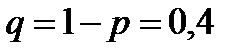

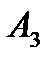▪ - місце праці, пов’язане із ризиком: дохід 470 гр.од. з ймовірністю і дохід 890 гр.од. з ймовірністю .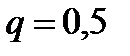

Визначити, яке місце праці обрати особі, якщо її функція корисності є зрізаним на проміжку [400; 1400] нормальним законом розподілу з параметрами і .

Згідно умови задачі функція корисності має вигляд:

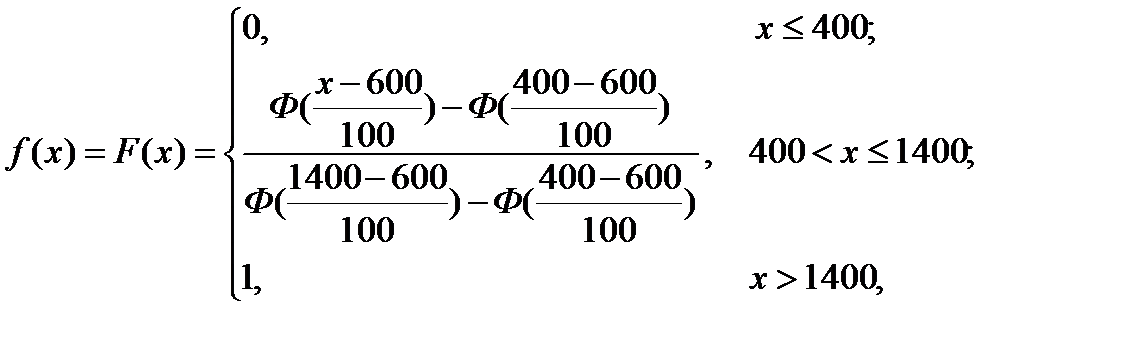
або

Вибору місця роботи 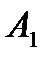відповідає вироджена лотерея

,

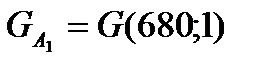корисність якої рівна

.

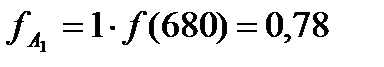Вибір другого місця роботи пов'язаний із лотереєю

.

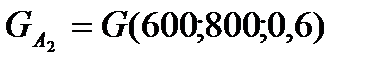Математичне сподівання доходу для лотереї :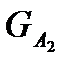

(гр.од.).

Математичне сподівання корисності лотереї :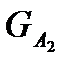

.

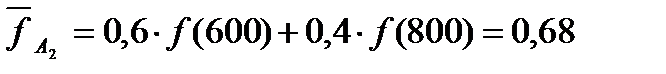Вибору третього місця роботи відповідає лотерея

.

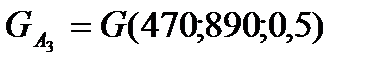Математичне сподівання доходу і корисності для лотереї 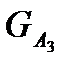відповідно рівні:

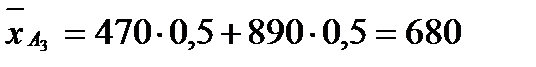(гр.од.).

.

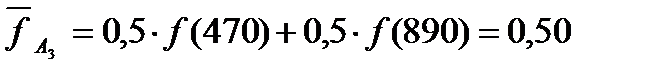Згідно отриманих результатів можна прийти до висновку, що кращим варіантом є вибір місця праці 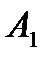, так як математичне сподівання доходів для всіх місць праці є однаковим (680 гр.од.), а найбільша корисність - . ◄

Дата добавления: 2014-11-29