
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Определенный интеграл. Основные свойства неопределенного интеграла
|
|
|
|
Основные свойства неопределенного интеграла
Неопределенный интеграл
Основные теоретические сведения.
1. Неопределенным интегралом функции f (x) называется множество всех ее первообразных F (x) + C и обозначается символом  , где функция F (x) называется первообразной функции f (x):
, где функция F (x) называется первообразной функции f (x): 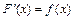 .
.
2. 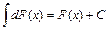 . 3.
. 3. 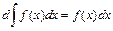 .
.
4.  . 5.
. 5. 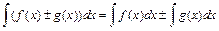 .
.
6. Если  , то
, то 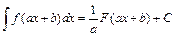 .
.
Таблица интегралов
7. 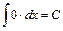 . 8.
. 8. 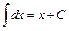 .
.
9. 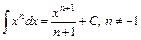 . 10.
. 10. 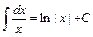 .
.
11. 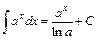 . 12.
. 12. 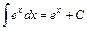 .
.
13. 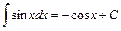 . 14.
. 14. 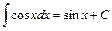 .
.
15. 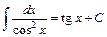 . 16.
. 16. 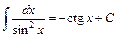 .
.
17.  . 18.
. 18. 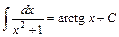 .
.
19.  . 20.
. 20. 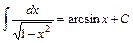 .
.
21. 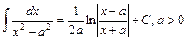 . 22.
. 22. 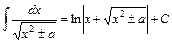 .
.
23. 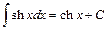 . 24.
. 24. 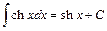 .
.
25. Теорема о замене переменной в неопределенном интеграле: пусть требуется найти интеграл от сложной функции вида 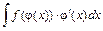 , тогда если заменой
, тогда если заменой 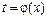 ,
, 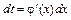 интеграл сводится к табличному
интеграл сводится к табличному 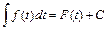 , то справедлива формула
, то справедлива формула 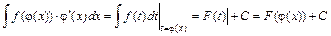 .
.
26. Формула интегрирования по частям: 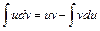 .
.
27. Некоторые интегралы, вычисляемые по частям:
| 1-я группа | 2-я группа | ||||
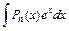
| u = Pn (x) | 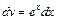
| 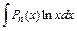
| 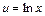
| dv = Pn (x) |
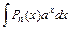
| 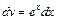
| 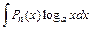
| 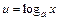
| ||
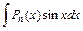
| 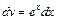
| 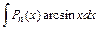
| 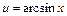
| ||
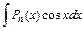
| 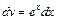
| 
| 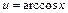
| ||
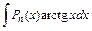
| 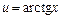
| ||||

| 
|
3-я группа: 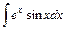 ,
, 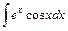 ,
,  ,
, 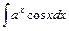 ,
, 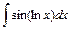 ,
, 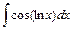 ,
, 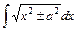 ,
, 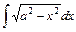 и др.
и др.
1. Пусть на отрезке [ a; b ] задана функция f (x). Произвольным образом разобьем отрезок [ a; b ] на n частей точками a = x 0 < x 1 < x 2 < … <
< xk –1 < xk < … < xn = b. Обозначим через D xk = xk – xk –1 – длину k -го отрезка. На каждом отрезке [ xk –1; xk ] возьмем произвольно точку x k и вычислим в ней значение функции f (x k). Найдем все произведения f (x k)D xk и составим интегральную сумму  . Если существует конечный предел интегральной суммы при n → ¥, не зависящий ни от способа разбиения отрезка [ a; b ] на части, ни от выбора точек x k, то этот предел называется определенным интегралом от функции f (x) на отрезке [ a; b ] и обозначается символом
. Если существует конечный предел интегральной суммы при n → ¥, не зависящий ни от способа разбиения отрезка [ a; b ] на части, ни от выбора точек x k, то этот предел называется определенным интегралом от функции f (x) на отрезке [ a; b ] и обозначается символом 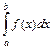 .
.
2.  – формула Ньютона-Лейбница.
– формула Ньютона-Лейбница.
3.  – формула интегрирования по частям.
– формула интегрирования по частям.
4. Геометрический смысл определенного интеграла: интеграл 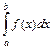 численно равен площади криволинейной трапеции, ограниченной слева и справа прямыми
численно равен площади криволинейной трапеции, ограниченной слева и справа прямыми 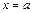 и
и 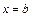 , осью
, осью 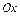 и сверху графиком функции
и сверху графиком функции  (рис. 8).
(рис. 8).
|
|
|

Рис. 8 Рис. 9
Приложения определенного интеграла в геометрии
5. Площадь криволинейной трапеции в декартовой прямоугольной системе координат (рис. 8) вычисляется по формуле: 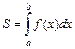 . Если
. Если 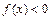 на
на 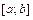 (график функции лежит ниже оси
(график функции лежит ниже оси 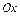 ), то
), то 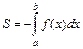 .
.
6. Если криволинейная трапеция ограничена сверху кривой, заданной параметрически  то площадь фигуры равна:
то площадь фигуры равна: 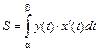 , где
, где 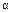 и
и 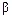 соответствуют значениям
соответствуют значениям 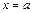 и
и 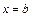 .
.
7. Площадь криволинейного сектора, ограниченного кривой 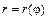 и двумя лучами
и двумя лучами 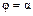 и
и 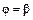 в полярных координатах (рис. 9) вычисляется по формуле:
в полярных координатах (рис. 9) вычисляется по формуле: 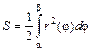 .
.
8. Если кривая задана уравнением  в декартовой прямоугольной системе координат, то длина этой кривой от точки
в декартовой прямоугольной системе координат, то длина этой кривой от точки 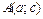 до точки
до точки 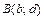 вычисляется по формуле:
вычисляется по формуле: 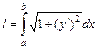 . Если кривая
. Если кривая  определяется уравнением
определяется уравнением 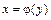 , то
, то 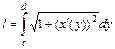 .
.
9. Если кривая задана параметрически  , то длина кривой
, то длина кривой  вычисляется по формуле:
вычисляется по формуле:  , где
, где 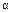 и
и 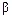 соответствуют значениям
соответствуют значениям 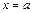 и
и 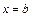 .
.
10. Если кривая задана уравнением 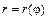 в полярных координатах, то ее длина между лучами
в полярных координатах, то ее длина между лучами 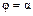 и
и 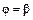 равна:
равна:  .
.
11. Объем тела, образованного вращением вокруг оси 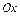 криволинейной трапеции (рис. 8), вычисляется по формуле:
криволинейной трапеции (рис. 8), вычисляется по формуле: 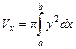 . Если эту криволинейную трапецию вращать вокруг оси
. Если эту криволинейную трапецию вращать вокруг оси 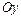 , то объем тела вращения равен
, то объем тела вращения равен 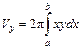 , причем
, причем  .
.
12. Если криволинейная трапеция ограничена кривой 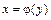 (
(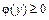 ), осью
), осью 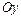 и прямыми
и прямыми 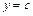 и
и  (рис. 10), то объем полученного тела вращения вокруг оси
(рис. 10), то объем полученного тела вращения вокруг оси 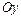 равен:
равен: 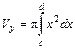 .
.
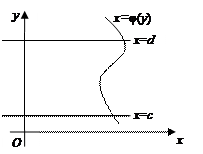 |
Рис. 10
13. Если дуга кривой, заданная в декартовых прямоугольных координатах  , где
, где 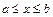 , вращается вокруг оси
, вращается вокруг оси 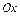 , то площадь поверхности вращения вычисляется по формуле:
, то площадь поверхности вращения вычисляется по формуле: 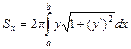 .
.
14. Если дуга кривой  , где
, где 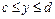 вращается вокруг оси
вращается вокруг оси 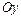 , то площадь поверхности вращения вычисляется по формуле:
, то площадь поверхности вращения вычисляется по формуле: 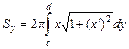 .
.
15. Если дуга кривой задана параметрически  где
где 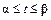 , то площадь поверхности вращения вокруг оси
, то площадь поверхности вращения вокруг оси 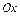 равна:
равна:  .
.
16. Если дуга задана в полярных координатах 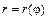 , где
, где 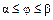 , то
, то  .
.
|
|
|
|
|
Дата добавления: 2014-11-29; Просмотров: 356; Нарушение авторских прав?; Мы поможем в написании вашей работы!