Арифметика рядов Фибоначчи 1 страница

Изучая размножение кроликов, итальянский математик Леонардо Пизано (по прозвищу Фибоначчи) с удивлением обнаружил, что оно происходит не хаотичным образом. Оно создает удивительный порядок чисел, последовательное сложение которых (начиная с двух наименьших чисел натурального ряда 1 и 1, или 1 и 2) выводит образовавшуюся бесконечную последовательность на такое отношение двух соседних чисел, которое стремится к золотому числу и тем ближе, чем это отношение дальше от начала ряда [24]. Приведем начало ряда:

Ряд 1.

…

…

Если теперь делить, например десятое число на одиннадцатое, то в результате получаем:

55: 89 = 0,617977528,

что только на 5,646×10^-5 меньше золотого числа 1/ Ф = 0,618033988…. Если же разделить одиннадцатое число на десятое имеем:

89: 55 = 1,618181818,

что на 1,478295×10^-4 больше золотого числа Ф = 1,618033988, то есть результат равен золотому числу по четырем знакам, чего достаточно для большинства практических целей. Результат же от деления, например двадцать первого числа на двадцатое дает точность золотого числа

17711: 10946 = 1,618033985,

до девятого знака, т.е. такую точность, которая не нужна в практике.

Аналогичный ряд был получен математиком Люка, только у него первые два числа равнялись 1 и 3. Посмотрим, на примере тех же членов ряда Люка, как они приближаются к золотому числу (ряд 2).

Ряд 2.

…

…

Делим десятое число на одиннадцатое и получаем:

123: 199 = 0,61809045,

истинное значение – Ф = 0,61803399…

Делим одиннадцатое число на десятое:

199: 123 = 1,617886179, истинное значение – Ф = 1,61803399…, то есть те же четыре знака точности. Делим двадцать первое число на двадцатое:

39601: 24475 = 1,618018386.

Приближение к золотому числу чисел Люка происходит несколько медленнее, чем ряда Фибоначчи, но и этого для практических целей достаточно. Отметим, что приближение это начинается с двух величин, одна из которых больше Ф, а другая меньше ее, и идет с чередованием как со стороны, превышающей Ф так и от величин, меньших Ф. Отметим это очень важное обстоятельство для понимания рядов.

Теперь посмотрим, что происходит с любыми двумя случайными числами “построенными” в ряд, аналогичный ряду Фибоначчи, например, с числом 7 и большим по числовой значимости числом 16 (ряд 3).

Ряд 3.

											…
											…
…
…

И проделаем те же расчеты, которые производились ранее. Делим десятое число на одиннадцатое, а потом одиннадцатое на десятое:

691:1118 = 0,6180679,

1118: 691 = 1,6179450,

и двадцать первое на двадцатое:

137507: 84984 = 1,618033983,

получаем результаты аналогичные ранее проведенным расчетам и с примерно той же точностью.

Попробуем произвести еще один расчет. Сведем в один ряд маленькое дробное число и большое, например, 0,25 и 844,05 (ряд 4).

Ряд 4.

0,25	844,05	844,3	1688,35	2532,65		6753,65	10974,6	17728,	28702,9
	…							…
46431,2	…							…

И еще раз проделаем расчеты с числами из тех же столбцов:

28702,95: 46431,25 = 0,61818172,

46431,25: 28702,95 = 1,61747315,

и делением двадцать первого числа на двадцатое:

9240662: 5711043 = 1,618034044.

Примерно те же точности, что и в предыдущих примерах, а это означает, что ряды типа Фибоначчи и Люка появляются не только при использовании первых трех чисел натурального ряда, но и при употреблении двух любых арифметических величин. И, похоже, во всех случаях на одиннадцатой операции сложения пропорция из двух соседних чисел будет обусловливать получение золотого числа с точностью до четвертого знака.

Продолжим рассмотрение ряда Фибоначчи, например, с восемнадцатого числа и попробуем понять, к чему стремятся получаемые члены ряда. Заполним ряд 5-й.

Ряд 5.

Разделим все члены пятого ряда на какое-то число из них, например, на двадцать пятое и полученный результат запишем в шестой ряд.

Ряд 6.

0,034	0,0557	0,0902	0,146	0,236	0,382	0,61803	1,000	1,61803	2,6180	4,2360

Выясняется, что члены ряда Фибоначчи, начиная примерно с 12 слагаемого представляют собой геометрическую прогрессию, основанием которой является золотое число Ф, умноженное на некоторый коэффициент, которым может оказаться любое слагаемое ряда (например, двадцать первое 17711 или двадцать пятое 121393 в ряду 5 и т.д.). В результате деления членов ряда 5 на 121393 были найдены и занесены в 6 ряд золотые числа греческого ряда, которые получаются в настоящее время последовательным делением единицы на Ф (нисходящий ряд) и последовательным умножением единицы на Ф (восходящий ряд). Из ряда 6 следует, что все ряды геометрической прогрессии в неявной форме включают золотое число Ф, никогда не начинаются с некоторого числа и бесконечны как в сторону восхождения, так и в сторону нисхождения. Центром же их является базисная 1. Однако ряды типа Фибоначчи имеют началом “случайные” величины и только на одиннадцатой операции сложения начинают изменять свое первоначальное качество, переходя с ряда слагаемых в геометрическую прогрессию, создавая тем самым новое качество – геометрическую прогрессию.

И можно полагать, что физическая сущность рядов Фибоначчи заключается в некотором моменте различия между исходными величинами слагаемых, и это различие прослеживается на протяжении всего процесса суммирования в виде бесконечного стремления изначально суммируемых чисел к золотому числу Ф.

Однако вернемся к рядам. Несколько позже другой ученый, французский математик Б. Паскаль, изучая процесс деления клетки, обнаружил, что оно происходит путем раздвоения материнской клетки, а каждая последующая клетка тоже делится пополам, образуя геометрическую прогрессию. В симметричном же построении цифр столбцом друг под другом, проявляется что-то подобное треугольнику: 1; 2; 4; 8; 16; … и т.д. Процесс получения геометрической прогрессии с цифры два был назван “треугольником Паскаля”. Интересно и очень значительно то, что именно этим способом разделяются на меньшие отрезки древнерусские соизмерительные инструменты – сажени. (Сажень, полсажени, четверть сажени – локоть, одна восьмая – пядь, одна шестнадцатая – пясть и последний отрезок, одна тридцать вторая – вершок). Архитектор А. Пилецкий [25]использовал систему удвоения и раздвоения русских саженей для построения в единой системе чисел нескольких рядов Фибоначчи. Т.е. сдвоил ряд Фибоначчи, изменив его качество и получив уже не один ряд, а как минимум два взаимосвязанных ряда, числа, которых стали таблицей. Поэтому два и более ряда типа Фибоначчи можно назвать рядом Пилецкого. Построим таблицу 3 по его методу.

В этой таблице 3 третий снизу ряд чисел – Фибоначчи (отмечен полужирным шрифтом). Из него следует, что он начинается одной единицей, а не двумя, как сегодня принято. Все члены поля получаются по рядам последовательным сложением двух соседних чисел, т.е. методом Фибоначчи, а столбцы – удвоением каждого нижнего числа, т.е. методом Паскаля. В результате все числа таблицы

Таблица 3.

										…
…	…	…	…	…	…	…	…	…	…	…
										…
										…
										…
										…
0,5		1,5	2,5		6,5	10,5		27,5	22,5	…
0,25	0,5	0,75	1,25		3,25	5,25	8,5	13,25	22,25	…
…	…	…	…	…	…	…	…	…	…	…

оказываются связанными между собой коэффициентами и по горизонтали (по строкам) и по вертикали (по столбцам), и по диагоналям. Эта связь, которая ощущается в начале таблицы достаточно зыбко, все “упрочняется” по мере возрастания чисел и, наконец, превращает таблицу в матрицу, бесконечную в трех направлениях, все члены которой связаны между собой и как бы постоянно “помнят” об этой связи, “помнят” о своей матрице. Этой “памятью” обладают все вещественные числа. И им более подходит наименование “софистические” или “мудреные” числа, название которое им было дано итальянским математиком Кардана. Неисчислимая бесконечность матрицы как бы отображает непрекращающийся процесс наращивания числового поля, обусловливая динамический характер золотым целым, дробным и иррациональным числам.

“Вырежем” часть поля таблицы 3, начиная, например с двадцать первого числа и рассмотрим, какими коэффициентами (числами золотых пропорций) связываются числа этого поля (таблица 4). Для чего разделим все члены числового поля таблицы 4 на число 46368 (в таблице 4 выделено полужирным шрифтом) и, заполним аналогичную таблице 4 сетку получившимися числами с точностью до пятого знака. Образовавшаяся таблица приобретает свойства золотой матрицы (матрица 1)

Таблица 4

8855,5	14328,5		37512,5	60696,5
4427,75	7164,25		18756,25	30348,75

Матрица 1 есть фрагмент числового поля, относящегося к классу русских матриц, описанных в [26]. Это единственная бесконечная во всех направлениях золотая матрица, у которой члены среднего ряда повторяют греческий ряд золотых чисел, базисный столбец образуют целые четные числа Паскаля, а остальные числа поля пропорциональны золотому числу.

Матрица 1.

1,5279	2,4721		6,4721	10,472
0,76393	1,2361		3,2361	5,2361
0,38197	0,61803		1,61803	2,61803
0,19098	0,30902	0,5	0,80902	1,3090
0,09549	0,15451	0,25	0,40451	0,65451

Класс русских матриц единственный из числа матриц, в котором два любых числа по горизонтали при последовательном сложении образуют третье. Он – объемен и обладает множеством особенностей, отсутствующих у других матриц, но главное – он базируется на золотых пропорциях (о классе русских матриц далее). Матрица же 1 имеет следующие золотые коэффициенты взаимосвязи:

По столбцам – 2,

По строкам Ф = 1,618,

По диагонали слева направо снизу вверх 2 Ф = 1,618 × 2 = 3,236,

По диагонали слева направо сверху вниз 2/ Ф = 2/ 1,618 = 1,236.

Существует еще несколько способов нахождения золотого числа Ф. К ним относятся деление отрезка в крайнем и среднем отношении (далее рассматривается подробнее), представление Ф в виде цепной дроби, и представление его в радикалах. Рассмотрим вкратце эти методы. Начнем с цепной дроби. Ее запись:

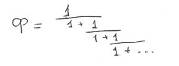
Если ограничить “спускающийся” ряд знаменателя двенадцатью членами и, приняв за последнее число 1, решить эту дробь, то решение начнется с числа 2 и приближение к Ф будет происходить чередуясь как “спуск” с величины большей золотого числа с 2, так и “подъем” с меньшей – 0,5, т.е. имеет осциллирующий характер. В результате на той же одиннадцатой операции будет получено число Ф с точностью до четвертого знака. То есть цепная последовательность приближения суммируемых единиц знаменателя к золотому числу повторяет суммирование чисел рядов Фибоначчи – Люка. Если же за последнее число знаменателя примем не 1, а, допустим, 16 или любое другое число, то расчеты показывают, что приближение идет с осциллирующим чередованием и то же количество операций. Таким образом процедура получения Ф по цепной дроби практически повторяет результаты решения по рядам Фибоначчи, только слагаемые числа находятся в знаменателе и не зависит от того, какое число заключает “цепной” знаменатель.

Коротко ознакомимся с нахождением числа Ф методом “радикалов”.

Понятно, что начальным в процедуре расчета или конечным в ряду радикалов является число 2. Подставляем его в радикал и проведя расчеты убеждаемся, что число Ф с точностью до четырех знаков получается на той же одиннадцатой операции, но приближение к нему идет только сверху. Проведем расчеты, поставив последним в ряду радикалов число 16. Результат полностью аналогичен предыдущему. Число Ф получается на одиннадцатой операции, приближение идет сверху. Таким образом все четыре способа нахождения числа Ф являются в какой-то мере аналогами. Отличие только в том, что метод сложения любых вещественных чисел обусловливает быстрое получение основного варианта золотой русской матрицы.

Здесь же отметим основные моменты свойств рядов Фибоначчи:

- Получение золотого числа Ф методом Фибоначчи – Люка не ограничивается сложением двух минимальных чисел 1 и 3, а распространяется на любую пару вещественных чисел.

- Золотое число Ф с точностью до четвертого знака включительно во всех случаях получается из соотношения двух соседних чисел ряда уже на одиннадцатой операции сложения. Количество операций сложения, необходимых для приближения к золотому числу, не определяется величиной слагаемых чисел.

- Последовательность приближения к Ф идет как сверху вниз (результат первого деления превышает Ф), так и снизу (результат первого деления меньше Ф), но, никогда не становится равным Ф, приближаясь к нему на бесконечно малую величину.

- Если известно одно число класса Фибоначчи, то имеется возможность получения всего потребного для операций ряда и тем точнее, чем далее оно находится от начала ряда. Числа “помнят” о своем месте в ряду.

- Важнейшим обстоятельством для понимания физического смысла золотой пропорции становится наличие только двух чисел, участвующих в построении ряда. Можно полагать, что эти числа математически отображают взаимосвязи реальных тел природы.

- Каждый ряд Фибоначчи, последовательно возрастая, «вырождается» в геометрическую прогрессию.

- Все ряды геометрической прогрессии в неявной форме включают золотое число Ф и бесконечны как в сторону восхождения, так и в сторону нисхождения.

- Применение геометрической прогрессии Паскаля к рядам Фибоначчи обусловливает появление таблиц с взаимосвязанными по всему полю числами.

- Геометрические прогрессии рядов Фибоначчи при делении всех чисел поля на одно из них образуют золотые объемные матрицы.

- Числовое поле русских матриц отображает высшую арифметическую и степенную комбинаторику как гармонию природных процессов, выраженную в математической форме.

Наличие формальных и природных свойств у чисел и алгебраических символов обусловливает возможность представления одних и тех же уравнений как в алгебраической, так и в геометрической форме. Именно этим методом решается задача деления отрезка в крайнем и среднем отношении.

3.2. Библейская геометрия

Золотого сечения

Есть у датского сказочника Андерсена изумительная сказка о гадком утенке.

На одном гомонливом птичьем дворе жил в семье «правильных» утят неприкаянный утенок. Он был безобразен, неповоротлив, чуден и презираем всем птичьим содомом. Он был одинок. Все его попытки присоединиться к какому-либо птичьему семейству заканчивались тем, что его отовсюду гнали, били, клевали. И так продолжалось до тех пор, пока «утенок» не превратился в белого красавца лебедя.

В математике существует свой гадкий «утенок» − золотая пропорция. И хотя к этой пропорции с давних пор проявлялся немалый интерес, интерес этот был односторонен и проявлялся в основном со стороны деятелей искусств: художников, скульпторов, историков, архитекторов. Ни одно направление математики, физики, и других точных наук не считало и не считает золотые пропорции своей частью или разделом. Пропорция эта оказалась на столетия не востребованной ни одним из предметов современной науки. Даже не смотря на то, что «утенок» − золотые пропорции на глазах превращается в «белого лебедя», необходимых всему спектру научных дисциплин. Мы полагаем, что «бесхозность» золотых пропорций канула в лету. Золотые пропорции – базис русской геометрии, основа отображения природных процессов в математике и физике, становятся обязательным элементом каждой научной дисциплины. Познакомимся с этим базисом.

Откуда пришли представления о делении отрезка в крайнем и среднем отношении, позволяющем получать золотое число Ф и образующее пропорцию, названную Леонардо да Винчи «Золотым сечением», а Кеплером «Божественной пропорцией» − неизвестно. Но в Древнем Египте и в Древней Греции на основе золотого числа Ф = 1,618… был получен ряд из 11 чисел посредством последовательного бесконечного умножения базисной 1 на Ф (восходящая ветвь ряда) и деления базисной 1 на Ф (нисходящая ветвь ряда), имеющий названия золотого ряда (варианты: греческий или египетский ряд [26]). Воспроизведем его:

…; 0,934; 0,056; 0,090; 0,146; 0,236; 0,382; 0,618: 1,00; 1,618; 2,618; 4,236; …

Золотое число Ф = 1,618... получается несколькими способами, один из которых - деление отрезка в крайнем и среднем отношении (рис. 42). Для чего отрезок делится в крайнем и среднем отношении и о чем свидетельствует золотое число Ф, до сих пор неизвестно. Известно только, что деление это создает эстетически законченный образ тех человеческих творений, в которых они находят применение. Отметим, что в постановке задачи говорится о делении одного отрезка на две неравные части а и с так (рис. 42), чтобы весь отрезок (а + с) относился к большей части с как с к меньшей части а. Для получения золотой пропорции отрезок АС делится на две неравные части АВ = а и ВС = с так чтобы его длина АС = АВ + ВС = (а + с) относилась к большей части с, как с относится к меньшей части а. Запишем это отношение и проведем несколько более сложные, чем ранее, расчеты:

А В С

а с

Рис. 42.

(а + с)/с = с/а (3.1)

Пропорция (3.1) носит название золотой пропорции. В данном случае подразумевается конечная в рациональных числах длина отрезка (а + с), кратная некоторому измерительному инструменту, допустим метру. В условии задачи нигде не говорится о невозможности его целочисленного или дробного рационального деления и о нерациональности двух (?)образующихся при делении отрезков. Это очень важная оговорка. Она подтверждает непреднамеренный, а как бы вероятностный или даже случайный характер деления. Проверим эту случайность, заменив в (3.1) отношение с/а на b:

b = с/а, (3.2)

и, подставив (3.2) в (3.1), получаем квадратное уравнение

b² - b - 1 = 0, (3.3)

решая его, находим два значения величины b:

b₁ = (1+Ö5)/2 = Ф = 1,6180339, (3.4)

b₂ = (1-Ö5)/2 = − 1/ Ф = − 0,6180339. (3.4)

Золотое число Ф − является числом иррациональным (скрытым от точности числом). То есть таким числом, бесконечная последовательность которого не может быть вычислена до конца, сколько бы времени его ни вычисляли. И для его получения приходится прерывать вычисления, округляя результат на той цифре, которая необходима по условиям задачи. А это означает, что иррациональное число, понимаемое нами как число фиксированное, таковым не является. Оно индивидуально, не имеет однозначного количественного выражения и отображает своего рода математическое качество (качества не складываются). Оно отражает неограниченную количественную величину и не может точно складываться как с рациональными, так и с иррациональными числами. Иррациональное число - это бесконечный процесс, который продолжается в формализации даже в том случае, когда мы прерываем вычисления. Прерывая вычисления, мы не прерываем процесса. И можно считать, что ряд золотых чисел есть отображение совокупности взаимозависимых, непрерывных процессов. Процессов, соответствующих многим формам движения природных систем. Оно квантованный (выделенный из числового ряда) элемент числового ряда, обособленный от него и не примыкающий ни к одному большему или меньшему числу. Все операции с ним проводятся с приблизительной точностью. Повторяем: иррациональное число - качественная индивидуальность, и, следовательно, бесконечный ряд иррациональных чисел не является дурной бесконечностью и не входит ни в один числовой ряд. С получением иррационального числа в математику входит представление о числовом математическом качестве и квантовании чисел, вне зависимости от того, осознали это ученые или нет. Квантованное иррациональное число - основа и предтеча квантованной геометрии. Но вернемся к Ф.

Получив Ф и ее обратную величину, т.е. два числа b₁ и b₂, мы успокаиваемся, так и не определив, чему же равны количественные величины чисел а и с в формуле (3.1) и какое отношение они имеют к b, тем более, что подстановка b в (3.2) не приводит к определению величин а и с, а следовательно, не решает поставленную задачу. Тогда зачем же мы находим b? Ответ - только для того, чтобы получитьбезразмерностное Ф, поскольку знаем, что это число - основа золотой пропорции и потому знание величины числового значения отрезков а и с нам уже не требуется. Но в чем же суть золотой пропорции?

Попробуем решить (3.1) другим путем. Умножим числитель и знаменатель левой части отношения (3.1) на а. А правой части на с и, сократив знаменатели, получим следующее уравнение:

Дата добавления: 2014-12-07