Нормальный закон распределения

Среди случайных величин особое место занимают нормальные случайные величины, подчиняются так называемому нормальному закону распределения:

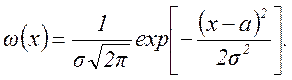(2.23)

Определим 1-й начальный момент нормальной случайной величины ξ:

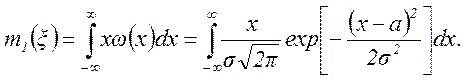
Сделав замену 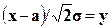, получим

так как первый из интегралов равен нулю в силу нечетности подынтегральной функции, а

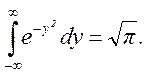
Итак, a=m₁(ξ).

Определим теперь 2-й центральный момент нормальной случайной величины ξ:

так как

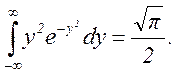
Таким образом, величины a и σ², полностью определяющие нормальный закон распределения, представляют собой соответственно среднее значение и дисперсию случайной величины ξ, т.е. нормальный закон распределения плотности определяется, если известны первые два момента. Из формулы (2.23) видно, что нормальное распределение симметрично относительно среднего значения случайной величины a. Максимум плотности вероятности,соответствующий x=a, равен

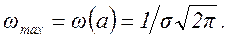
На рис 2.1 приведен вид нормального закона для различных σ при а=0.

Рис. 2.1

Нормальный закон распределения занимает особое положение в силу того, что большинство реальных случайных величин имеет распределение, близкое к нормальному. Последнее обстоятельство связано с тем, что на практике случайные величины обычно являются результатом совокупного действия многих независимых случайных факторов и, при некоторых условиях, по мере увеличения числа этих факторов закон распределения асимптотически приближается к нормальному. Условия эти определяются центральной предельной теоремой теории вероятности, которая в упрощенном виде может быть сформулирована следующим образом: если независимые случайные величины ξ₁, ξ₂, …, ξ_n имеют одинаковые распределения с конечной, отличной от нуля дисперсией σ², то при n→∞ сумма этих величин стремится к нормальному распределению со средним значением 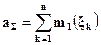и дисперсией .

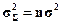А. М. Ляпунов показал, что тенденция к нормализации случайных величин имеет место и при более общих предположениях.

Рис. 2.2

Решение многих практических задач не столь критично к точности аппроксимации закона распределения и уже в случае, когда случайная величина определяется несколькими примерно равноценными независимыми факторами, закон ее распределения можно приближенно аппроксимировать нормальным законом.

Интегральный закон распределения, соответствующий нормальному закону (2.23), имеет вид:

(2.24)

Если перейти к нормированным отклонениям , то получим

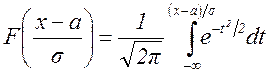(2.25)

Функция 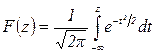, представляющая собой вероятность того, что нормированное случайное отклонение не превзойдет величину z, называется интегралом вероятности. Вид этой функции приведен на рис. 2.2.

Поскольку

то F(-z)=1-F(z) и функцию F(z) достаточно определить в положительной области.

Вероятность того, что нормальная случайная величина ξ не выйдет за пределы интервала [x₁, x₂]

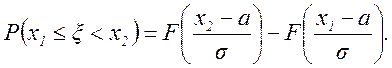(2.26)

Дата добавления: 2014-12-07