Уравнение второго порядка

Практически А(w) находится как отношение модулей числителя и знаменателя частотной передаточной функции W(jw).

Для рассматриваемого примера это даёт:

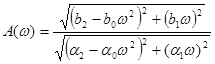
Функция y(w) находится как разность аргументов числителя и знаменателя W(jw). Для рассматриваемого примера:

.

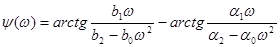Частотная передаточная функция получается из обычной передаточной функции простой заменой p=jw.

Системы с одной степенью свободы, это системы с сосредоточенными параметрами. Для них характерно наличие масс, которые считаются недеформируемыми и сосредоточенными в конечном числе точек.

Системы с бесконечно большим числом степеней свободы называются системами с распределенными параметрами. К ним относятся мембраны, струны, стержни и другие упругие тела.

Подвижная система с одной степенью свободы, т.е. система с сосредоточенными параметрами может быть описана дифференциальным уравнением 2-го порядка. К числу приборов описываемых такими уравнениями относятся: гироскопические вертикали, пружинные акселерометры с жидкостным демпфированием, гальванометры различных типов.

Для описания процессов, происходящих в системах с распределенными параметрами, применяют дифференциальные уравнения в частных производных с переменными коэффициентами.

Уравнение моментов системы с сосредоточенными параметрами рассмотрим на примере маятникового акселерометра.

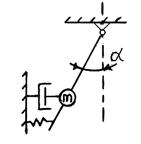
Рис. Схема маятникового акселерометра

Без учёта сил сухого трения уравнение имеет вид:

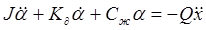
где J – момент инерции подвижной системы; К_¶ - коэффициент углового демпфирования; С_ж – угловая жесткость, а – угол отклонения маятника, x – перемещение объекта, на котором установлен акселерометр, вдоль оси его чувствительности. Q – параметр, определяющий возмущающие силы.

В том случае, если действует постоянное ускорение, то Q=ml, где l – расстояние от оси подвеса до центра тяжести маятника. При действии ускорения по гармоническому закону Q=mlsin(wt+j). Где j - сдвиг фазы между возмущающим воздействием и отклонением маятника. Следует обратить внимание на то, что размерность правой части уравнения соответствует размерности левой его части.

Рассуждения касаются именно маятниковых акселерометров т.е. приборов у которых чувствительная масса расположена на маятнике. Все дальнейшие выкладки будут справедливы и для осевых акселерометров у которых подвижная масса отклоняется возвратно – поступательно вдоль оси.

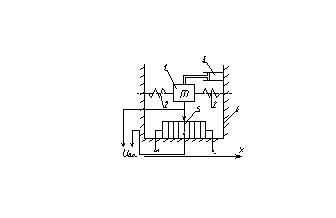
Здесь 1-подвижная масса, 2-пружины, 3-демпфер, 4-корпус, 5-потенциометр.

Однако в этом случае в уравнении следует произвести замену некоторых специфических составляющих величин, относящихся к угловому движению. При этом, уравнение будет иметь вид:

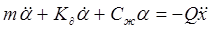
Здесь m – масса маятника, a - его перемещение, К_¶ - коэффициент линейного демпфирования; С_ж – жесткость пружины.

При постоянном ускорении Q=m, при изменяющемся по гармоническому закону Q=msin(wt+j).

Уравнение второго порядка необходимо для расчёта АЧХ и ФЧХ систем. В этом случае мы задаём амплитуду сигнала и рассчитываем характеристики при каждом значении w.

Если принять угол a за выходной сигнал, то передаточная функция прибора будет:

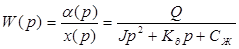(22)

Рассмотрим реакцию системы на ступенчатое воздействие x=А 1(t) при нулевых начальных условиях (t = 0, ).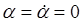

Характеристическое уравнение системы т.е. уравнение при отсутствие возмущающих сил:

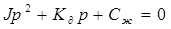
Это уравнение можно переписать:

р² + 2bр +w₀² = 0

где .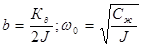

Параметр w₀ определяет круговую частоту собственных не демпфированных колебаний системы. Учитывая, что на собственную частоту не демпфированных колебаний углового маятникового акселерометра, расположенного вертикально, кроме жёсткости пружины влияет также составляющая силы тяжести, выражение для w₀ должно быть переписано в виде

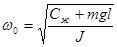
Отметим, что слагаемое mgl, как правило, существенно меньше жёсткости пружины.

Далее введем безразмерный коэффициент, называемый степенью успокоения:

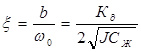
Величина степени успокоения существенно влияет на формы переходного процесса и частотных характеристик. Для определения переходной функции вначале решают характеристическое уравнение и находят его корни p₁ и p₂.

Характеристическое уравнение запишем в виде

P² + 2 xw₀ P + w₀² = 0.

Корни уравнения определим из выражения

р_{1, 2} = - xw₀ ± w₀ 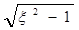(23)

Выражение для амплитуды колебаний системы, имеет вид:

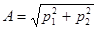
В общем случае вид переходного процесса системы 2-го порядка зависит от характера корней р₁, р₂ здесь могут быть три случая:

9.3.1 р₁ ¹ р₂. Корни не равны и действительны

Этот случай соответствует x>1.

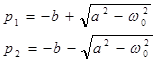
При этом переходная функция при p₁¹p₂:

(24)

Разделив (24) на установившееся значение , выражая р₁ и р₂ через w₀ и x в соответствии с (23) и заменяя w₀t=t, получим выражение переходной функции в безразмерной форме

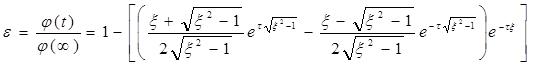
где t - безразмерное время.

Переходный процесс в системе второго порядка при x>1 и при нулевых начальных условиях имеет апериодический характер.

Динамическая ошибка системы равна

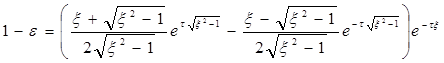
Теперь, если левую часть уравнения приравнять допустимой динамической ошибке D и решить уравнение относительно t, то получим безразмерную длительность переходного процесса.

Однако это уравнение не имеет явного решения относительно t, а возможно лишь численное решение задачи.

На рисунке показаны кривые переходных процессов в системе 2-го порядка. В таблице приведены значения безразмерной длительности переходного процесса 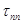, вычисленные по уравнению для динамической ошибки системы при x>1 и D=0,1.

x		1,1	1,2	1,3	1,4	1,5	2,0
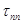
	3,89	4,4	4,92	5,44	5,95	6,47	8,85

Действительная длительность переходного процесса равна найденному из таблицы значению 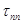, деленному на w₀.

Рис.. Формы переходных процессов

кривая при x>1; 2.— кривая при x=1; 3 — кривая при x<1.

9.3.2 Корни равны друг другу (р₁ = р₂).

Этот случай соответствует x=1. При этом корни: р₁ = р₂ = -w₀.

Переходная функция при подаче ступенчатого воздействия имеет вид:

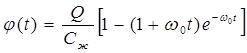
Установившееся значение j(t) определяется при t = ¥:

Разделив j(t) на j(¥) получим безразмерную переходную функцию:

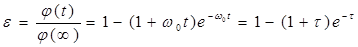
где t = w₀t – безразмерное время.

Переходный процесс 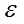= f(t) также является апериодическим (кривая 2 на рис.).

Динамическая ошибка: D = 1- e = (1+ t)е^-t.

9.3.3 Корни характеристического уравнения неравные и комплексные (р₁¹р₂, x<1)

В этом случае существует некоторое оптимальное значение x, при котором длительность переходного процесса получается минимальной.

Корни характеристического уравнения в данном случае равны:

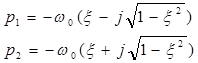
Если подставить эти выражения в уравнение переходной функции (24) и совершить переход от комплексных выражений к тригонометрическим, можно получить переходную функцию в виде:

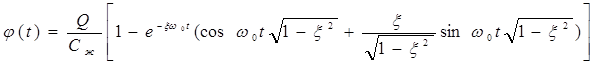(25)

Переходные процессы при x<1 имеют колебательный характер.

Из последнего уравнения определяются основные показатели переходного процесса.

Круговая частота колебаний демпфированной системы:

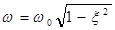
При x = 0 система является недемпфированной, при этом . Следовательно, параметр w₀ представляет собой недемпфированную частоту собственных колебаний. С увеличением x частота w уменьшается от w = w₀ (при x = 0) до w = 0 (при x=1).

Частота колебаний в Герцах:

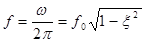, где .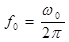

Период колебаний:

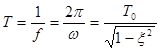
где T₀ = 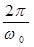– период колебаний недемпфированной системы. С увеличением x период T увеличивается, стремясь к ¥ при x = 1.

Декремент затухания d, равный отношению абсолютных значений двух максимальных отклонений за два последовательных полупериода:

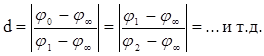(26)

где j₀, j₁, j₂ и j_¥ - значения функции соответственно при t = 0, t = T/2, t = T, t = ¥.

Подставляя последовательно в уравнение (25) значения t = 0, t = T/2 и t = ¥ находим:

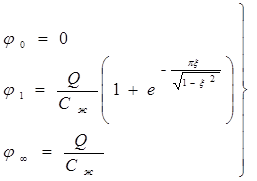(27)

Подставляя (27) в (26) определим декремент затухания:

,

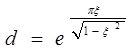иногда пользуются обратной величиной 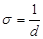— это есть перерегулирование, оно определяет относительную величину разности между первым максимумом переходного процесса и его установившимся значением:

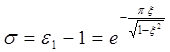(28)

Логарифмический декремент затухания:

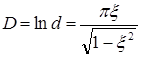. (29)

По формулам (28) и (29) вычислены d, s, D, которые сведены в таблицу:

x		0,1	0,2	0,3	0,4	0,5	0,6	0,7	0,8	0,9
d		1,37	1,89	2,68	3,94	6,14	10,5	21,7
s		0,73	0,53	0,37	0,25	0,16	0,09	0,046	0,015	0,0015
D		0,32	0,64	0,98	1,37	1,82	2,35	3,08	4,18	6,49

При колебательном процессе аналитическое определение безразмерной длительности переходного процесса t_пп не представляется возможным т.к. кривая переходного процесса пересекает зону допустимых динамических ошибок ±D несколько раз и поэтому t_пп приходится определять графически (кривая 3 на рисунке).

Действительная длительность переходного процесса равна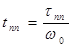

Следовательно, увеличение собственной частоты не демпфированных колебаний приводит к уменьшению длительности переходного процесса.

Дата добавления: 2014-12-07