Частотные характеристики звеньев

Частотные характеристики определяют динамические свойства звеньев при воздействии на них гармонических сигналов. формально частотные характеристики получаются из передаточной функции W (s) при , где
– угловая частота, имеющая размерность [рад/с]. Сделав такую замену, получим

(2.13)

т.е. частотная передаточная функция есть прямое преобразование Фурье от весовой функции w (t).

Комплекснозначную функцию частоты будем называть амплитудно-фазовой частотной xаpактepистикой (АФЧХ) звена.

Как любое комплексное число АФЧХ можно представить в виде

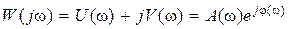, (2.14)

где

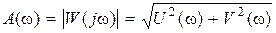, (2.15)

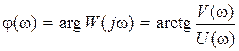. (2.16)

Если передаточная функция звена представлена в виде , то . При этом, очевидно, (считаем 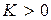) и .

В соответствии с (2.14)–(2.16) имеем еще ряд частотных характеристик: 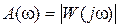– амплитудно-частотная xаpактepистика (АЧХ); – фазово-частотная xаpактepистика (ФЧХ); 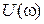, 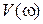– соответственно вeществeнная и мнимая частотные характеристики.

Рассмотрим физический смысл частотных характеристик. Если на вход звена с передаточной функцией W (s) поступает гармонический сигнал , то в установившемся режиме после затухания переходной составляющей выходной сигнал будет также гармоническим: , т.е. той же частоты, но измененных амплитуды и фазы.

Изменение амплитуды определяется модулем , а фазы – аргументом на соответствующей частоте .

На практике для наглядности частотные характеристики изображают в виде графиков при изменении частоты 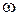от 0 до .

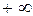Частотные характеристики обладают следующими свойствами: 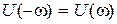, , 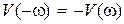, , 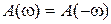которые непосредственно следуют из (2.14)–(2.16). Другими словами: характеристики 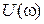, 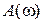являются четными, 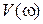, 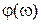– нечетными. В силу этого графики при изменении частоты oт –∞ до 0 не строятся. АФЧХ представляет собой годограф на комплексной плоскости с координатами u, v или А, 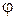при изменении 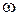от 0 до .

На рис. 2.4 и 2.5 представлены иллюстративные графики частотных характеристик некоторого звена.

Рис. 2.4

Штриховой линией показаны части графиков, соответствующие . Вполне понятно, что из графика (см. рис. 2.4) нетрудно получить графики а, б или соответственно в, г (см. рис. 2.5) и наоборот.

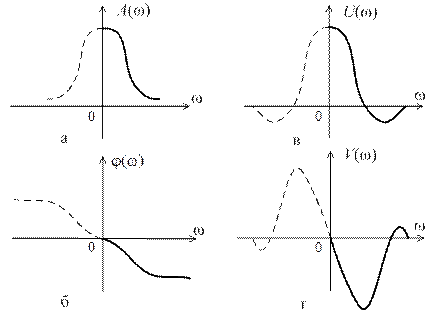
Рис. 2.5

На практике часто применяются соответствующие логарифмические частотные характеристики: логаpифмичeская амплитудная частотная характеристика (ЛАЧХ) 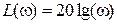и логарифмическая фазовая частотная xаpактepистика (ЛФЧХ) 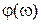, графики которых строятся в логарифмическом масштабе. При построении по оси ординат откладывается величина , единицей измерения которой является децибел, а по оси абсцисс –
частота 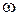[1/с] в логарифмическом масштабе, т.е. величина . Увеличение 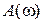в 10 раз соответствует приращению вдоль оси ординат на 20 дБ. При построении ЛФЧХ величину 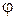откладывают по оси ординат в обычном масштабе (в градусах или радианах), a 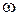– в логарифмическом масштабе.

На рис. 2.6 приведены иллюстративные графики ЛАЧХ и ЛФЧХ для некоторого звена. Частота 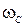, при которой 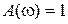,носит название частоты среза. Левее 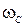значения 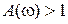(усиление), правее – 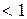(ослабление амплитуды гармонического сигнала).

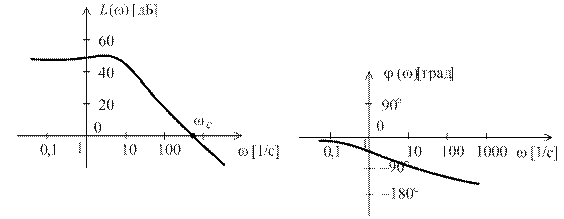
Рис. 2.6

Дата добавления: 2014-12-07