Элементы комбинаторики. 3 страница

Найдем дисперсию равномерно распределенной случайной величины.

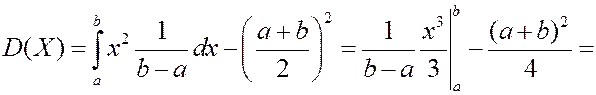
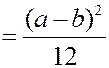
Показательное распределение.

Распределение называется показательным, если плотность вероятности представляется показательной функцией.

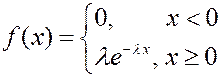
Найдем математическое ожидание случайной величины, распределенной по показательному закону.

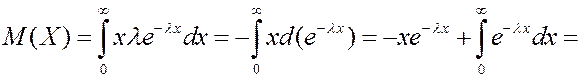
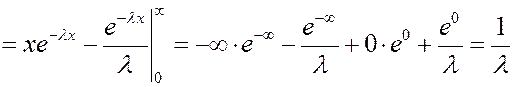
Дисперсию случайной величины найдем аналогично.

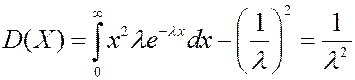
Нормальное распределение.

Случайная величина распределена нормально, если плотность вероятности представляется в ви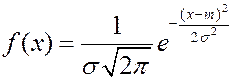де.

, где 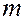- математическое ожидание, а - среднее квадратичное отклонение.

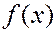
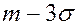
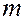
Вероятность попадания величины, распределенной нормально, на заданный промежуток вычисляется по формуле

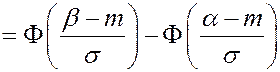
Пример. Мат. ожидание нормально распределенной случайной величины равно 10, а дисперсия 4. Записать плотность вероятности и вычислить вероятность попадания на интервал (12, 14).

Решение.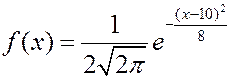

Правило “трех сигм”.

Найдем вероятность отклонения нормально распределенной СВ от своего математического ожидания.

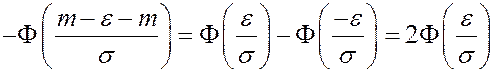
Обозначим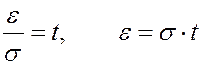

При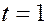

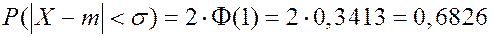
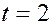
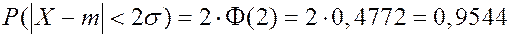
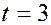
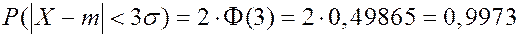
Если СВ распределена нормально, то отклонение СВ от математического ожидания с вероятностью 0,9973 не превосходит утроенного среднего квадратического отклонения.

Математическая

статистика.

Математическая статистика – наука, занимающаяся разработкой методов получения, описания, обработки опытных данных с целью изучения закономерностей случайных явлений.

Основные задачи.

1. На основе опытных данных найти закон распределения случайной величины.

2. На основе опытных данных найти параметры функции распределения.

3. Установить насколько согласуется предполагаемая функция распределения с истинной функцией.

Генеральная совокупность – совокупность объектов, свойства которых нужно изучить.

Выборочная совокупность – совокупность объектов отобранных из генеральной совокупности для исследования.

Повторная выборка – выборка, в которой каждый выбранный из генеральной совокупности элемент возвращается в генеральную совокупность перед выбором следующего элемента.

Бесповторная выборка – выборка, в которой каждый выбранный из генеральной совокупности элемент не возвращается.

Репрезентативность (представительность) выборки – свойство выборки правильно отражать закономерности генеральной совокупности.

Статистический ряд.

Пусть - случайная величина.

Задача: указать определенные признаки случайной величины. Ставится эксперимент, и результаты записываются в виде таблицы.

Номер опыта			…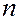
Значение СВ			…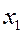

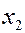
Объем выборки – число проведенных экспериментов. Объем выборки равен .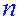

Необходимо упорядочить значение СВ (обычно по возрастанию) и подсчитать сколько раз встречается то или иное значение.

Значение СВ.			…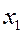
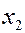
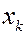
Частота			…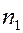

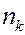
Частота равна числу экспериментов, в которых СВ приняла значение .

Сумма частот равна объему выборки.

Полигон частот – ломаная линия с вершинами в точках 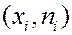. Это графическое изображение результатов эксперимента.

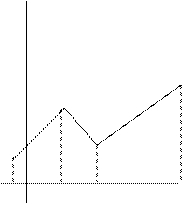
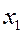
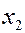
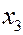
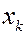
Статистическая функция распределения 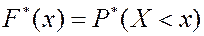- закон, описывающий вероятность частоты неравенства . Для получения статистической функции распределения необходимо подсчитать число опытов, где и разделить на объем выборки.

Для описания результатов опыта используется также относительная частота , равная отношению частоты к объему выборки.

Значение СВ.			…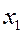
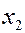
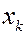
Относит. частота			…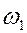

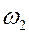
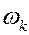
Сумма относительных частот равна единице.

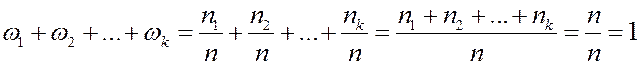Если число опытов велико и запись в виде статистического ряда затруднена, то используется статистическая совокупность – группы, на которые разбиваются результаты наблюдений.

Пример. Статистическая совокупность ошибок 100 измерений дальности.

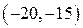
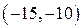
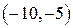
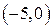
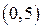
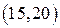
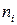
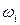
	0,02	0,08	0,17	0,24	0,26	0,13	0,06	0,04

Гистограмма – геометрическое изображение статистической совокупности. На оси абсцисс откладываются отрезки, соответствующие группам, на которые разбиты данные. На каждом отрезке строится прямоугольник, площадь которого равна частоте (или относительной частоте).

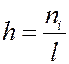или

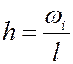
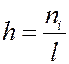
20

Начертив гистограмму для относительной частоты, получим первое приближение для плотности вероятности.

Числовые характеристики.

Среднее выборочное – среднее арифметическое всех значений случайной величины, полученных в результате опытов.

Если выборка повторная, то есть значениям случайной величины соответствует некоторая частота, среднее выборочное вычисляем с учетом частот.

Выборочная дисперсия – среднее арифметическое квадратов отклонения значений случайной величины от среднего выборочного:

.

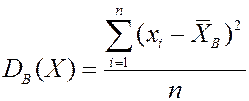Либо по более удобной формуле:

.

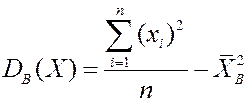С учетом частот можем вычислить дисперсию следующим образом.

Задача. Для оценки покупательского спроса в отделе мужской обуви проведена регистрация размеров обуви в порядке покупки. Получены следующие результаты.

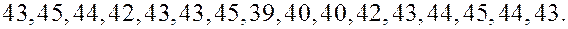
Объем выборки равен .

Найдем среднее выборочное.

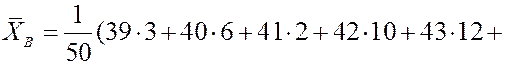
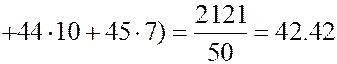
Найдем выборочную дисперсию.

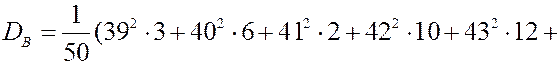
Свойства точечных оценок.

Пусть распределение СВ зависит от неизвестного параметра 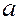. На основании опытных данных находим приближенное значение параметра 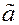- оценка параметра.

Оценка параметра 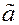- случайная величина, её значение зависит от того, какие значения принимает случайная величина , то есть от закона распределения СВ и числа опытов.

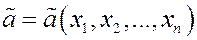
Для того, чтобы 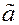имела практическую ценность, она должна удовлетворять ряду требований.

1. Несмещенность.

Оценка 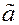несмещенная, если мат. ожидание от оценки параметра равно самому параметру.

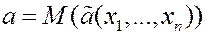
2. Состоятельность.

Оценка 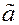состоятельна, если сходится по вероятности к параметру .

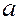3. Эффективность.

Необходимо выбрать оценку, у которой дисперсия наименьшая. Чем меньше дисперсия, тем меньше вероятность грубой ошибки.

Оценка математического ожидания и дисперсии.

Оценкой мат. ожидания является выборочное среднее.

В качестве оценки для дисперсии рассмотрим статистическую дисперсию.

Статистическая дисперсия является смещенной оценкой дисперсии. Тогда, в качестве оценки выберем следующую величину.

Эту оценку называют исправленной дисперсией и обозначают .

Задача. Вычислим исправленную дисперсию в предыдущей задаче.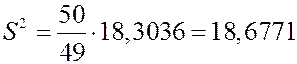

Интервальные оценки.

Необходимо определить точность и надежность полученной оценки. Зададим достаточно большую вероятность 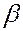(0.9, 0.95, 0.99), которая называется доверительной вероятностью. Построим доверительный интервал – интервал, который с вероятностью 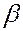накроет искомый параметр.

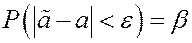
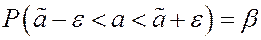
Построим доверительный интервал для математического ожидания.

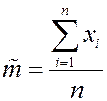
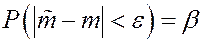
Если 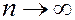, то по теореме Ляпунова случайная величина подчиняется нормальному распределению.

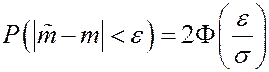
Тогда 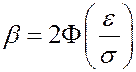. Найдем из этого равенства.

, ,

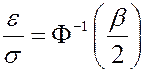Среднее квадратичное отклонение находим таким образом.

Таким образом, доверительный интервал для математического ожидания представим в виде.

Здесь 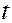- это корень уравнения .

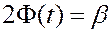Задача. Найти доверительный интервал для оценки с надежностью 0.95 мат. ожидания 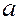нормально распределенного признака, если среднее выборочное равно 14, объем выборки 25, среднее квадратичное отклонение 5.

Решение.

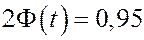
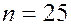
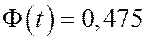
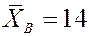
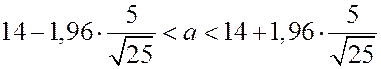
Проверка гипотез.

Пусть из генеральной совокупности получена некоторая выборка. Анализируя эту выборку, мы предполагаем, что генеральная совокупность может обладать некоторым свойством (выдвигаем гипотезу). Так как мы не имеем возможности анализировать генеральную совокупность, мы можем сделать ошибку. Допустим, что генеральная совокупность имеет некоторое свойство, а мы утверждаем, что такого свойства нет. Отказ от гипотезы в случае, когда она на самом деле верна, называется ошибкой первого рода. Наоборот, если генеральная совокупность не имеет некоторого свойства, а мы утверждаем, что такое свойство есть, то мы принимаем неверную гипотезу. Это называется ошибкой второго рода.

Вероятности ошибок первого и второго рода не равны 0. Вероятность ошибки первого рода называется уровнем значимости. При построении методов проверки гипотез стараются, чтобы она была не очень большой (0,1; 0,05; 0,01). Вероятность, что не будет допущена ошибка второго рода, называется мощностью критерия.

Проверка гипотезы о нормальном распределении

генеральной совокупности по критерию Пирсона.

Пусть мы получили выборку, по виду которой мы имеем основание предполагать, что случайная величина распределена нормально.

По выборке вычислим 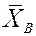и . Сформулируем гипотезу: случайная величина распределена нормально и зависит от параметров 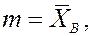. Для проверки этой гипотезы вычислим, какие частоты должна иметь нормально распределенная случайная величина.

Теоретические частоты .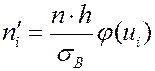

Здесь 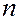- объем выборки, - шаг, , .

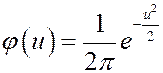Для оценки насколько частоты, полученные в выборке, отличаются от теоретических частот, найдем следующую величину.

Теперь, необходимо сравнить с критическим значением 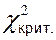, которое зависит от уровня значимости 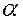и числа степеней свободы 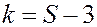, где - число групп выборки.

Если 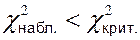, то гипотеза о нормальном распределении принимается.

Если , то гипотеза о нормальном распределении отвергается.

Задача. Проверить на уровне значимости гипотезу о нормальном распределении генеральной совокупности, если получена следующая выборка.

	0,3	0,5	0,7	0,9	1,1	1,3	1,5	1,7	1,9	2,1	2,3

Решение.

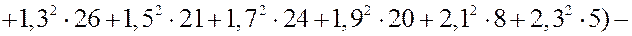
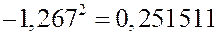
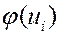
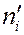
0,3	-1,934	0,0610	4,88
0,5	-1,534	0,1230	9,84
0,7	-1,134	0,2100	16,8
0,9	-0,734	0,3050	24,4
1,1	-0,334	0,3775	30,2
1,3	0,066	0,3981	31,848
1,5	0,466	0,3585	28,68
1,7	0,866	0,2750
1,9	1,266	0,1800	14,4
2,1	1,666	0,1000
2,3	2,066	0,0472	3,776

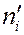
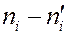
	4,88	1,12	1,2544	0,257
	9,84	-0,84	0,7056	0,072
	16,8	9,2	84,64	5,038
	24,4	0,6	0,36	0,015
	30,2	-0,2	0,04	0,0013
	31,848	-5,848	34,199	1,074
	28,68	-7,68	58,98	2,056
				0,182
	14,4	5,6	31,36	2,178
	3,776	1,224	1,498	0,397

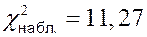
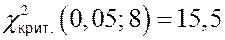
Гипотеза о нормальном распределении генеральной средней принимается, так как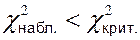

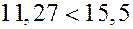
Корреляция. Линии регрессии.

Предположим, что мы изучаем одновременно две случайные величины 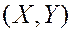. Пусть в результате испытания нами получено 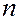точек 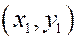, , , , 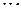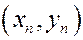среди которых могут быть и совпавшие. Вопрос: зависят ли эти две случайные величины друг от друга, и, если зависят, то каков характер этой зависимости.

Дата добавления: 2014-12-07