Нормализация случайных величин

Не нарушая общности законов распределений задачи нормализация случайных величин будем решать применительно к стандартному нормальному распределению. Постановка задачи заключается в следующем.

Если случайная величина 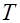имеет закон распределения , то необходимо исходную случайную величину 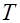подвергнуть такому преобразованию ,

в результате которого случайная величина 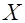имела бы плотность гауссова распределения.

Основной результат решения этой задачи можно сформулировать в виде следующего утверждения

Теорема 7. Пусть – функция распределения случайной величины 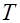, тогда для нее существует нормализующее преобразование вида

, (29)

где являются коэффициентами разложения в ряд квантили стандартного нормального распределения.

Доказательство. Если уравнение (30)

однозначно разрешимо относительно 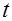, то применив инверсный оператор к обеим частям уравнения (30), получим

. (31)

Квантиль (31) определяется следующим соотношением

. (32)

где ; .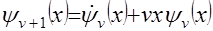

Следовательно, явное выражение для нормализующего преобразования приобретает вид (29).

Значения коэффициентов , вычисленные по рекуррентной формуле (29), представлены в табл. 2.

В условиях малых выборок постановка задач нормализации случайных величин заключается в следующем.

Случайные величины 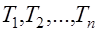независимы и одинаково распределены с общей неизвестной функцией распределения и эту выборку правомерно рассматривать как одну из целой совокупности выборок, которая может быть осуществлена путем вторичного извлечения случайных выборок того же объёма из данной генеральной совокупности. Изменяющимся случайным образом от выборки к выборке случайным величинам соответствует эмпирическое выборочное распределение.

Эмпирическая функция распределения 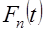представляет собой ступенчатую функцию со скачками, кратными в точках, определяемых членами вариационного ряда 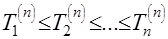, 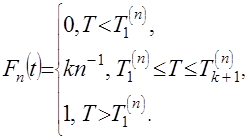(33)

Таблица 2. Значения коэффициентов

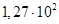
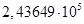
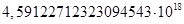
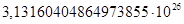
По закону больших чисел при 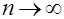для какого 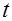эмпирическая функция сходятся по вероятностям к исходному теоретическому распределению .

Это обстоятельство дает возможность непосредственно применить теорему 7 для нормализации случайных величин

. (34)

Представление функции квантилей в виде ряда (системы уравнения относительно коэффициентов ) (35)

позволяет определить коэффициенты разложение нормализующего преобразования (29) после решения системы уравнений (35) для выборочных значений при следующим образом

,

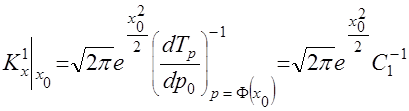и т.д.

Дата добавления: 2014-12-07