
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Розв’язання тригонометричних рівнянь
|
|
|
|
Розв’язання найпростіших тригонометричних рівнянь
Рівняння називаються тригонометричними, якщо невідома величина знаходиться під знаком тригонометричних функцій. Найпростішими тригонометричними рівняннями називаються рівняння  ,
,  ,
, 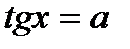 ,
,  . Розв’язати найпростіше тригонометричне рівняння – означає знайти множину всіх кутів, що мають дане значення
. Розв’язати найпростіше тригонометричне рівняння – означає знайти множину всіх кутів, що мають дане значення 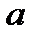 тригонометричної функції.
тригонометричної функції.
Розглянемо розв’язання найпростіших тригонометричних рівнянь:
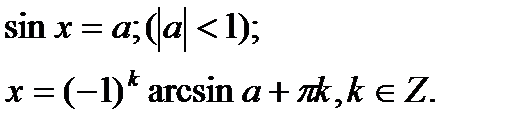
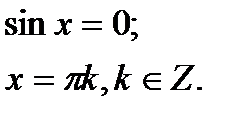


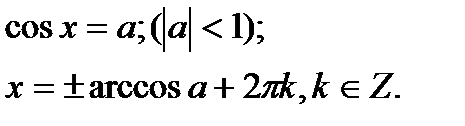

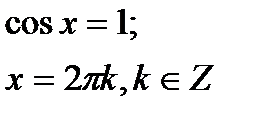



55. Розв’яжіть рівняння:
1)  ; 2)
; 2)  ;
;
3)  ; 4)
; 4) 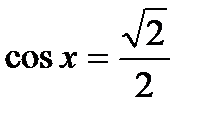 ;
;
5) 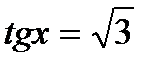 ; 6)
; 6) 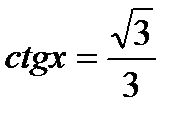 ;
;
7)  ; 8)
; 8)  ;
;
9)  ; 10)
; 10)  ;
;
11) 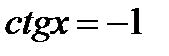 ; 12)
; 12)  .
.
56. Розв’яжіть рівняння:
1)  ; 2)
; 2)  ;
;
3)  ; 4)
; 4)  ;
;
5) 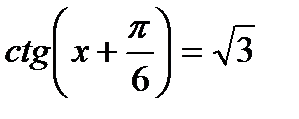 ; 6)
; 6) 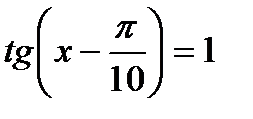 ;
;
7) 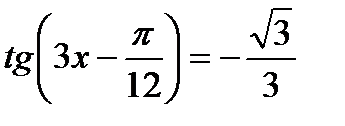 ; 8)
; 8)  ;
;
9) 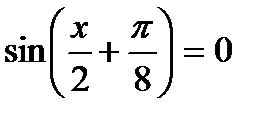 ; 10)
; 10) 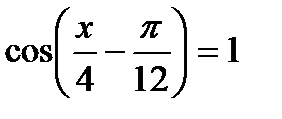 ;
;
11) 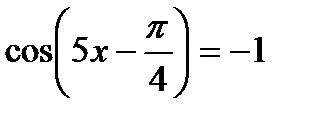 ; 12)
; 12) 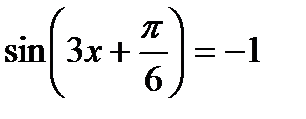 ;
;
57. Розв’яжіть рівняння:
1)  ; 2)
; 2) 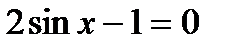 ;
;
3) 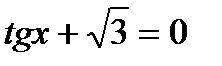 ; 4)
; 4) 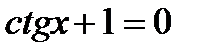 ;
;
5)  ; 6)
; 6)  ;
;
7)  ; 8)
; 8)  ;
;
9)  ; 10)
; 10)  ;
;
11)  ; 12)
; 12) 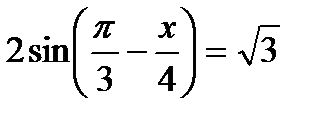 ;
;
13)  ; 14)
; 14)  ;
;
15) 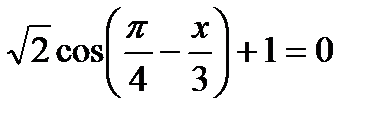 ; 16)
; 16)  ;
;
17)  ; 18)
; 18)  ;
;
19) 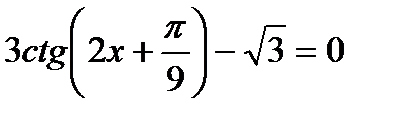 ; 20)
; 20) 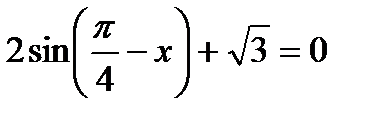 .
.
58. Розв’яжіть рівняння:
1)  ; 2)
; 2) 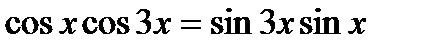 ;
;
3) 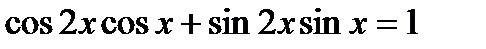 ; 4)
; 4)  ;
;
5) 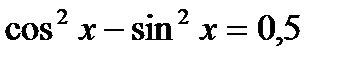 ; 6)
; 6) 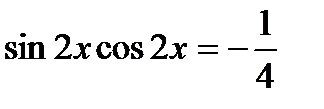 ;
;
7) 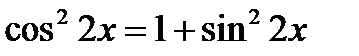 ; 8)
; 8)  ;
;
9) 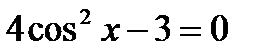 ; 10)
; 10)  ;
;
11)  ; 12)
; 12)  ;
;
13) 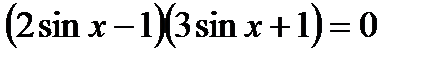 ; 14)
; 14) 
до змісту
Якщо тригонометричне рівняння не є найпростішим, то за допомогою тотожних перетворень його треба звести до одного або кількох найпростіших, розв’язання яких визначається стандартними формулами.
Деякі тригонометричні рівняння шляхом тотожних перетворень можна привести до рівняння з однією тригонометричною функцією, потім зробити заміну і привести рівняння до квадратного.
Приклад 1. Розв’язати рівняння 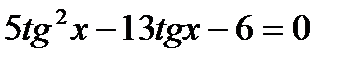 .
.
Розв’язання
Нехай 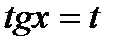 , тоді
, тоді 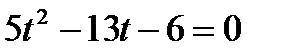 .
.
Звідси 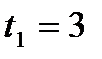 ,
, 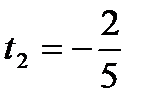 .
.
Оскільки  , то
, то 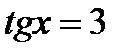 ,
, 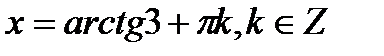 .
.
Оскільки 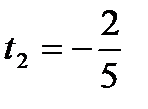 , то
, то  ,
, 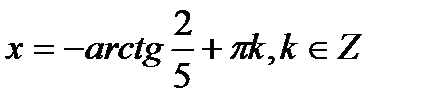 .
.
Відповідь:  ;
;  ;
;  .
.
Приклад 2. Розв’язати рівняння 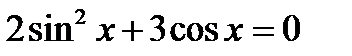 .
.
Розв’язання
Замінивши  на
на  , матимемо:
, матимемо:
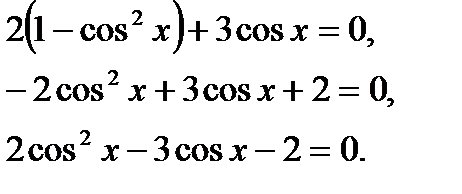
Нехай  , тоді
, тоді 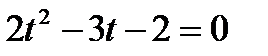 .
.
Звідси  ,
, 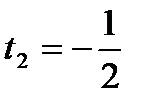 .
.
Оскільки 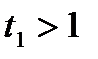 , то рівняння
, то рівняння  розв’язків немає.
розв’язків немає.
Оскільки  , то
, то 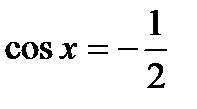 ,
, 
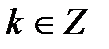
Отже 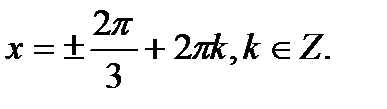
Відповідь: 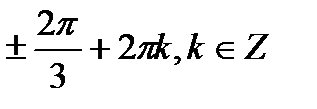
Приклад 3. Розв’язати рівняння  ,
,
Розв’язання
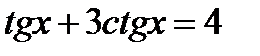 ,
, 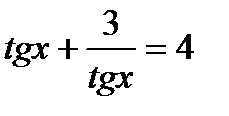 .
.
Нехай  , тоді
, тоді 
 ,
, 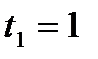 ,
, 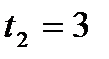 .
.
Маємо: 1) 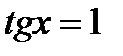 ,
, 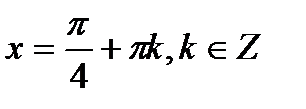 .
.
2) 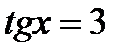 ,
, 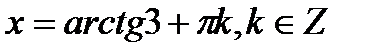 .
.
Відповідь: 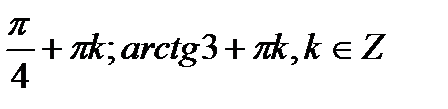 .
.
59. Розв’яжіть рівняння:
1) 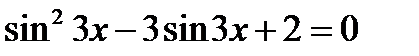 , 2)
, 2) 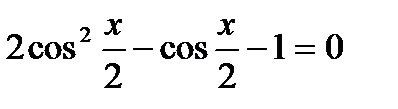 ,
,
3)  , 4)
, 4) 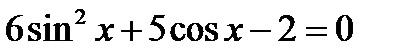 ,
,
5) 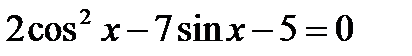 , 6)
, 6)  ,
,
7) 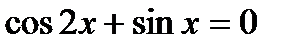 , 8)
, 8)  ,
,
9) 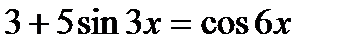 , 10)
, 10) 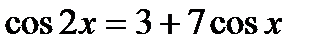 ,
,
11) 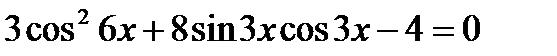 , 12)
, 12) 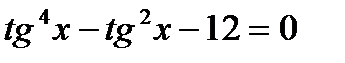 .
.
13)  , 14)
, 14)  ,
,
15) 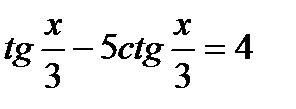 , 16)
, 16) 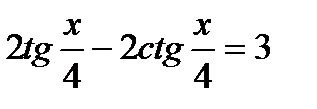 .
.
Багато тригонометричних рівнянь, права частина яких дорівнює 0, розв’язуються розкладанням їхньої лівої частини на множники.
|
|
|
Приклад 1. Розв’язати рівняння  .
.
Розв’язання
Врахувавши, що  , матимемо:
, матимемо:
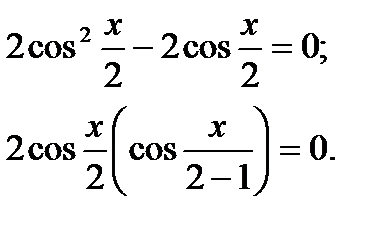
Добуток дорівнює нулю, якщо хоча б один із множників дорівнює нулю. Тому:
1) 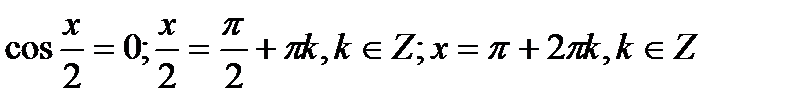 .
.
2)  .
.
Відповідь: 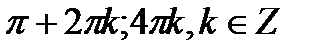 .
.
Приклад 2. Розв’язати рівняння 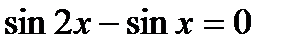 .
.
Розв’язання

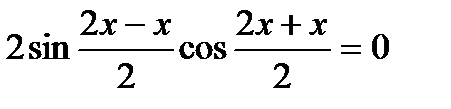 ;
;
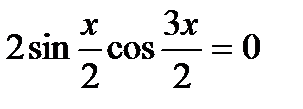 .
.
1)  .
.
2) 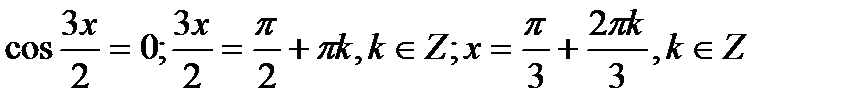 .
.
Відповідь:  .
.
60. Розв’яжіть рівняння:
1) 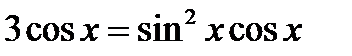 , 2)
, 2) 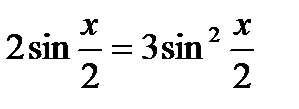 ,
,
3) 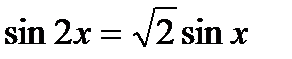 , 4)
, 4)  ,
,
5)  , 6)
, 6) 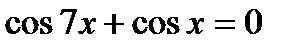 ,
,
7)  , 8)
, 8) 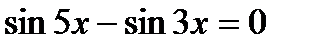 ,
,
9) 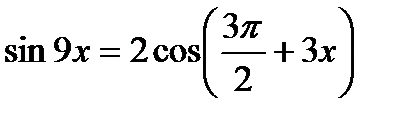 , 10)
, 10)  ,
,
11)  , 12)
, 12)  ,
,
13) 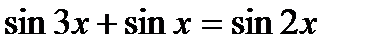 , 14)
, 14) 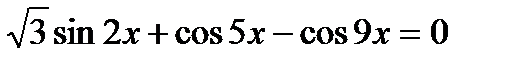 ,
,
15) 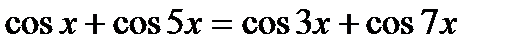 , 16)
, 16) 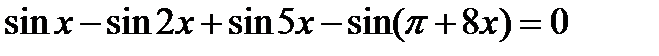 .
.
Рівняння виду 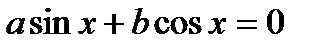 , де
, де 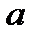 і
і  не дорівнюють нулю, називається однорідним рівнянням 1-го степеня.
не дорівнюють нулю, називається однорідним рівнянням 1-го степеня.
Значення  , при яких
, при яких  дорівнює нулю, не задовольняє даному рівнянню, бо тоді і
дорівнює нулю, не задовольняє даному рівнянню, бо тоді і  теж дорівнював би нулю. Тому можна розділити обидві частини рівняння на
теж дорівнював би нулю. Тому можна розділити обидві частини рівняння на  . Маємо:
. Маємо:
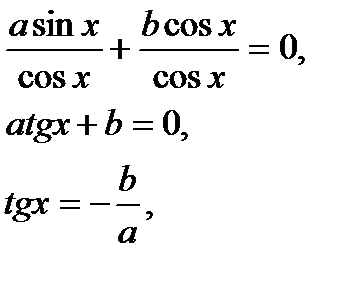

Рівняння виду: 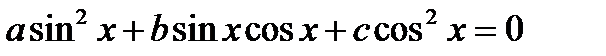 називається однорідним рівнянням 2-го степеня.
називається однорідним рівнянням 2-го степеня.
Якщо числа 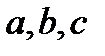 не дорівнюють нулю, то розділимо дане рівняння на
не дорівнюють нулю, то розділимо дане рівняння на  (або на
(або на 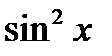 ). У даному рівнянні
). У даному рівнянні  , бо в супротивному випадку
, бо в супротивному випадку 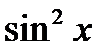 теж дорівнював би нулю. Тоді
теж дорівнював би нулю. Тоді

61. Розв’яжіть рівняння:
1) 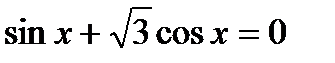 , 2)
, 2)  ,
,
3) 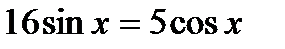 , 4)
, 4) 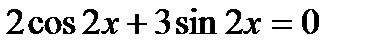 ,
,
5) 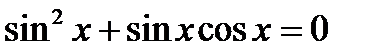 , 6)
, 6) 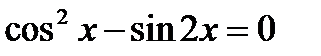 ,
,
7)  , 8)
, 8) 
9)  , 10)
, 10) 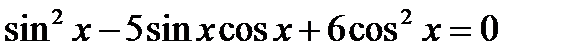 ,
,
11)  , 12)
, 12) 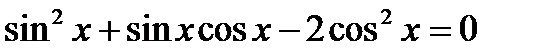 ,
,
13)  , 14)
, 14) 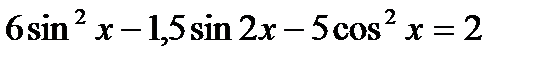 .
.
62. Розв’яжіть рівняння
1) 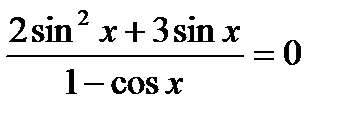 ; 2)
; 2) 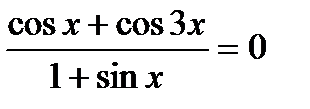 ;
;
3) 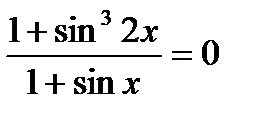 ; 4)
; 4) 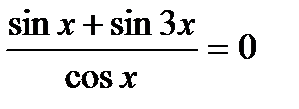 ;
;
5)  ; 6)
; 6)  ;
;
7)  ; 8)
; 8) 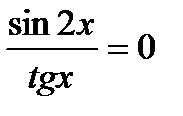 .
.
до змісту
§ 11 Розв’язання тригонометричних нерівностей
Тригонометричними нерівностями називаються нерівності, у яких змінна знаходиться під знаком тригонометричної функції.
 Рис. 6
Рис. 6
Таблиця 3

| 
| 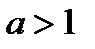
| |
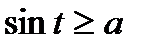
| 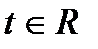
|  
| Розв’язків немає |
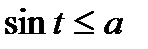
| Розв’язків немає | 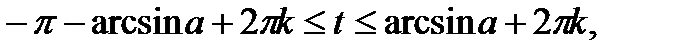 
| 
|
 Рис. 7
Рис. 7
Таблиця 4

| 
| 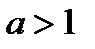
| |

| 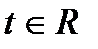
| 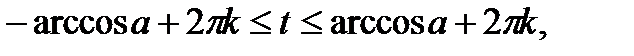 
| Розв’язків немає |
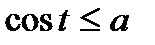
| Розв’язків немає |  
| 
|
Таблиця 5
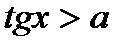
|  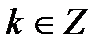
|

| 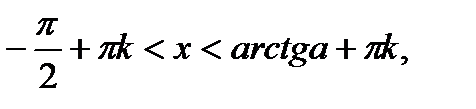 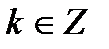
|

|  
|
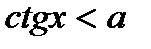
| 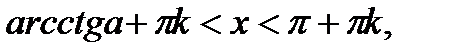 
|
63. Розв’яжіть нерівність:
1) 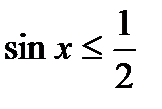 , 2)
, 2)  ,
,
3)  , 4)
, 4) 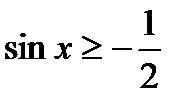 ,
,
5) 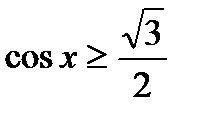 , 6)
, 6)  ,
,
7) 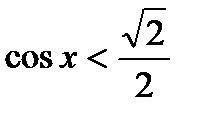 , 8)
, 8)  ,
,
9)  , 10)
, 10) 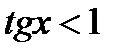 ,
,
11)  , 12)
, 12)  ,
,
13) 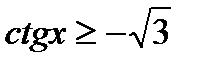 , 14)
, 14)  ,
,
15)  , 16)
, 16) 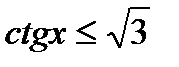 .
.
64. Розв’яжіть нерівність:
1)  , 2)
, 2)  ,
,
3) 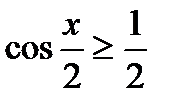 , 4)
, 4)  ,
,
5) 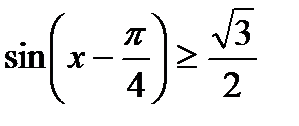 , 6)
, 6) 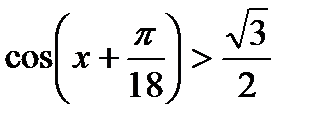 ,
,
7) 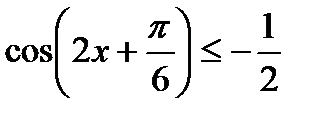 , 8)
, 8) 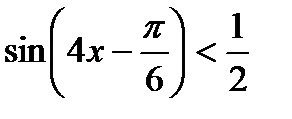 ,
,
9)  , 10)
, 10) 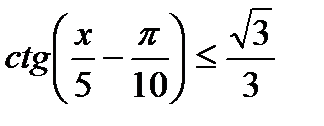 ,
,
11)  , 12)
, 12)  .
.
65. Розв’яжіть нерівність:
1)  , 2)
, 2) 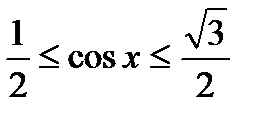 ,
,
3) 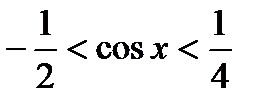 , 4)
, 4) 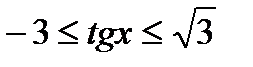 ,
,
5)  , 6)
, 6)  ,
,
7)  , 8)
, 8) 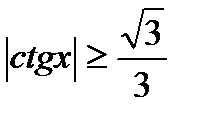 .
.
66. Розв’яжіть нерівність:
1) 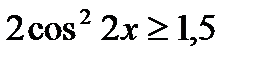 , 2)
, 2) 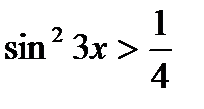 ,
,
3) 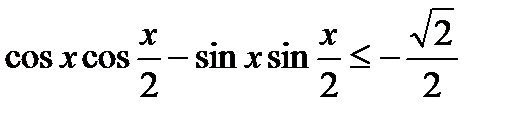 , 4)
, 4)  ,
,
5)  , 6)
, 6)  ,
,
7) 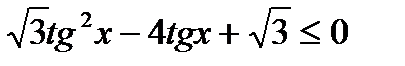 , 8)
, 8)  .
.
до змісту
|
|
|
|
|
Дата добавления: 2014-11-29; Просмотров: 822; Нарушение авторских прав?; Мы поможем в написании вашей работы!